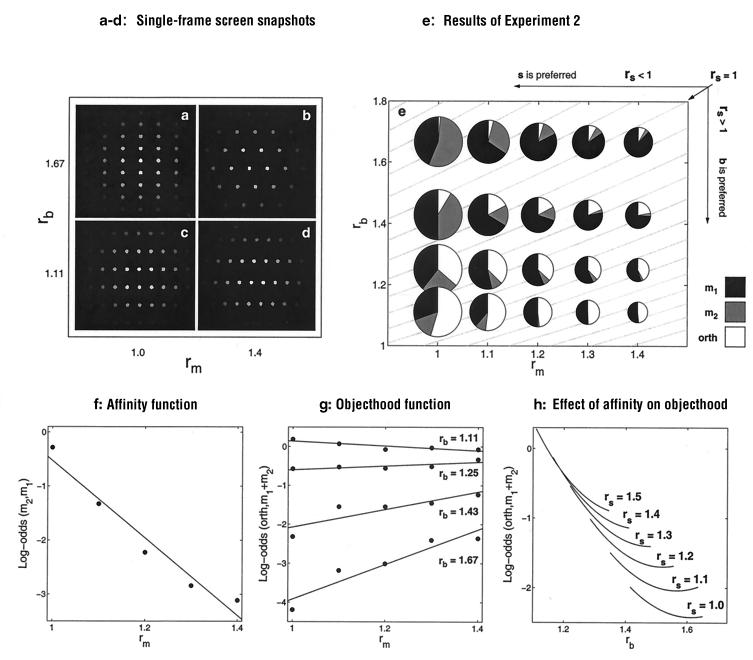
Figure 4.

(a–d) Single frames captured from the computer screen with the extreme values of r_m = (|m₂|/|m₁|) and r_b = (|b|)/|m₁|). The snapshots are arranged in the (r_m, r_b) space, parallel to the plot in e. (e) The pie charts show the distribution of the three responses in the 20 motion lattices. The gray lines on the background are the iso-r_s lines, where r_s = (|s|/|b|), which are the contours for which within-frame spatial grouping should remain constant. For the isoline r_s = 1.0, the organizations along s and b are equiprobable. It is marked with an oblique arrow (Upper Right). Conditions that favor dot grouping within the baselines (r_s > 1.0; e.g., c and d) lie to the right of the isoline of r_s = 1.0; in the rest of the conditions (r_s < 1.0), dots tend to form groupings not along the baselines (as in a). (f) Affinity function collapsed across the r_b conditions. (g) Four objecthood functions summarize the effects of the baseline and motion ratios, r_b and r_m. The frequency of g-motion grows rapidly as r_b drops and groupings along the baselines become more prominent. This effect is evident both when r_b is low (high ambiguity of e-motion) and when r_b is high (m₁ wins the competition with m₂). The plot in h explicates the effect of r_s. Dot organizations within the baselines dissolve as r_s grows, which reduces the frequency of g-motion. In contrast to the prediction of the sequential model, e-motion and g-motion tradeoff within the iso-r_s sets.