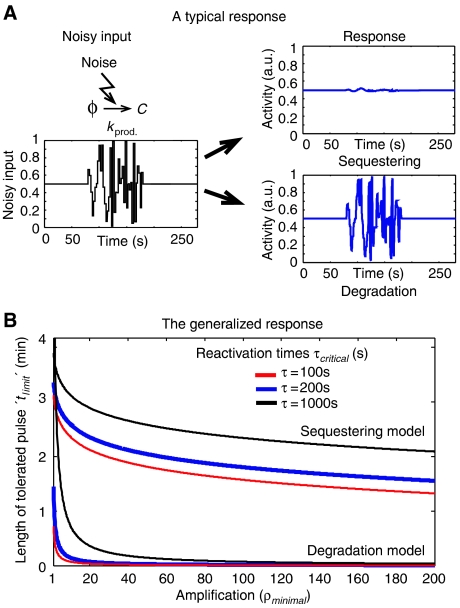
Figure 2.

Noise resistance. (A) A typical response to noise: The two models were exposed to the identical noisy input shown, and their dynamics was followed. We note that the sequestering-based model is much more resistant to noise than the degradation-based model. A frequency–response analysis of this system was also performed, which confirmed these results (see Supplementary information). Parameters used: Degradation model: k_prod.=1 M s⁻¹, k_deg.^on=0.1 M s⁻¹ and k_deg.^on=1 s⁻¹. Sequestering model: k_prod.=0.01 M s⁻¹, k_deg.=0.01 s⁻¹, k_ass.∼0.01 M s⁻¹ and k_diss.∼0.1 M s⁻¹. Both models: m_tot.=10, k_m=1 s⁻¹and k_−m=100 s⁻¹. (B) In order to compare the two models, we defined a noise resistance threshold corresponding to the time, ‘t_limit', it takes for either model to reach a fraction of 1−e⁻¹ of the difference between its initial and final value. The larger t_limit, the longer time it takes for the system to reach its final steady-state value. t_limit is thus a measure of how long perturbations the system can handle. In the figure, we see how the critical time varies with the amplification and reactivation time. The fact that the sequestering-based model is able to buffer longer perturbations is clearly seen. Worth noting is also that the vertical location of the sequestering curve depends on the free parameter k_deg., the current value was thus chosen as an example rather than as an absolute value. Parameter used: degradation model — k_prod.=1 M s⁻¹, k_deg.^on=0.1 M s⁻¹ and k_deg.^on=1 s⁻¹; storage model — k_prod.=0.01 M s⁻¹, k_deg.=0.05 s⁻¹ and k_ass.∼0.1 M s⁻¹; both models—m_tot.=10, k_m=1 s⁻¹and k_−m=100 s⁻¹.