SPA: simple web tool to assess statistical significance of DNA patterns

Abstract

Many statistical methods and programs are available to compute the significance of a given DNA pattern in a genome sequence. In this paper, after outlining the mathematical background of this problem, we present SPA (Statistic for PAtterns), an expert system with a simple web interface designed to be applied to two of these methods (large deviation approximations and exact computations using simple recurrences). A few results are presented, leading to a comparison between the two methods and to a simple decision rule in the choice of that to be used. Finally, future developments of SPA are discussed. This tool is available at the following address: http://stat.genopole.cnrs.fr/SPA/.

INTRODUCTION

Since the appearance of large scale genome sequencing projects, automatic extraction of biologically meaningful information has become a key issue in genetic research. One way to assess the functional role of an oligomer would be to evaluate its degree of significance with respect to a random sequence model. Markov chain models of order m, preserving counts of m+1 letter words, and thus modelling neighbouring letter interactions, have been extensively used in the study of biological sequences (1,2). For example, under-represented palindromic words in bacterial genomes have been shown to be closely correlated to restriction enzyme recognition sites (3,4). On the other hand, careful analysis of over-represented words has been helpful in the detection of transcription factor binding sites (5,6) and in the analysis of polyadenylation signals (7,8) in yeast ORF flanking regions.

Efficient methods in estimating the statistic of a pattern in random texts have been developed during the past years, from Gaussian or Poisson approximations (9–11), generating functions (12–14), to simple recurrence formulae (15). Recently large deviation approaches (16) allowed good estimations of extreme statistics. Today, except for a web site for the analysis of ORF upstream regions (17), there is no general and reliable tool to help a biologist in ranking oligonucleotides of interest. Here we present a simple application which allows the Markovian analysis of a set of words with a chosen fixed length. Two methods are carried out to achieve this goal: exact computation based on recurrence formulae and large deviation approximations. To achieve a good trade-off between speed and precision, we developed an expert system which selects the best method for each word. After a brief mathematical introduction and a presentation of the web interface, we will detail the way the software chooses between the two methods.

MATERIAL AND METHODS

Mathematical background

Markov models and probabilities of words

We consider a sequence X over a finite size alphabet

(for example

for DNA sequences) assumed to be generated from an order m Markov model.

For a given word W of length h, we denote as N(W) its number of (possibly overlapping) occurrences in the sequence X. A pattern

is defined as the finite family of words {W₁,…,W_r}. Its number of occurrences is simply calculated as:

We now consider an observed sequence x (for example, a DNA sequence) and we say that a pattern

is over- (respectively under-) represented if:

where n_W is the number of occurrences of

in the observed sequence and E[N_W] is the mathematical expectation of N_W.

z-score

For a pattern

we define its z-score Z_W according to:

if

is over-represented (i.e. is observed more than expected). Otherwise, according to:

if

is under-represented.

In both cases,

denotes a Gaussian distribution, and P is the probability symbol. Using this convention, Z_W will be positive (respectively negative) for over- (respectively under-) represented patterns. The use of this statistic enables the representation of the p-value in a Gaussian scale, albeit this choice does not mean we use a Gaussian approximation for the computation of that p-value. For example, we can say that a pattern with Z_W larger than 2.96 (the Gaussian quantile for a probability of 0.05), is significantly over-represented at a 5% level.

Robin and Daudin (15) have proposed a method based on generative series and simple recurrences to compute the exact value of Z_W. Nuel (16) also proposed the use of a large deviation approach to get an asymptotic approximation of the same z-score. In the following, we will denote by Z_W^SR the z-scores computed with the simple recurrence method and by Z_W^LD those obtained with the large deviation.

Web interface

We have developed a web interface called SPA (Statistics for PAtterns) whose purpose is to provide a simple access to the patterns z-score computed through these two methods [simple recurrence (SR) and large deviation (LD)].

A SPA request consists of: (i) a set of sequences (in FASTA format); (ii) a list of patterns or a fixed word length when all words are selected; and (iii) the order of the Markov model. The parameter of this model is estimated on the set of sequences using the maximum likelihood. Pattern counts are also obtained on this set of sequences. Explicit selection of the method is possible, but nevertheless it is recommended to leave this parameter on auto since it selects the most suitable computation for each word.

The size n of the chosen sequence (or the size of the longest sequence) is directly related to the efficiency of the different methods. As the LD method proposes an asymptotic approximation, its results will obviously be more reliable as n grows. On the other side, time complexity of the SR approach is in O(n²), so it is quite clear that high values for n are not recommended here. In practice, SR method will be limited to sequences smaller than 100 kb (n=10⁵).

Each pattern must be described with a braced string using the following conventions:. means any letter and [ ] can be used to describe several possible letters for a single position. Union of patterns can be done by concatenation of their string definitions. Table 1 illustrates some examples of syntax and the resulting patterns. The length h of a pattern will be defined as the length of the longest word in it. The size r of a pattern will be the number of words it contains. For the LD method, h will be a critical parameter as memory and time complexity are in O(k^h) where k is the size of the alphabet (usually four for DNA sequences). In practice, LD will be limited to patterns of size smaller than 10. For the SR method, there is no such limitations concerning h, but as time complexity grows with r², very large patterns are generally to be avoided.

Table 1. Complete description of patterns for different string definitions.

As said in the introduction, a Markov model of order m preserves the counts of length m+1 words. Therefore, m will be limited to h−2, due to the fact that the estimation is done on sequences. Obviously, the quality of the estimation depends on the total length l of the provided sequences. Practically, l should be a O(4^m) kb to give the user a satisfying estimate. Furthermore, memory and computational complexity inherent to Markov models limit the maximal order to four with SR, and six and LD.

RESULTS AND DISCUSSION

Interpreting results

Here, we will present two short examples, the first one showing an academic test on biologically known patterns and the second one detailing a sample output.

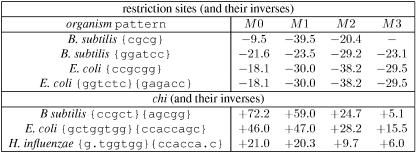
Table 2 shows Z_W^LD statistics for patterns known to be restriction enzyme recognition sites and chi patterns in three bacterial genomes. The statistic is given for orders from 0 to 3. As expected, all of these patterns have very high significance; restriction sites are largely under-represented (p-value close to 10⁻³⁴¹ for example with a z-score of −39.5) and chi patterns are largely over-represented (p-value around 10⁻¹¹³⁴ with a z-score of +72.2). We can also see that this z-score has a great dependence with the order of the chosen model (which is not a surprise). Therefore, it is quite clear that a user who wants to rank a set of patterns should be aware of this and perform at least two different computations for two different orders.

Table 2. z-scores computed through the large deviation for restriction sites and chi patterns with various Markov model orders.

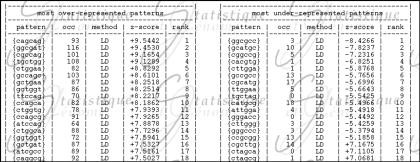
In Figure 1, we can see a sample of ranked output. For more convenience, two tables, listing respectively the most over- and under-represented words are joined in the output. For each pattern is indicated its number of occurrences, the method used (LD or SR), the computed z-score and the rank. As we observe here highly significant patterns, the large deviation provide the best results and that is why there is no use of SR methods in that output. Many patterns among the over-represented ones are closely related to gctggtgg the chi of Escherichia coli (gctggt, ctggtg, ggtggt) or to its inverse ccaccagc (ccagca, ccagcg). For under-represented patterns, we can see the restriction site ccgccg well ranked (rank 15) as well as many palindromes (ggcgcc, gcatgc, …). Finally, we can observe that there is a great difference between that statistical ranking and the frequencies ranking. This can show the value of performing this kind of statistical analysis rather than simple frequency comparison.

Figure 1.

Sample output from SPA for the following request: all words of length h=6 in the first 100 kb of the complete genome of E.coli with a Markov model of order 1.

Methods comparison

Here we want to take into account the limitations highlighted in the section on web interface, as well as the accuracy of the different approaches, in order to help the users to make a choice between the two methods.

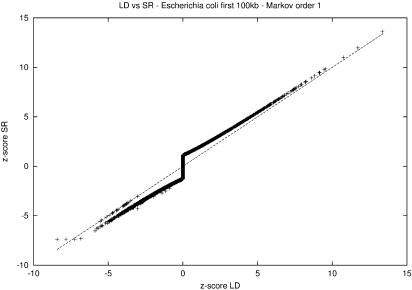
As we need to compute our results with both the methods, we have chosen to work with a not too long sequence consisting of the first 100 kb of E.coli. All the 4096 words of length six are studied and the results are plotted in Figure 2.

Figure 2.

Comparison of the z-scores obtained through large deviation (LD) and simple recurrence (SR) methods for all words of length h=6 on the first 100 kb of E.coli genome for Markov model of order m=1.

Overall, the two methods appear to give similar results. As expected, the large deviation fail to give correct answers for words with a high p-value (above 1% which means |z-score|≤2.3). We also know that the LD z-score gets more accurate as the |z-score| grows and that is exactly what we observe. When the z-score >5, SR and LD do equally well, and the ranking is preserved; it is a reliable region for LD. For negative z-scores, very small probability sums induce computational errors with the SR method; this explains the four words present on the extreme left of Figure 2. As we prefer ranking preservation rather than exact results, we decided to cut the reliable region for SR at −2.5.

For a given pattern on a sequence whose length n is in SR requirement (n≤100 kb, we propose to do the following: first we perform an evaluation using LD and if the z-score is in the range [−2.5; +5] another computation using SR is then performed.

CONCLUSION

The value of using statistical significance rather than frequencies to rank patterns has been shown many times. The usual problem is that there are many different methods and programs to compute those statistics. With our user friendly web interface, we provide a simple way to access two of these methods (large deviation approximations and exact computations using simple recurrence) and we also facilitate the choice with an empirical decision rule.

In the near future, we plan to integrate more methods in SPA (Gaussian and compound Poisson approximations, generative series) to improve both speed and accuracy of the tool. We also plan to use exact computation of the expectation value and the variance of N_W provided by RMES (10) to make an easier choice between the different methods.