Figure 2.

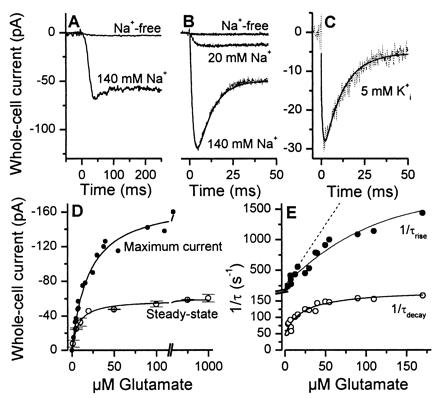
(A) Typical whole-cell current recording from an HEK_EAAC1 cell. Glutamate (100 μM) was applied to the cell by rapid solution exchange in the absence (upper trace) and presence (lower trace) of 140 mM extracellular Na⁺ [V = 0 mV, KSCN-based intracellular solution, Na⁺ replaced by N-methyl-d-glucamine (NMG⁺)]. In this, and the following figures showing experiments in the absence of dl-threo-β-benzyloxyaspartate (TBOA) the leak current was subtracted. (B) Laser-pulse experiment with the same cell as in A at extracellular Na⁺ concentrations of 0, 20, and 140 mM. Glutamate was released from 500 μM α-carboxy-o-nitrobenzyl-caged glutamate with a 340-nm laser flash (180 mJ/cm²) at time 0. The solid line represents the best fit to the data according to the equation I(t) = −I_∞ + I_maxexp(−t/τ_rise) − (I_max − I_∞)exp(−t/τ_decay). I represents current at times t (I(t)), t = ∞ (I_∞), and at the maximum of the response (I_max). The time constants for the rise and the decay of the current were τ_rise = 1.9 ± 0.1 ms and τ_decay = 8.0 ± 0.1 ms, respectively. The concentration of photolytically released glutamate was 45 ± 10 μM. (C) Similar laser-pulse experiment, but in the presence of only 5 mM intracellular K⁺ (K⁺ was replaced by NMG⁺, the intracellular anion was NO₃⁻). The time constant τ_decay was 9.8 ± 0.6 ms (fit shown as solid line). (D) The steady-state (○, rapid solution exchange) and maximum (●, laser-pulse photolysis) current is shown as a function of glutamate concentration (V = 0 mV, n = 4, error bars indicate ± SD). The line represents the best fit according to I = I_max(L/(L + K_app))ⁿ (see text). (E) Glutamate concentration dependence of 1/τ_decay (○) and 1/τ_rise (●) (V = 0 mV, four different cells). The lines represent the best fits according to Eqs. 2A and 2B (k_op = 1400 s⁻¹ and k_cl = 630 s⁻¹; see Results for the other parameters). The broken line represents a simulation of a simple bimolecular glutamate:transporter binding reaction with a slope of k_d = 2⋅10⁷ M⁻¹⋅s⁻¹ and k_−d = 250 s⁻¹.