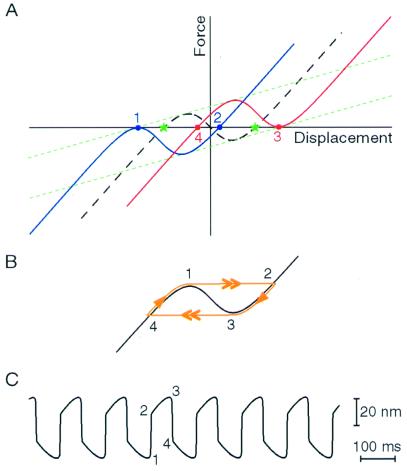
Figure 3.
A model of the hair bundle's spontaneous oscillation. (A) The channel open probability equilibrates with the tension in the gating springs on a time scale much faster than that of adaptation. Under this quasistatic condition, a free bundle must reside at a point of zero force. The region of negative slope stiffness in the initial displacement-force relation (dashed black curve) implies that the bundle is bistable: there are two such points (green stars). Assuming that the bundle first occupies the negative stable point, the transduction channels' low open probability causes adaptation to shift the displacement-force relation in the negative direction. The shift proceeds with a slope set by the stiffness of the stereociliary pivots (ref. 15; dotted green lines). When the relation's left-sided local maximum becomes tangent to the abscissa (at point 1 on the blue curve), however, the negative stable point vanishes, and the bundle must leap to the positive stable point (point 2) to maintain the zero-force condition. For the parameter values of Fig. 1C, this transition corresponds to an abrupt increase in the channel's open probability from 0.15 to 1.0. At the bundle's new position, the channels' high open probability promotes adaptation in the opposite direction until the bundle's position corresponds to the right-sided local minimum of the displacement-force relation (point 3 on the red curve) and the bundle jumps in the negative direction (to point 4). The channel's open probability correspondingly plummets from 0.85 to 0.0. Oscillation ensues from repetition of this sequence. (B) Trajectory (1 → 2 → 3 → 4) of the hair bundle along the displacement-force relation as this relation undergoes the adaptive shift depicted in A. The double arrows indicate the fast transitions across the unstable region of negative stiffness (1 → 2 and 3 → 4), whereas the single arrows demarcate the slow adaptive movements along the stable branches of the relation (2 → 3 and 4 → 1). C, Hair-bundle oscillation produced by a model of bundle mechanics that incorporates the parameter values for the cell whose response is depicted in Fig. 1A. The numbers relate phases of the oscillation to points on the displacement-force relations of A and B.