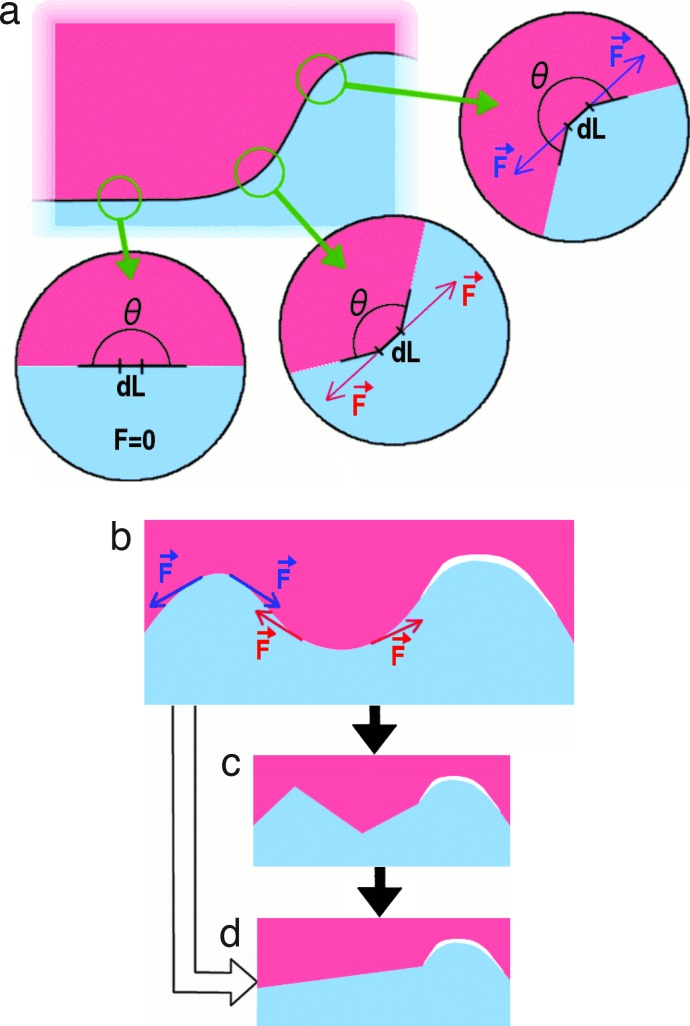
Fig. 2.

Forces in a continuous version of the Schelling model. The evolution of clusters can be analyzed by considering the forces on the surface of a cluster, where the utility function defines the surface tension force (Eq. 1). (a) Shown are forces on infinitesimally small sections dL of the surface when x = 0.5 in the utility function from Eq. 2. Vector colors correspond to the color of the cluster experiencing these forces. (b–d) A sequence in surface evolution. The forces have a tendency to flatten the surface (b → d), but this process will go through an intermediate phase (solid arrows), where the surface flattens first locally (b → c → d), if agents are allowed to move only to the closest available location. The evolution is faster (hollow arrow) if agents can move any distance because then they can immediately participate in flattening of the whole cluster. Empty space (white regions) can form a boundary layer where the surface can maintain its irregular shape.