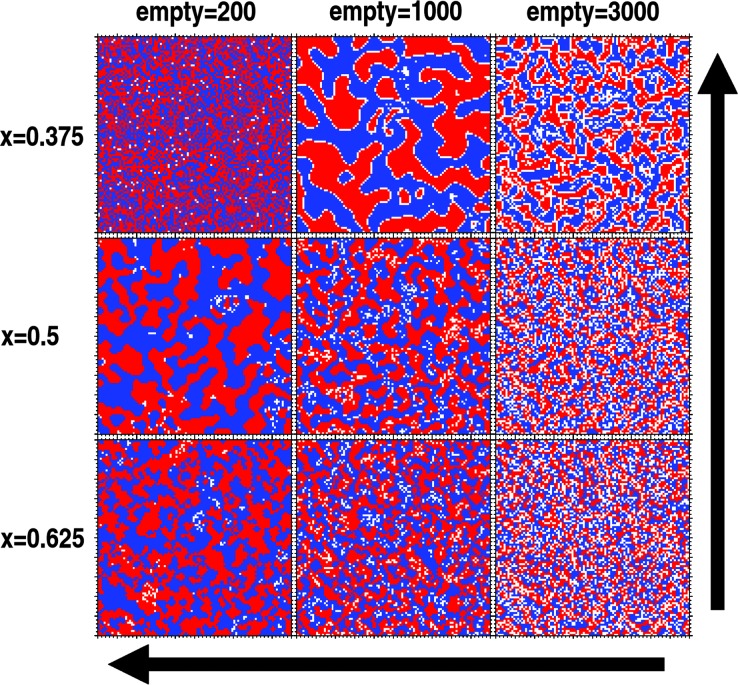
Fig. 3.

The Schelling model forming a solid structure. This figure is a mosaic of results based on the Schelling model when agents are allowed to move only if their utility strictly increases (that is, energy decreases). This restriction brings the whole system to a halt after all agents reach their maximum utility. In the context of the physical analogue, we can say that the system is frozen into a solid. The utility is given in Eq. 2, and results are shown for three values of x: 0.375 = 3/8, 0.5 = 1/2, and 0.625 = 6/8. The grid size is 100 × 100 and the number of blue and red agents is the same. The number of empty cells is indicated. Arrows show directions of increased clustering. Because a smaller x means a stronger preference for neighbors of the same kind, clustering increases as the value of x decreases. On the other hand, empty space provides boundary layers that can stabilize clusters. Hence, less empty space means larger clusters because of their smaller surface-to-volume ratio. Notice, however, that the model with small x and a small number of empty spaces (x = 0.375, 200 empty cells) does not follow these trends and remains poorly clustered. This exception occurs because many agents are stranded with low utility, but without any empty space to which they could move and increase their utility. Periodic boundaries and distance of movement allowed do not influence the clustering behavior of these models.