Abstract
Aim: To determine any differences between the predictive abilities of the IOL calculation formulas of SRK-II and SRK-T and to compare these using two different IOL types.
Methods: A prospective, consecutive, single surgeon clinical trial was conducted on 400 consecutive patients who received routine, standardised phacoemulsification cataract surgery. 200 had cataract surgery and had the Alcon MZ30BD, a 5.5 mm one piece PMMA IOL, and another 200 cases used the Chiron C11UB, a silicone plate haptic IOL. The data used optimised A-constants. The measures were preoperative axial length and keratometry, IOL implanted, and refractive error at 4–6 weeks postoperatively.
Results: There was no significant difference between the predictive abilities of SRK-II or SRK-T. For the Alcon and Chiron lens respectively, prediction errors using SRK-II were <0.5 dioptres in 58% and 70% and for <1.0 dioptres in 84% and 92%. These differences were statistically significant (χ2, p=0.02).
Conclusion: There are differences in the predictability of refractive outcomes between intraocular lens styles.
Keywords: refractive outcome, cataract surgery
Implant power calculation formulas attempt to provide a predictable refractive outcome based on preoperative assessments.1–5 With modern phacoemulsification the preoperative and postoperative axial length and keratometry are broadly unchanged. Therefore, the ultimate determinate of the refractive outcome is the actual anterior chamber depth (ACD) of the implanted intraocular lens (IOL). Because the crystalline lens is approximately 5 mm thick and an IOL is about 1 mm thick, an implant placed within the capsular bag is subject to a variety of potential influences on the final lens location and hence ACD.
The hypothesis of this paper was that there might be design factors in the IOL that may have a significant influence on ACD. Therefore, this study examined two IOL styles that maximally exaggerated lens design while being suitable for phacoemulsification. The Alcon IOL used was a common non-foldable PMMA lens of conventional design whereas the Chiron lens was a plate haptic design.
The paper also hypothesised that with data from a single surgeon using a single set of equipment, there may be differences in using the implant calculation formula SRK-II and SRK-T. The ACD constant for SRK-T may be supplied by the manufacturer or may be calculated4,5 from the SRK-II A-constant by using the formula:
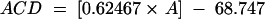 |
METHODS
A prospective cataract database provided data from consecutive patients undergoing cataract surgery by a single, experienced phacoemulsification surgeon (ME). The study compared 200 cases with the Alcon MZ30BD, a 5.5 mm one piece PMMA lens with 5 degree haptic angulation, and 200 cases with the Chiron C11UB, a one piece plate haptic silicone lens. The Alcon IOL was used in the first 200 cases and the Chiron IOL in the next 200 consecutive cases. The surgeon does approximately 500 phacoemulsification cases per year and neither his technique nor abilities changed over the study period. Preoperative keratometry and applanation sonography axial length measurements were all performed by a single technician using the same equipment (Teknar Ophthasonic a-scan III, Teknar, St Louis, MO, USA). The surgery consisted of routine phacoemulsification cataract extraction. The wound was a linear scleral incision, 2 mm behind the limbus at the 12 o'clock position. The PMMA lens had a 5.7 mm wide incision sutured with one 10/0 nylon suture whereas the plate haptic lens had an unsutured 3.2 mm incision. Otherwise, the surgery was identical for both lens types. The capsulorrhexis was approximately 5 mm in diameter. The inclusion criteria were all consecutive cases of phacoemulsification. The exclusion criteria were combined procedures, capsule rupture, and failure to place the lens in the bag. The author determined the spectacle refraction at 4–6 weeks postoperatively.
Calculations were based on the preoperative keratometry and axial length, the IOL power used, and the postoperative refraction, which was reduced to a spherical equivalent. For each case, the standard formulas for SRK-II and SRK-T were used to calculate the individual A-constants for that patient.4,5 These were aggregated to determine the actual A-constant for the lens type and for each formula. Hence the A-constant gives a mean absolute error of zero for each of these datasets. This new A-constant was used for each patient to predict the refractive outcome, given the actual IOL used. The difference between the predicted outcome and actual outcome is the variance in spherical equivalence. These calculations were performed using SRK-II and SRK-T for both lens types. The standard error of equivalence was calculated5 and data were compared using χ2 tests with Yates's correction where appropriate. Data analysis only occurred after all 400 cases were complete.
RESULTS
The keratometry, axial length, and IOL powers used are detailed in Table 1. There was no statistically significant difference between the keratometry and axial length of those patients receiving the Alcon or Chiron IOL. The A-constants supplied by the IOL manufacturer and the calculated A-constants are given in Table 2. The standard error of estimate is detailed in Table 3 and the variance of outcome of spherical error is detailed in Table 4. This is the difference between the calculated and actual outcomes using the optimised A-constant. There were statistically significant differences for the following; for variances of <0.5D and <1.0D the Chiron IOL performed better than the Alcon using SRK-II (70% v 58%, p=0.02, 92% v 84%, p=0.02 respectively); the Chiron achieved more cases <0.5D than the Alcon using SRK-T (68% v 56%, p=0.02, there was no difference in outcomes for total cases <1.0D and <2.0D); there was no significant difference in using SRK-II and SRK-T for the Chiron lens (70% v 68% <0.5D, 92% v 90% <1.0D); there was no significant difference between SRK-II and SRK-T for the Alcon lens although for errors <1.0D p=0.049.
Table 1.
Keratometry, axial length, and IOL implanted
| Alcon (n=200) | Chiron (n=200) | ||
| Keratometry | (mean) | 43.29 (1.57) | 43.77 (1.51) |
| (D) (SD) | (range) | 40.25–47.87 | 41.25–47.0 |
| Axial lengths | (mean) | 23.39 (1.13) | 23.16 (1.03) |
| (mm) (SD) | (range) | 21.30–26.39 | 21.15–25.75 |
| IOL power | (range) | 12.0–27.0 | 13.0–26.0 |
Table 2.
Actual and calculated A-constants
| Alcon MZ30BD | Chiron C11UB | |
| Recommended (SRK-II only) | 118.7 | 119.0 |
| SRK-II (calculated) | 118.7 | 119.0 |
| SRK-T ACD (calculated) | 5.183 | 5.401 |
| SRK-T A-constant (calculated) | 118.35 | 118.7 |
Table 3.
Standard error of estimate
| Alcon | Chiron | |
| SRK-II | 0.6768 | 0.6473 |
| SRK-T | 0.6405 | 0.6469 |
Table 4.
Variance of outcome of spherical equivalence
| SRK-II | SRK-T | |||
| Alcon | Chiron | Alcon | Chiron | |
| <0.5D | 58% | 70% | 56% | 68% |
| <1.0D | 84% | 92% | 91% | 90% |
| <2.0D | 99% | 98% | 99% | 98% |
DISCUSSION
Implant power calculation formulas typically derive from either an empirical or theoretical background—for example, SRK-II and SRK-T respectively.5 However, all formulas use some sort of “constant” that can be optimised for an individual surgeon and IOL type. This optimisation is achieved by taking preoperative parameters and postoperative outcomes of a given database of patients and back calculating the constant. The origin and composition of these datasets are vital to understand the applicability of a given power calculation formula.2 Some sets are composites of several surgeons, some of several IOL styles.5
Retzlaff et al4 used an unselected data set of 1677 cases to compare the formulas of SRK-T, Holladay, SRK-II, Hoffer and Binkhorst II. For errors <0.5D the percentages achieved were 50%, 50%, 48%, 42%, and 47% respectively for which Hoffer was significantly worse (p=0.0001) but the other formulas were statistically similar. For errors <1.0D the outcomes were 80%, 80%, 77%, 78%, and 78% for which SRK-II was significantly worse than SRK-T and Holladay (p=0.03) but no other differences were significant. For errors >2.0D, SRK-T, SRK-II, and Holladay were significantly better than Hoffer and Binkhorst (p=0.02).
Sanders et al5 used a data set of 990 unselected cases from multiple surgeons and seven IOL styles to compare SRK-T, Holladay, SRK-II, Hoffer and Binkhorst II formulas. The outcomes were that the percentages that achieved a spherical error of <0.5D were 30%, 30%, 29%, 28%, and 29% respectively and an error of <1.0D was achieved in 81%, 81%, 79%, 77%, and 77% respectively. For unselected cases it would appear that SRK-T and the Holladay formulas are best. However, analysing Sanders et al's data (1990) with χ2 and Yates's correction there was no significant differences between any formulas for errors <0.5D and the only significant difference for errors <1.0D are that SRK-T and Holladay was better than Hoffer and Binkhorst (81% v 77%, p=0.03). SRK-II was not significantly different from SRK-T or the Holladay formula.
Sanders et al5 selective data for eyes with an axial length less than 22.0 mm (n=99) showed no difference between any of the five formulas at errors <0.5D, <1.0D or >2.0D (χ2 with Yates's correction).
The situation is different for longer eyes. Using Sanders et al's dataset5 for all eyes with axial lengths >27.0 mm (n=40), the results for SRK-T, Holladay, SRK-II, Hoffer and Binkhorst II formulas for errors less than 0.5D are 45%, 45%, 25%, 45%, and 40% respectively for which there are no significant differences between the formulas. For errors <1.0D the results are 85%, 70%, 40%, 63%, and 70% respectively for which there is no difference between SRK-T, Holladay and Binkhorst but all of these are significantly better than SRK-II (p=0.01). For errors greater than 2.0D the results are 2.5%, 2.5%, 20%, 2.5%, and 2.5% for which SRK-II is significantly worse (p=0.03). Hence, SRK-II is worse overall for these long eyes whereas there is little difference between the other formulas.
Hoffer1 published a series of 450 cases that were single surgeon, single technician, single IOL style. For SRK-II, SRK-T, Holladay and Hoffer-Q an error of SD 0.5D was present in 57%, 62%, 65%, and 66% respectively and for errors (SD 1.0D) the results were 88%, 92%, 93%, and 93%. The mean preoperative axial length was 23.56 (SD 1.24) mm and the keratometry was 43.83 (SD 1.56) D. This is very similar to this series as are the outcomes. Hoffer found that SRK-T, Holladay and Hoffer were statistically similar and all were better than SRK-II with axial lengths greater than 26.0 mm.
Sanders et al5 study showed that for SRK-II, 30% achieved an error of <0.5D and 81% <1.0D. This compares with this current study of the Alcon IOL of 58% and 84% respectively and the Chiron IOL as 70% and 92%. One explanation for the differences is that there is less variation in outcome with a single surgeon and a single technician performing the preoperative measurements using the same equipment. Hoffer's series1 supports this contention. Within this context, there was essentially no difference in the predictability of outcome with SRK-II and SRK-T although it is recognised that no eye had an axial length greater than 26.39 mm
There is a huge difference between predictability and surgeons. Retzlaff et al4 used five datasets each from a different surgeon and for SRK/T the standard error of estimate ranged from 0.63–1.02 between the five. The mean was 0.86 and similarly the mean for the same surgeons for SRK/II was 0.89 and for Holladay was 0.88. It appears that there is more variability between surgeons than there is between formulas; however, none of the five sets allowed comparison of a single surgeon and two lens types or vice versa. Similarly, Holladay et al3 used 12 surgeons' data and showed a range of mean absolute error from 0.48 to 0.81 for his formula. The lens styles were not quoted.
This study chose two entirely different styles of IOLs to determine if there was a difference in refractive predictability between lenses. If it is assumed that an eye retains similar axial lengths and keratometry before and after surgery, and if IOL powers are accurately stated by the manufacturer then the only explanation for a more consistent refractive outcome is that the ACD is more predictable. It is conceivable that a plate haptic IOL may locate in a more reproducible place than a 5.5 mm PMMA IOL with conventional haptics but the author can find no evidence to support or refute this suggestion.
The manufacturers recommended A-constants were very accurate (Table 2). However the calculated SRK-T A-constant equivalent differed by 0.3 from the actual SRK-II A-constant for both IOL types. If the conversion formula is altered to ACD = [0.623 × A-constant] − 68.747 then the manufacturers' supplied A-constant for the Alcon and Chiron IOLs ACD-constant is automatically corrected to less than 0.08D of actual.
Rapid responses.
Letters on the following British Journal of Ophthalmology papers have been published recently as rapid responses on the BJO website. To read these letters visit our website www.bjophthalmol.com and click on “Read eLetters”
R J C Bowman, H Faal, M Myatt, et al. Longitudinal study of trachomatous trichiasis in the Gambia. Br J Ophthalmol 2002;86:339–43.
J Plšková, L Kuffová, V Holáň, et al. Evaluation of corneal graft rejection in a mouse model. Br J Ophthalmol 2002;86:108–13.
L Xie, X Dong, W Shi. Treatment of fungal keratitis by penetrating keratoplasty. Br J Ophthalmol 2001;85:1070–4. If you would like to post an electronic response to these or any other articles published in the journal, please go to the website, access the article in which you are interested, and click on “eLetters: Submit a response to this article” in the box in the top right hand corner.
REFERENCES
- 1.Hoffer KJ. The Hoffer Q formula: a comparison of theoretical and regression formulas. J Cataract Refract Surg 1993;19:700–12. [DOI] [PubMed] [Google Scholar]
- 2.Holladay JT, Prager TC, Ruiz RS, et al. Improving the predicability of intraocular lens power calculations. Arch Ophthalmol 1986;104: 539–41. [DOI] [PubMed] [Google Scholar]
- 3.Holladay JT, Praeger TC, Chandler TY, et al. A three-part system for intraocular lens power calculations. J Cataract Refract Surg 1988;14:17–24. [DOI] [PubMed] [Google Scholar]
- 4.Retzlaff JA, Sanders DR, Kraff MC. Development of the SRK/T intraocular lens implant power calculation formula. J Cataract Refract Surg 1990:333–40. [DOI] [PubMed]
- 5.Sanders DR, Retzlaff JA, Kraff MC, et al. Comparison of the SRK/T formula and other regression formulas. J Cataract Refract Surg 1990;16:341–6. [DOI] [PubMed] [Google Scholar]


