Abstract
The experimental determination of protein compressibility reflects both the protein intrinsic compressibility and the difference between the compressibility of water in the protein hydration shell and bulk water. We use molecular dynamics simulations to explore the dependence of the isothermal compressibility of the hydration shell surrounding globular proteins on differential contributions from charged, polar, and apolar protein-water interfaces. The compressibility of water in the protein hydration shell is accounted for by a linear combination of contributions from charged, polar, and apolar solvent-accessible surfaces. The results provide a formula for the deconvolution of experimental data into intrinsic and hydration contributions when a protein of known structure is investigated. The physical basis for the model is the variation in water density shown by the surface-specific radial distribution functions of water molecules around globular proteins. The compressibility of water hydrating charged atoms is lower than bulk water compressibility, the compressibility of water hydrating apolar atoms is somewhat larger than bulk water compressibility, and the compressibility of water around polar atoms is about the same as the compressibility of bulk water. We also assess whether hydration water compressibility determined from small compound data can be used to estimate the compressibility of hydration water surrounding proteins. The results, based on an analysis from four dipeptide solutions, indicate that small compound data cannot be used directly to estimate the compressibility of hydration water surrounding proteins.
INTRODUCTION
The change in physical properties of water in the vicinity of biological molecules is of interest to both experimentalists and computational biologists ((1) and references therein). Protein compressibility obtained from sound velocity measurements is a combination of protein intrinsic compressibility and the change in the compressibility of water in the protein hydration shell. Separating the two contributions is valuable for characterizing both the internal dynamics and flexibility of protein molecules (2,3), as well as the physical properties of water at the protein surface. Protein compressibility measurements provide unique information on the general thermodynamic properties of proteins (4–7), including insights into the behavior of the protein interior (8), conformational transitions (9,10), and molecular interactions (11,12).
In this article, we devise a method to estimate the compressibility of hydration water as a function of the varied chemical nature of the protein-water interface. A description of hydration based on the protein surface composition is attractive because it reflects the chemical nature of the protein-water interface (13). The average solvent-exposed atomic-type composition estimated for a set of 16 globular proteins includes not only charged (12.2%) and polar (37.4%) atoms, but also a substantial number of apolar atoms (50.4%) (14). One argument in favor of an approach based on surface composition is the fact that when only a limited number of water molecules is available, the molecules do not distribute uniformly on the protein solvent-accessible surface. Molecular dynamics simulations have found that 350 water molecules that fully hydrate myoglobin, originally distributed uniformly on the protein surface, arrange in such a way that they hydrate every charged group and cover 83% of the charged surface, 65% of the hydrophilic surface, and only 53% of the hydrophobic surface (15).
Protein-water interactions are fundamental to the description of protein physical properties (1,16,17). The hydration properties of water play an important role in the formation of the three-dimensional native structures of proteins and nucleic acids, and the dynamics of biological molecules (18). Proteins do not perform their functions until a critical hydration level is achieved, and in some cases, the level of hydration that is required to restore enzymatic activity is less than one layer of water molecules (19). A detailed description of the structure and properties of water in the protein hydration shell is essential for our understanding of the processes taking place in the interior of a biological cell, a gel-like matrix (20,21) where most water molecules are within a few solvation layers of proteins and other macromolecules.
There has been extensive work through both experimental (22–26) and computer simulations methods (27–32) to explain how solutes, and proteins in particular, change the properties of water layers adjacent to their surface. Theories of hydrophobic hydration (33–36) relate the structural ordering of water by the nonpolar solutes to the hydration thermodynamics through solute-water pair correlations. The special properties of water molecules in the hydration shell of proteins are reflected in the compressibility and density, when compared to bulk water. Others have estimated the compressibility of hydration water (5,37–42) to be, on average, 22% lower than bulk water compressibility. Data from small-angle x-ray scattering combined with neutron scattering studies of lysozyme, thioredoxin reductase, and protein R1 (24) show that the average density of the water in the protein first hydration shell is 10% higher than the density of bulk water, a result that is consistent with experimental findings from x-ray crystallography (43). The estimated values for the hydration water compressibility and density are consistent with each other in that higher density restricts density fluctuations and therefore lowers compressibility.
We report here a model for hydration water compressibility derived from analysis of molecular dynamics (MD) simulations of protein solutions. The approach for estimating protein compressibility from volume fluctuations was established previously based on MD simulations for four globular proteins: trypsin, ribonuclease A, hen egg white (HEW) lysozyme, and α-lactalbumin (44). In our model, the residual compressibility of the water in the protein hydration shell is accounted for by a linear combination of contributions from charged, polar, and apolar solvent-accessible surfaces. The physical basis for the hydration water compressibility model is the variation in water density indicated by surface-specific radial distribution functions (RDFs) of water around charged, polar, and apolar protein surfaces. The outcome is a formula to interpret experimental data on protein solution compressibility by deconvolution of intrinsic protein and hydration contribution when a protein of known structure is investigated. Further, we compare the hydration water compressibility for solvation of proteins with that of small peptides to assess whether hydration water compressibility determined from small compound data can be used to estimate the compressibility of hydration water surrounding proteins. The results indicate that small compound data cannot be directly used to estimate the compressibility of hydration water surrounding proteins.
METHODS
Theoretical methods
The isothermal compressibility of a protein solution, 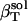 , is defined as the relative change in the solution volume, Vsol, under pressure (P) at constant temperature (T):
, is defined as the relative change in the solution volume, Vsol, under pressure (P) at constant temperature (T):
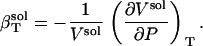 |
(1) |
The total volume is a sum of contributions from the protein molecular volume, Vp, the volume of the bulk water, Vw, and the volume of hydration water, Vh, as follows:
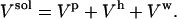 |
Equation 1 can be rewritten as a sum over component volume contributions,
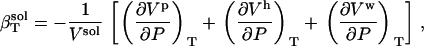 |
(2) |
and again as
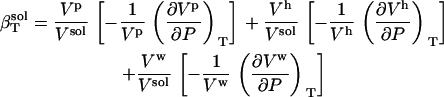 |
(3) |
The ratios between the solution volume components and the total solution volume are the volume fractions: 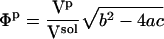 ,
, 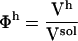 , and
, and 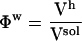 . In Eq. 3, we identify the protein compressibility,
. In Eq. 3, we identify the protein compressibility,
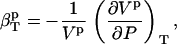 |
hydration water compressibility,
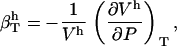 |
and bulk water compressibility,
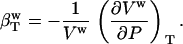 |
Finally, Eq. 2 for the compressibility of the protein solution becomes
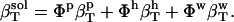 |
(4) |
The hydration contribution to solution compressibility is estimated assuming that all water in the protein solution has the properties of bulk water, and then compare this estimate with the actual 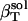 (Eq. 4). In this procedure,
(Eq. 4). In this procedure, 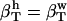 and the ideal solution compressibility is
and the ideal solution compressibility is
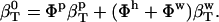 |
(5) |
Any difference between the actual (Eq. 4) and the ideal (Eq. 5) solution compressibility,
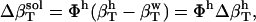 |
(6) |
is due to the fact that hydration water has different compressibility than bulk water. The value 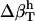 is the difference between the compressibility of hydration and bulk water, respectively.
is the difference between the compressibility of hydration and bulk water, respectively.
For the experimental determination of protein compressibility, the adiabatic compressibility of a solution is given by the Laplace equation, 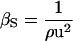 , where ρ is the density of the solution and u is the velocity of sound through the solution. The experimental, apparent partial adiabatic compressibility of a protein, is defined as the limit at 0 protein concentration of the following expression (38):
, where ρ is the density of the solution and u is the velocity of sound through the solution. The experimental, apparent partial adiabatic compressibility of a protein, is defined as the limit at 0 protein concentration of the following expression (38):
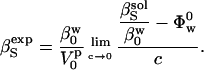 |
(7) |
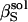 is the adiabatic solution compressibility,
is the adiabatic solution compressibility, 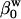 is the compressibility of water,
is the compressibility of water, 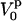 is the partial specific volume of the protein, and
is the partial specific volume of the protein, and 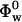 is the apparent volume fraction of the solvent in solution. The apparent protein compressibility has contributions from both intrinsic protein compressibility and a hydration contribution.
is the apparent volume fraction of the solvent in solution. The apparent protein compressibility has contributions from both intrinsic protein compressibility and a hydration contribution.
The adiabatic compressibility is related to isothermal compressibility (5):
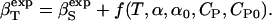 |
(8) |
Here f is a function of the thermal expansion coefficients of water and protein solutions, α and α0, and the heat capacity of water and protein solutions, CP and CP0, respectively.
The following relationship (45,46) may be used to decompose the apparent experimental protein compressibility into an intrinsic protein compressibility, 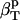 , and a hydration water contribution:
, and a hydration water contribution:
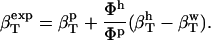 |
(9) |
The hydration contribution reflects the change in the compressibility of the solvent as a result of interactions with the surface-exposed protein atoms. Finally, protein intrinsic compressibility, 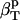 , can be calculated as
, can be calculated as
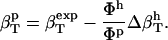 |
(10) |
In this article, we outline a procedure for straightforward determination of the protein intrinsic compressibility, 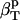 , from the apparent compressibility determined experimentally,
, from the apparent compressibility determined experimentally, 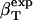 . The central idea of the procedure is the evaluation of
. The central idea of the procedure is the evaluation of 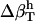 for any protein of known three-dimensional structure.
for any protein of known three-dimensional structure.
Computational methods
Simulations
MD simulations of trypsin, ribonuclease A, lysozyme, and α-lactalbumin were performed for 1 ns in an isothermal-isobaric (NPT) ensemble (constant number of particles, N, constant pressure, P = 1 atm, and constant temperature, T = 300 K), with periodic boundary conditions and the particle-mesh Ewald method (47) for the calculations of the electrostatic interactions. Constant temperature and pressure were maintained using the Nosé-Hoover method of coupling to a heat bath and extended system algorithm for controlling the pressure, with a coupling constant of 25 ps. The computer simulations and post-processing of the generated trajectories are performed with CHARMM (48). More details of the MD simulations for the four globular proteins are described elsewhere (44). MD simulations were also performed for four small dipeptides: alanine dipeptide, glutamic acid dipeptide, aspartic acid dipeptide, and lysine dipeptide. Each −CH3-blocked dipeptide was solvated in a cubic box of 1000 TIP3P water molecules and MD simulations were performed using the same protocol as for proteins (details of the simulations have appeared (49)).
Compressibility calculation
Isothermal compressibility, βT, for proteins, protein and dipeptide solutions, and pure water (TIP3P model), is determined from volume fluctuations, δV2, and average volumes, 〈V〉, according to
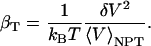 |
(11) |
The protein molecular volume, V(t), is determined using a grid-based, atomic volume expansion algorithm, that allows for the protein interstitial spaces to be included in the total volume together with the protein van der Waals volume (44). Protein volumes are evaluated every ps from a 1-ns equilibrium trajectory with a 0.2 Å grid spacing. The average and standard deviations of the volume distribution are then used to calculate protein intrinsic compressibility,  . The isothermal compressibility evaluated in this manner correlates well with the experimental compressibility. As pointed out in a recent review (7), the suitability of any method for protein volume calculation is validated by the correlation with experiment. The compressibility of the protein and dipeptide solutions is also determined from Eq. 11, using the histogram of the time series of the whole system (simulation box) volume, Vsol(t), rather than molecular volumes.
. The isothermal compressibility evaluated in this manner correlates well with the experimental compressibility. As pointed out in a recent review (7), the suitability of any method for protein volume calculation is validated by the correlation with experiment. The compressibility of the protein and dipeptide solutions is also determined from Eq. 11, using the histogram of the time series of the whole system (simulation box) volume, Vsol(t), rather than molecular volumes.
Errors due to finite grid spacing
We have calculated protein total volume using a grid spacing, δ = 0.2 Å. An upper bound for the errors introduced in the volume calculation by the finite grid spacing can be obtained as follows. Let us assume that our protein is spherical, with a radius of 15 Å. An estimate of the error in volume calculation is given by the ratio of the spherical shell volume at the protein surface with a width of ΔR = δ, 4πR2δ, and the volume of the whole sphere, 4πR3/3. For our particular case, this ratio is 3 × 0.2/15 = 0.04, i.e., 4%. Following the rationale for error calculation described earlier (44), the error in compressibility calculation due to the calculation of volume with a finite grid spacing formula is 4%. This is a maximal error that assumes that all the protein surface is convex, such as the case with a spherical protein. In fact, the protein surface has both convex and concave local geometry (peaks and valleys) and some of the errors (overestimates and underestimates) will cancel out. The total error in the calculation of the total protein volume with a grid spacing of 0.2 Å for a globular protein with a radius of gyration of 15 Å is smaller than 4%.
Atomic categories
To calculate the charged, polar, and apolar contributions to  , surface-exposed protein atoms are placed in three categories: charged (crg); polar (pol); or apolar (apl). Charged atoms include the side-chain carboxyl groups of Asp and Glu, the guanidinium group of Arg, the side-chain amino group of Lys, the amino and carboxylate termini of the polypeptide chain, and the charged Ca2+ ions in α-lactalbumin and trypsin. The polar category includes atoms with an absolute partial charge |qi| > 0.3 e, excluding those atoms defined as charged. All other atoms are apolar atoms. The solvent-accessible surface areas contributed by charged, polar, and apolar atoms (SAStype, type = crg, plr, aplr), as well as the total SAS are calculated with CHARMM with a probe radius of 1.4 Å (based on the algorithm of Lee and Richards (50)).
, surface-exposed protein atoms are placed in three categories: charged (crg); polar (pol); or apolar (apl). Charged atoms include the side-chain carboxyl groups of Asp and Glu, the guanidinium group of Arg, the side-chain amino group of Lys, the amino and carboxylate termini of the polypeptide chain, and the charged Ca2+ ions in α-lactalbumin and trypsin. The polar category includes atoms with an absolute partial charge |qi| > 0.3 e, excluding those atoms defined as charged. All other atoms are apolar atoms. The solvent-accessible surface areas contributed by charged, polar, and apolar atoms (SAStype, type = crg, plr, aplr), as well as the total SAS are calculated with CHARMM with a probe radius of 1.4 Å (based on the algorithm of Lee and Richards (50)).
Radial distribution functions
The radial distribution function (RDF), gAB(R), of atom A, at a distance R from a central atom, B, can be calculated from the normalized histogram of the numbers of atoms, nA(R + 0.5ΔR), in a bin of width ΔR:
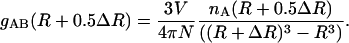 |
(12) |
N is the total number of atoms in the system and V is the volume of the system.
We calculate the 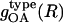 of water oxygen atoms surrounding charged, polar, and apolar groups using CHARMM. The space around each solvent-exposed protein (heavy) atom is divided into concentric spherical shells with a width of 0.1 Å for a total of 100 shells, with R ranging from 0 to 10 Å from the center of each heavy atom on the protein surface. The oxygen-oxygen gOO(R) values in ambient water are calculated from a 20-ns simulation of 2000 water molecules at constant pressure and temperature with periodic boundary conditions and the particle-mesh Ewald (47) summation for the electrostatic interactions. The protein-water RDFs do not converge to 1; instead, they converge to ∼0.62. This is because the volume occupied by the protein is not accessible to the solvent. We renormalized the protein-water RDFs (i.e., multiplied the original curves by 1.61) to converge to 1.0 for easier comparison with gOO(R) of pure water-TIP3 model.
of water oxygen atoms surrounding charged, polar, and apolar groups using CHARMM. The space around each solvent-exposed protein (heavy) atom is divided into concentric spherical shells with a width of 0.1 Å for a total of 100 shells, with R ranging from 0 to 10 Å from the center of each heavy atom on the protein surface. The oxygen-oxygen gOO(R) values in ambient water are calculated from a 20-ns simulation of 2000 water molecules at constant pressure and temperature with periodic boundary conditions and the particle-mesh Ewald (47) summation for the electrostatic interactions. The protein-water RDFs do not converge to 1; instead, they converge to ∼0.62. This is because the volume occupied by the protein is not accessible to the solvent. We renormalized the protein-water RDFs (i.e., multiplied the original curves by 1.61) to converge to 1.0 for easier comparison with gOO(R) of pure water-TIP3 model.
RESULTS
Radial distribution functions of water molecules around charged, polar, and apolar groups in proteins
The radial distribution functions of water oxygen atoms around charged, polar, and apolar protein surfaces were calculated to assess the differences in water structure at different types of protein-water interfaces and to gain insights into the physical basis for hydration water compressibility. A comparison of protein-water RDFs with the bulk water RDFs provides the guidelines for calculating the volume of the protein hydration water, Vh. The distance from the protein surface at which no differences between hydration and bulk water are observed is then used to estimate the hydration water volume and the volume fraction Φh.
Interface-specific RDFs
The interface-specific, cumulative RDF, gc(R), is a sum over all same-type (charged, polar, or apolar) surface-exposed atomic RDFs:
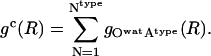 |
(13) |
Atype, type = crg, plr, aplr is a heavy atom on the protein surface (the central atom in Eq. 12) and Owat is the Oxygen atom of water molecules. For this calculation, the exposed surface atoms are those atoms with the time-average 〈SAS〉 larger than 10.0 Å2, to allow full contact with one water molecule.
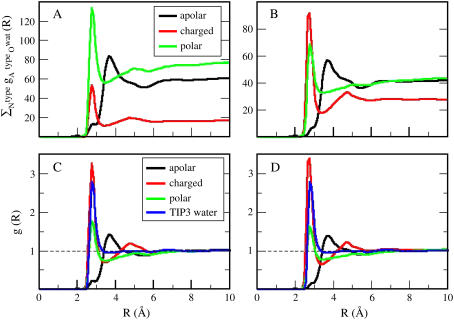
Differences in the cumulative RDFs around charged (red curves), polar (green curves), and apolar (black curves) atoms are shown for trypsin (Fig. 1 A) and α-lactalbumin (Fig. 1 B). The sum of the converged values of the cumulative RDFs is proportional to the total number of heavy atoms that are solvent-exposed in each globular protein. Radial distribution functions, g(R), for the three types of interface are obtained from the normalized cumulative RDFs by scaling with the trajectory-averaged numbers of atoms of each type that are surface-exposed, 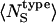 . Three distinct g(R) values, each representing the hydration of a particular type of protein-water interface, are obtained in Fig. 1, C (trypsin) and D (α-lactalbumin).
. Three distinct g(R) values, each representing the hydration of a particular type of protein-water interface, are obtained in Fig. 1, C (trypsin) and D (α-lactalbumin).
FIGURE 1.
Cumulative RDFs for trypsin (A) and α-lactalbumin (B). Charged RDFs are the red curves, polar RDFs are the green curves, and apolar RDFs are the black curves. Normalized RDFs for trypsin (C) and a-lactalbumin (D): charged-groups hydration, red curves; polar hydration, green curves; and apolar hydration, black curves. The oxygen-oxygen RDF for water, TIP3P model, is shown in blue.
The perturbation of water structure by atom types is shown by a comparison of the protein-water g(R) with the oxygen-oxygen gOO(R) for bulk water, the TIP3P model (51) (blue solid curves in Fig. 1, C and D). The width and position of the first peak in the RDFs around charged and polar surfaces (the red and green curves in Fig. 1) are roughly the same as the width and position of the first peak in the gOO(R) in water, whereas their intensities are different: the peak is larger for charged protein groups, indicating that these groups are surrounded by more water molecules than oxygen atoms in bulk water. The peak is less intense for the RDF from the polar atomic groups in proteins indicating that they are less hydrated than charged atoms. In contrast, the position of the main peak in the RDFs of the apolar surface (black curves in Fig. 1) is shifted away from the surface, and the peak is wider and smaller than the first peak in the RDFs of the charged and polar surfaces.
In liquid water under ambient conditions, each water molecule is surrounded on average by 3.8 closest neighbors. At the protein-water interface, approximately half of the configurational space is available to water, which means that each heavy atom should be in the proximity of ∼1.9 water molecules. We calculate the average number of hydration waters in the protein first hydration shell (to a radial distance of 3.2 Å from the protein atoms), and find that there are 2.7 water molecules hydrating charged groups, 1.5 water molecules for polar groups, and 1.1 for apolar groups.
The results presented here provide a physical basis for the decomposition of the protein hydration volume into contributions from charged, polar, and apolar hydration volumes. No discernable differences in the protein-water RDFs and bulk water are detected beyond 8 Å from the protein surface. MD simulations of proteins typically include 2–3 layers of water molecules separating the protein from the wall of the simulation box. As such, the majority of the water in the simulation box can be approximately characterized as hydration water.
Local environment
At the protein-water interface, the individual atomic group-specific RDFs are influenced by two factors of the local environment: the unique configuration of neighboring amino acids, and the local topology of the solvent-accessible surface, which could be convex or concave. Effects of the local environment are manifested in the differences on the RDFs for the same chemical group from individual residues. The RDFs of same-type atomic group vary somewhat in magnitude but the structural distinctions between atomic types apparent in the RDFs in Fig. 1 are consistently manifested for individual residues (results given in Supplementary Material). Difference in positions of the first hydration shell are due partly to local surface topology. That is, the maximum position at smaller distances for charged groups reflects the convex surface where these residues are generally located, while the shift toward larger distances is consistent with a concave surface for apolar groups.
Model: hydration shell compressibility as a function of the chemical nature of the protein-water interface
To assess the change in compressibility due to protein hydration we formulate a simple model where the compressibility of the hydration water,  , has contributions dependent on the nature of the protein surface exposed to water: charged, polar, and apolar. To estimate these contributions, we first identify the hydration contribution to the solution compressibility as the residual compressibility,
, has contributions dependent on the nature of the protein surface exposed to water: charged, polar, and apolar. To estimate these contributions, we first identify the hydration contribution to the solution compressibility as the residual compressibility, 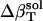 (Eq. 6)—the difference between the actual isothermal compressibility of the protein-water solution (
(Eq. 6)—the difference between the actual isothermal compressibility of the protein-water solution (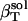 estimated from simulation)—and an ideal protein-water solution compressibility, which does not take into account changes in the solvent compressibility due to protein solvation,
estimated from simulation)—and an ideal protein-water solution compressibility, which does not take into account changes in the solvent compressibility due to protein solvation, 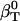 . If water and the protein molecule are assumed to be independent components of the protein-water system,
. If water and the protein molecule are assumed to be independent components of the protein-water system, 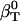 can be estimated from the intrinsic protein compressibility,
can be estimated from the intrinsic protein compressibility, 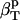 , and the compressibility of the bulk water,
, and the compressibility of the bulk water, 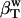 , weighted by their corresponding volume fractions, Φp and Φh + Φw, according to Eq. 5.
, weighted by their corresponding volume fractions, Φp and Φh + Φw, according to Eq. 5.
The actual isothermal compressibility of the protein-water solutions and bulk water systems are calculated from the whole simulation box average volume, 〈Vsol〉, and fluctuations, 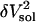 , according to Eq. 11. The calculated protein-water solution compressibility,
, according to Eq. 11. The calculated protein-water solution compressibility, 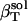 (Table 1), is between 52 and 55 10−6 atm−1. The compressibility of bulk water (TIP3P model) calculated from whole system volume fluctuations is 61 10−6 atm−1 (44,51). Intrinsic, isothermal protein compressibility,
(Table 1), is between 52 and 55 10−6 atm−1. The compressibility of bulk water (TIP3P model) calculated from whole system volume fluctuations is 61 10−6 atm−1 (44,51). Intrinsic, isothermal protein compressibility, 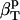 , is calculated from protein volume fluctuations, δV2, and average volumes, 〈V〉, as described previously (44). The values
, is calculated from protein volume fluctuations, δV2, and average volumes, 〈V〉, as described previously (44). The values  and
and 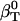 are listed in Table 1.
are listed in Table 1.
TABLE 1.
Solution compressibilities, 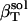 , calculated from simulation box volume fluctuations,
, calculated from simulation box volume fluctuations, 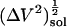 , and average, 〈V〉 sol
, and average, 〈V〉 sol
| Trypsin | RNAse A | HEW Lyso | α-Lacta | |
|---|---|---|---|---|
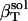 |
55 | 54 | 52 | 53 |
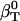 * *
|
52.3 | 53 | 52.8 | 53.6 |
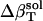 † †
|
2.7 | 1.1 | −0.8 | −0.6 |
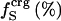 |
9.0 | 14.0 | 16.0 | 18.0 |
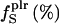 |
40.0 | 35.0 | 38.0 | 29.0 |
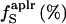 |
51.0 | 51.0 | 46.0 | 53.0 |
| Error ΔβT (%)‡ | 4 | 10 | 1.7 | 4.3 |
Volumes are reported as Å3 and compressibilities as 10−6 atm−1.
Solution compressibility using the calculated protein compressibility,  (44), bulk water compressibility,
(44), bulk water compressibility, 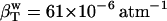 , and volume fractions, Φp and Φw = 1 − Φp.
, and volume fractions, Φp and Φw = 1 − Φp.
 .
.
Errors in the calculation of residual hydration water compressibility from the estimated changes in hydration water compressibility: 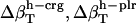 , and
, and 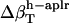 .
.
The resulting values for 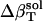 range from 2.7 × 10−6 atm−1 for trypsin to −0.83 × 10−6 atm−1 for HEW lysozyme (Table 1). Such a range in
range from 2.7 × 10−6 atm−1 for trypsin to −0.83 × 10−6 atm−1 for HEW lysozyme (Table 1). Such a range in 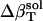 implies a nonuniform contribution from the protein surface that could arise from differences in the hydration of surface groups with different polarity.
implies a nonuniform contribution from the protein surface that could arise from differences in the hydration of surface groups with different polarity.
We use a simple, linear model to decompose 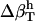 (Eq. 6), into contributions from changes in the hydration water compressibility due to charged, polar, and apolar surfaces. The volume of the hydration water is decomposed into the volume near charged surfaces, Vh-crg, the volume near polar surfaces, Vh-plr, and the volume near apolar surfaces, Vh-aplr. The corresponding volume fractions are Φh-crg = Vh-crg/Vh, Φh-plr = Vh-plr/Vh, and Φh-aplr = Vh-aplr/Vh. In a first approximation, the hydration volume fractions can be replaced by the respective surface fractions as
(Eq. 6), into contributions from changes in the hydration water compressibility due to charged, polar, and apolar surfaces. The volume of the hydration water is decomposed into the volume near charged surfaces, Vh-crg, the volume near polar surfaces, Vh-plr, and the volume near apolar surfaces, Vh-aplr. The corresponding volume fractions are Φh-crg = Vh-crg/Vh, Φh-plr = Vh-plr/Vh, and Φh-aplr = Vh-aplr/Vh. In a first approximation, the hydration volume fractions can be replaced by the respective surface fractions as 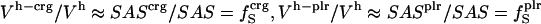 , and
, and 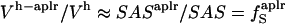 . With this approximation,
. With this approximation,  becomes
becomes
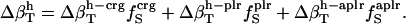 |
(14) |
Best-fitted values for 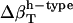 are calculated from
are calculated from 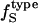 and
and 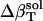 values (Table 1) by using a least-squares maximum likelihood method,
values (Table 1) by using a least-squares maximum likelihood method, 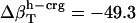 ,
, 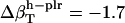 , and
, and 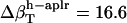 (in units of 10−6 atm−1; see Table 2). The compressibility of hydration water surrounding charged, polar, and apolar surfaces are the values
(in units of 10−6 atm−1; see Table 2). The compressibility of hydration water surrounding charged, polar, and apolar surfaces are the values 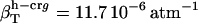 ,
, 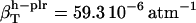 , and
, and 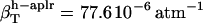 . The estimates for
. The estimates for 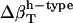 reproduce the original
reproduce the original 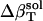 with <10% error (last row in Table 1).
with <10% error (last row in Table 1).
TABLE 2.
Local compressibilities around charged, polar, and apolar groups
| Charged | Polar | Apolar | |
|---|---|---|---|
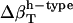 (prot)* (prot)*
|
−49.3 | −1.7 | 16.6 |
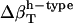 (prot-renorm)† (prot-renorm)†
|
−36.4 | −1.3 | 12.2 |
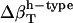 (pep)‡ (pep)‡
|
−48.5 | −6.6 | −3.4 |
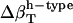 (pep-renorm)§ (pep-renorm)§
|
−35.8 | −4.9 | −2.5 |
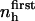 (prot) (prot) |
2.76 | 1.51 | 1.11 |
Errors estimated by maximum likelihood analysis of three proteins are 3.3% for charged, 6.3% for polar, and 0.3% for the apolar hydration compressibility.
Change in types of hydration water compressibility around proteins.
Change in types of hydration water compressibility around proteins renormalized to experimental water compressibility, 45 10−6 atm−1.
Change in types of hydration water compressibility around peptides from maximum likelihood method applied to dipeptide data from Table 4, with Φh = 0.5.
Change in hydration water compressibility around peptides renormalized to experimental water compressibility, 45 10−6 atm−1.
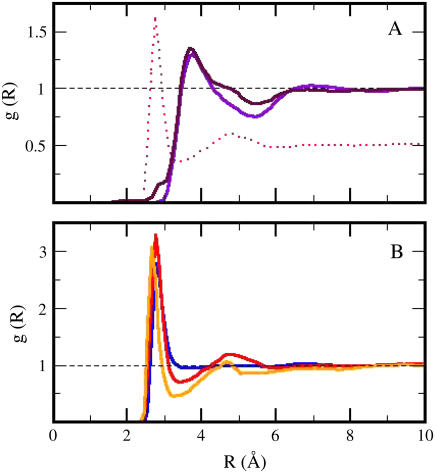
The values obtained for the compressibility of water around charged, polar, and apolar surfaces from maximum likelihood estimates indicate a clear trend: the compressibility of water hydrating charged atoms is lower than the compressibility of bulk water, the compressibility of water hydrating polar atoms is about the same as the compressibility of bulk water, and the compressibility of water surrounding apolar atoms tends to be higher than the compressibility of bulk water. The differences in hydration water compressibility for the three types of surfaces are consistent with the differences in hydration water density indicated by the corresponding RDFs (Figs. 1 and 2).
FIGURE 2.
A comparison of RDFs for apolar surfaces (A) in proteins (maroon curve) and peptides (violet curve). The red (dotted) curve in Panel A represents the scaled (by half) RDF for charged protein surfaces. Panel B represents the RDFs for charged surfaces in proteins (red curve) and peptides (orange curve). The blue curve represents the oxygen-oxygen RDF for TIP3 water.
Independent estimate of the compressibility of the first hydration shell
A qualitative check of the results obtained for the compressibility of hydration water from the decomposition of the hydration water compressibility as a function of the chemical nature of the protein-water interface can be readily obtained. In particular, the prediction that more charged protein surface induces a reduced compressibility of the water in the hydration shell of proteins can be verified by calculating the isothermal compressibility of the first hydration layer surrounding trypsin and HEW-lysozyme from MD simulations. The first hydration layer is the main contributor to the hydration shell compressibility. Use of these two proteins is instructive because they have similar fractions of exposed polar (40% and 38%) and apolar (51% and 46%) surface but different fractions of exposed charged surface (8% for trypsin and 16% for HEW-lysozyme). An alternative to Eq. 11 for compressibility used here to estimate the compressibility of hydration water is (3)
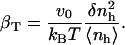 |
(15) |
The value v0 is the average volume of one water molecule in the hydration shell and 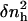 and 〈nh〉 are the fluctuations and averages of the number of hydration water molecules in the first hydration shell, nh. The value nh(t) is a time series of the number of water molecules within a shell of 3.1 Å surrounding the protein.
and 〈nh〉 are the fluctuations and averages of the number of hydration water molecules in the first hydration shell, nh. The value nh(t) is a time series of the number of water molecules within a shell of 3.1 Å surrounding the protein.
The average volume of a water molecule in the first hydration layer is estimated using the average solvent-accessible surface area, the width of the layer, and the average number of hydration waters: v0 = 〈SAS〉 × 3.1/〈nh〉. The average of v0 for the four globular proteins is 23 Å3. This value is smaller than the average volume of a water molecule in bulk, 29.7 Å3, but close to the volume of water molecules hydrating proteins obtained from high resolution crystal structures of 22 globular proteins (52), 23.8 Å3.
We calculated 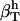 for trypsin and HEW lysozyme from 〈nh〉 = 676 for trypsin and 〈nh〉 = 456 for HEW lysozyme, the fluctuations in the number of water molecules in the first hydration shell,
for trypsin and HEW lysozyme from 〈nh〉 = 676 for trypsin and 〈nh〉 = 456 for HEW lysozyme, the fluctuations in the number of water molecules in the first hydration shell, 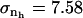 (trypsin) and 5.84 (HEW lysozyme), and the average volume of one water molecule in the hydration shell, v0. With these values, the calculated compressibility of the first hydration layer is 47.2 10−6 atm−1 for trypsin and 41.6 10−6 atm−1 for HEW lysozyme. The calculated hydration compressibility values for the first solvation layer are 77% of bulk water compressibility for trypsin and 68% of bulk water compressibility for HEW-lysozyme. The lower compressibility of the first hydration layer of HEW lysozyme relative to trypsin is consistent with the model (Eq. 14), given the difference in the charged solvent-accessible surface areas exposed by the two proteins to water. However, this is only an approximation for the compressibility of the first hydration shell and does not represent the whole hydration water compressibility. Equation 15 is strictly valid for compressibility calculation in an NVT ensemble.
(trypsin) and 5.84 (HEW lysozyme), and the average volume of one water molecule in the hydration shell, v0. With these values, the calculated compressibility of the first hydration layer is 47.2 10−6 atm−1 for trypsin and 41.6 10−6 atm−1 for HEW lysozyme. The calculated hydration compressibility values for the first solvation layer are 77% of bulk water compressibility for trypsin and 68% of bulk water compressibility for HEW-lysozyme. The lower compressibility of the first hydration layer of HEW lysozyme relative to trypsin is consistent with the model (Eq. 14), given the difference in the charged solvent-accessible surface areas exposed by the two proteins to water. However, this is only an approximation for the compressibility of the first hydration shell and does not represent the whole hydration water compressibility. Equation 15 is strictly valid for compressibility calculation in an NVT ensemble.
Application to experiment: a formula for obtaining intrinsic protein compressibility from the experimentally determined compressibility
We can now outline a simple algorithm for the calculation of protein intrinsic isothermal compressibility, 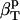 from the experimental isothermal protein compressibility,
from the experimental isothermal protein compressibility, 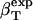 . First, one must estimate
. First, one must estimate 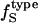 from the charged, polar, apolar, and total SAS of the three-dimensional structure of the protein. The value
from the charged, polar, apolar, and total SAS of the three-dimensional structure of the protein. The value 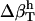 is then calculated from
is then calculated from 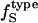 and
and 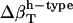 using Eq. 14. Next, protein intrinsic compressibility,
using Eq. 14. Next, protein intrinsic compressibility, 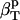 can be calculated from Eq. 9 by subtracting
can be calculated from Eq. 9 by subtracting 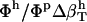 from the experimental isothermal compressibility.
from the experimental isothermal compressibility.
The algorithm can be used to decompose the experimental compressibility for any protein of known three-dimensional structure. For the application, it is necessary to reconcile the difference in the calculated and experimental isothermal compressibility of bulk water. Bulk water compressibility estimated from sound velocity measurements is 45 × 10−6 atm−1 in ambient conditions (53) while the calculated compressibility for pure water, the TIP3P model, is 61 × 10−6 atm−1. The calculated 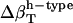 must be rescaled by a factor of 45:61 to be compatible with the experiment (Table 2).
must be rescaled by a factor of 45:61 to be compatible with the experiment (Table 2).
The use of Eq. 9 for the calculation of the intrinsic protein compressibility, 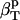 , requires an estimate of the ratio between the hydration and protein volume fractions, Φh/Φp. Here we use a simple approximation dictated by the convergence of the RDFs around protein molecules: no differences in the RDFs between the bulk water and hydration water can be observed at distances, D, larger than 8 Å from the protein surface (Figs. 1 and 2). For a globular protein with a radius of gyration, Rgyr, the ratio between the hydration and protein volumes can be approximated by
, requires an estimate of the ratio between the hydration and protein volume fractions, Φh/Φp. Here we use a simple approximation dictated by the convergence of the RDFs around protein molecules: no differences in the RDFs between the bulk water and hydration water can be observed at distances, D, larger than 8 Å from the protein surface (Figs. 1 and 2). For a globular protein with a radius of gyration, Rgyr, the ratio between the hydration and protein volumes can be approximated by
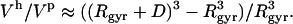 |
For a typical protein, with Rgyr = 15 Å and D = 8 Å, the Φh/Φp ratio is 2.6.
NMR absorption equilibrium experiments (54) have found that for HEW-lysozyme, the onset of drastic decrease in relaxation rate occurs at 1.7 g of water for 1 g of protein. If the water density is 1 g/cm3 and protein density is 1.43 g/cm3, Φh/Φp = 1.7 × 1.43 = 2.43. The ratio of Φh/Φp obtained using the guidelines provided by the RDFs is in good agreement with estimates from NMR experiments. Both methods estimate that hydration of a regular protein such as lysozyme requires a hydration water volume that is approximately two-and-a-half times larger than the protein volume.
Examples
The method is illustrated using three proteins of known structure: lysozyme, α-lactalbumin, and myoglobin. The value 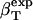 have been estimated by Gekko and Hasegawa using Eq. 8 (38). The
have been estimated by Gekko and Hasegawa using Eq. 8 (38). The 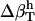 values are estimated here using the adjusted (to experiment)
values are estimated here using the adjusted (to experiment) 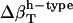 from Table 2 and the corresponding fractions of protein-water interfaces,
from Table 2 and the corresponding fractions of protein-water interfaces, 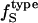 . To obtain the intrinsic protein compressibility we estimate the corrections due to protein hydration using the ratio of Φh/Φp = 2.43. This leads to intrinsic compressibility corrections ranging from 1.13 10−6 atm−1 for α-lactalbumin and 4.37 10−6 atm−1 for myoglobin. Final protein intrinsic compressibilities are listed in Table 3.
. To obtain the intrinsic protein compressibility we estimate the corrections due to protein hydration using the ratio of Φh/Φp = 2.43. This leads to intrinsic compressibility corrections ranging from 1.13 10−6 atm−1 for α-lactalbumin and 4.37 10−6 atm−1 for myoglobin. Final protein intrinsic compressibilities are listed in Table 3.
TABLE 3.
Examples: the calculation of protein intrinsic isothermal compressibility from experimental compressibility
| α-Lactalbumin | Lysozyme | Myoglobin | |
|---|---|---|---|
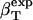 |
12.4 | 7.73 | 11.2 |
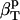 (δV2)* (δV2)*
|
11.8 | 10.2 | — |
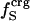 (%) (%) |
18 | 16 | 20 |
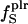 (%) (%) |
29 | 38 | 30 |
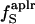 (%) (%) |
53 | 46 | 50 |
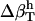 |
−0.46 | −0.71 | −1.8 |
2.43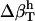
|
−1.12 | −1.72 | −4.37 |
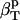 † †
|
13.5 | 9.5 | 17.5 |
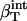 is protein intrinsic compressibility calculated from volume fluctuations (44) for α-lactalbumin and lysozyme.
is protein intrinsic compressibility calculated from volume fluctuations (44) for α-lactalbumin and lysozyme.
 is the intrinsic compressibility calculated from experimental data including the hydration contribution.
is the intrinsic compressibility calculated from experimental data including the hydration contribution.
The first two proteins considered here, lysozyme and α-lactalbumin, are part of the set of proteins for which the intrinsic isothermal compressibility was calculated from volume fluctuations in MD simulations (44) (Table 3). The intrinsic protein compressibilities calculated from experimental data are in good agreement with the intrinsic compressibility calculated from molecular volume fluctuations, 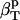 (δV2) (Table 3) (44) with a relative error of 7% for lysozyme and 12% for α-lactalbumin. For myoglobin, our method predicts a large contribution to the intrinsic isothermal compressibility from hydration, 4.4 10−6 atm−1. This estimate remains to be verified through other methods.
(δV2) (Table 3) (44) with a relative error of 7% for lysozyme and 12% for α-lactalbumin. For myoglobin, our method predicts a large contribution to the intrinsic isothermal compressibility from hydration, 4.4 10−6 atm−1. This estimate remains to be verified through other methods.
The match between the intrinsic protein compressibility calculated from molecular volume fluctuations and from estimates of hydration contributions to protein compressibility provides a first validation of the theoretical model for protein hydration compressibility.
Hydration water compressibility around small compounds
Others have discussed the possibility that the hydration characteristics of atomic groups at the protein surface can be modeled from hydration properties of similar groups in small molecules. It was proposed that protein hydration water compressibility can be estimated from the hydration water compressibility of small compounds (39,55,56), but the idea was challenged on the basis that the environment of basic groups in proteins is different from that of small molecules in solution or, alternatively, because the charged groups in proteins may not be as exposed to the solvent as those in small molecules ((7) and references therein). The calculation of hydration water compressibility from MD simulations offers the opportunity for a direct evaluation of this proposal.
We determine the solution compressibility of four dipeptides in water, 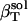 , from whole system volume fluctuations and the predicted solution compressibility,
, from whole system volume fluctuations and the predicted solution compressibility, 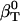 , based on volume fraction of water and peptide solute. Values for 〈SAS〉crg, 〈SAS〉plr, 〈SAS〉aplr, and total 〈SAS〉, their respective fractions, as well as peptide and simulation box volumes for small compounds, are presented in Table 4. The intrinsic compressibility is very small for peptides because of the insignificant amount of interstitial space shielded from water, the major source of intrinsic compressibility (44), and the negligible compressibility of the covalent bonds (4). The
, based on volume fraction of water and peptide solute. Values for 〈SAS〉crg, 〈SAS〉plr, 〈SAS〉aplr, and total 〈SAS〉, their respective fractions, as well as peptide and simulation box volumes for small compounds, are presented in Table 4. The intrinsic compressibility is very small for peptides because of the insignificant amount of interstitial space shielded from water, the major source of intrinsic compressibility (44), and the negligible compressibility of the covalent bonds (4). The 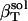 and other values calculated from the simulations are shown in Table 4 for four dipeptides: alanine, glutamic, aspartic, and lysine dipeptides. For all four compounds, the dipeptide volume fraction, Φp, is small, ∼2% of the total solution volume and Φw is 98%. The term
and other values calculated from the simulations are shown in Table 4 for four dipeptides: alanine, glutamic, aspartic, and lysine dipeptides. For all four compounds, the dipeptide volume fraction, Φp, is small, ∼2% of the total solution volume and Φw is 98%. The term 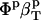 ≈ 0.0 and the main contributions to the predicted solution compressibility are from water,
≈ 0.0 and the main contributions to the predicted solution compressibility are from water, 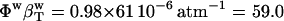 .
. 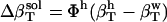 for the four small compounds are listed in Table 4.
for the four small compounds are listed in Table 4.
TABLE 4.
Small compounds solution compressibility, 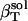 , calculated from simulation box volume fluctuations,
, calculated from simulation box volume fluctuations, 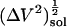 , and average, 〈V〉sol
, and average, 〈V〉sol
| Alad | Aspd | Glud | Lysd | |
|---|---|---|---|---|
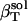 |
57 | 51 | 53 | 54 |
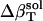 * *
|
−2 | −8 | −6 | −5 |
| 〈SAS〉crg | 0 | 97 | 98 | 59 |
| 〈SAS〉plr | 95 | 88 | 88 | 90 |
| 〈SAS〉aplr | 280 | 230 | 257 | 333 |
| 〈SAS〉 | 375 | 416 | 445 | 482 |
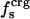 (%) (%) |
0 | 23 | 22 | 12 |
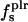 (%) (%) |
25 | 21 | 20 | 19 |
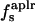 (%) (%) |
75 | 56 | 58 | 69 |
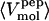 (Å3) (Å3) |
479 | 545 | 600 | 669 |
| 〈Vsol〉 (Å3) | 32,819 | 32,650 | 32,665 | 32,777 |
Error 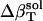 (%)† (%)†
|
1 | 1 | 5 | 2 |
Compressibilities are reported as 10−6 atm−1.
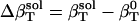 .
.
Errors in the calculation of residual hydration water compressibility from the estimated changes in hydration water compressibility: 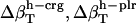 , and
, and 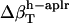 .
.
The 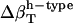 was estimated for the four dipeptides using
was estimated for the four dipeptides using 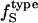 and
and 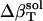 shown in Table 4, and Φh = 0.5. The optimized values (Table 2) for
shown in Table 4, and Φh = 0.5. The optimized values (Table 2) for 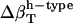 from the dipeptides for our small compounds are as follows:
from the dipeptides for our small compounds are as follows: 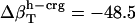 ,
, 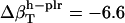 , and
, and 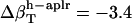 (in units of 10−6 atm−1). After normalization with experimental isothermal compressibility of bulk water,
(in units of 10−6 atm−1). After normalization with experimental isothermal compressibility of bulk water, 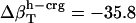 ,
, 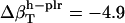 , and
, and 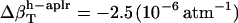 , and the isothermal compressibilities of water near peptide surfaces are
, and the isothermal compressibilities of water near peptide surfaces are 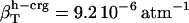 ,
, 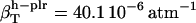 , and
, and 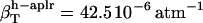 . For small compounds, the compressibility of the hydration water surrounding all types of atomic groups is lower than the compressibility of bulk water. The ranking among types of hydration water compressibility is the same as that for proteins in that
. For small compounds, the compressibility of the hydration water surrounding all types of atomic groups is lower than the compressibility of bulk water. The ranking among types of hydration water compressibility is the same as that for proteins in that 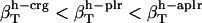 . The estimated values for hydration water compressibility around the dipeptides studied here reproduce
. The estimated values for hydration water compressibility around the dipeptides studied here reproduce 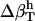 with <5% error (calculated errors are listed in Table 4).
with <5% error (calculated errors are listed in Table 4).
The 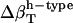 estimates for the dipeptides agree qualitatively with various experimental estimates for small compounds (4,57). It was found that at 25°C the charged amino
estimates for the dipeptides agree qualitatively with various experimental estimates for small compounds (4,57). It was found that at 25°C the charged amino  and carboxyl-COO− contribute have large negative partial molar adiabatic compressibility, −34 cm3 mol−1 atm−1. By contrast, for uncharged species, the partial molar adiabatic compressibility could be either positive (2.74 cm3 mol−1 atm−1 for glycolamide and 1 cm3 mol−1 atm−1 for the peptide −CONH− group) or negative (−2 cm3 mol−1 atm−1 for the −OH groups in pentoses and hexoses, and −12.5 cm3 mol−1 atm−1 for ribose).
and carboxyl-COO− contribute have large negative partial molar adiabatic compressibility, −34 cm3 mol−1 atm−1. By contrast, for uncharged species, the partial molar adiabatic compressibility could be either positive (2.74 cm3 mol−1 atm−1 for glycolamide and 1 cm3 mol−1 atm−1 for the peptide −CONH− group) or negative (−2 cm3 mol−1 atm−1 for the −OH groups in pentoses and hexoses, and −12.5 cm3 mol−1 atm−1 for ribose).
Hydration properties of proteins and peptides
A comparison between the changes in hydration water compressibility around proteins and dipeptides reveals that the charged groups, and to a lesser extent the polar groups, are hydrated similarly in proteins and dipeptides, both exhibiting a decrease in the hydration water compressibility with respect to bulk water. Apolar groups have opposite sign contributions in proteins and dipeptides, with an increase in hydration water compressibility around apolar groups in proteins.
The two sets of 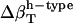 (Table 2) cannot be transferred between proteins and peptides. We have calculated errors in
(Table 2) cannot be transferred between proteins and peptides. We have calculated errors in 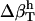 for proteins using the values
for proteins using the values 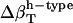 from dipeptides and, inversely, we attempted to reproduce the
from dipeptides and, inversely, we attempted to reproduce the 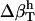 for dipeptides using the
for dipeptides using the 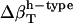 for proteins. Errors larger than 20% were obtained in all trials, with particularly large errors in the
for proteins. Errors larger than 20% were obtained in all trials, with particularly large errors in the 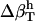 of proteins when using
of proteins when using 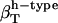 from dipeptides. One possible explanation for the differences in the compressibility of hydration contributions of same surface types in proteins and small compounds is the intrinsic differences in the size of the molecules (which translates into a significantly large difference of the curvature of the solute-water interface) and the particular local arrangements of adjacent charged, polar, and apolar surfaces in proteins. Based on the results presented here, we conclude that the hydration properties of native globular proteins cannot be modeled using small molecule data. Therefore, even though the charged, polar, and apolar contributions to hydration compressibility for small compounds are ranked the same way as those in proteins (
from dipeptides. One possible explanation for the differences in the compressibility of hydration contributions of same surface types in proteins and small compounds is the intrinsic differences in the size of the molecules (which translates into a significantly large difference of the curvature of the solute-water interface) and the particular local arrangements of adjacent charged, polar, and apolar surfaces in proteins. Based on the results presented here, we conclude that the hydration properties of native globular proteins cannot be modeled using small molecule data. Therefore, even though the charged, polar, and apolar contributions to hydration compressibility for small compounds are ranked the same way as those in proteins (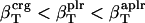 ), their magnitude is different for proteins and small compounds and the results are not interchangeable.
), their magnitude is different for proteins and small compounds and the results are not interchangeable.
RDFs of water molecules around proteins and small dipeptides
The perturbation of the water structure around small molecules is compared to that around proteins by consideration of the RDFs in Fig. 2. While several common features exist, significant differences are also observed. One characteristic aspect of the small molecule RDFs is that the structuring of water extends to 10–12 Å from each given atom in the dipeptide. For proteins, there is no noticeable water structuring extending beyond 8–10 Å from the protein surface. One possible explanation is that for proteins, long-range structuring of water is averaged out by the overlapping hydration shells originating in the adjacent charged, polar, and apolar surfaces.
The main differences between the RDFs from apolar surfaces (Fig. 2 A) in proteins (maroon curve) and dipeptides (violet curve) are the two shoulders at short (2.7 Å) and intermediate (4.8 Å) distance in the RDF of the apolar surface of proteins. The scaled (by 1:2) RDF from the charged protein surfaces, the red (dotted) curve in panel A, is also shown in Fig. 2, to indicate that the positions of the shoulders in the RDFs from the protein apolar surface coincide with the positions of the peaks in the RDFs from the charged surface. The RDFs of water surrounding apolar surfaces are modulated by contributions from water molecules in proximity of charged surfaces in proteins, a direct effect of adjacent and intertwining charged and apolar protein surface patches on the protein solvent-accessible surface. The net result is an overlap in the hydration shells of adjacent apolar and charged solvent-accessible surface areas.
Fig. 2 B represents the RDFs for charged surfaces in proteins (red curve) and peptides (orange curve). The blue curve represents the oxygen-oxygen RDF for TIP3 water. The location of the first hydration shells is displaced by .1 Å in proteins with respect to peptides, i.e., the first water oxygen is in average closer to the peptide surface than to the protein surface, a possible consequence of the different curvature at the solute-solvent interface (with a smaller curvature for the protein surface). The second peaks are located at roughly the same distance, 4.7 Å, but the shape and the width of the peaks are different.
Differences in the specific charged, polar, and apolar hydration in proteins and small peptides originate from both chemistry and the local topology and geometry of the solvent-accessible surface. The overall curvature of the solvent-accessible surface for a 150-residue protein is ∼1:15 Å−1 and much larger, 1:3.5 Å−1, for dipeptides. The local geometry at the protein-water interface is either convex or concave, corresponding to peaks and valleys on the protein solvent-accessible surface. As a general trend, the charged groups will tend to be on the peaks and the apolar groups on the valleys. Because of their smaller size, this tendency is less strictly followed for small peptides. Global and local differences in the geometry of the solvent-accessible surfaces between proteins and peptides are partially responsible for the fact that data from small compounds cannot be used to estimate the compressibility of water surrounding the protein.
DISCUSSION
The role of hydration and intrinsic protein flexibility in modulating protein stability, conformational dynamics, and protein-ligand binding can be better assessed when contributions from hydration water are well understood and easy to estimate. In this study we found that the compressibility of protein hydration shell is a function of the complex chemical nature of the protein-water interface: the water surrounding charged atomic groups in proteins has lower compressibility than bulk water and on the same order of magnitude as protein intrinsic compressibility; the compressibility of water surrounding polar atomic groups is about the same as bulk water compressibility; and the compressibility of water surrounding apolar atomic groups is higher than that of bulk water, 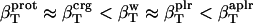 .
.
From investigations of hydration characteristics of atomic groups at the surface of similar groups in small molecules, we find that the compressibility of protein hydration water can only be assessed from protein-based additive contributions from charged, polar, and apolar surfaces. These contributions are specific to proteins and cannot be modeled based on similar data obtained for small molecules.
Using the detailed information from MD simulations, we have outlined a protocol for separating intrinsic protein and hydration water contributions to experimental compressibility obtained from sound velocity measurements. The formulation in Eq. 14 allows for the intrinsic protein compressibility to be calculated using the chemically specific 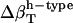 and the fractions of charged, polar, and apolar SASA for any protein of known three-dimensional structure.
and the fractions of charged, polar, and apolar SASA for any protein of known three-dimensional structure.
Our analysis of hydration contribution to protein intrinsic compressibility is similar in spirit to that of Breslauer and co-workers (13). These authors have determined hydration contributions from cross-correlating thermodynamic and structural data for globular proteins. Our formulation combines information from protein volume fluctuations and the radial distribution functions of water around protein and small molecules to arrive at a simple and easy to implement formula for the intrinsic protein compressibility, while the changes in the compressibility of hydration water are explicitly included.
Interpretation of experimental data on compressibility change due to protein conformational transitions and protein-ligand binding (6) can benefit from the formulation presented here. It is a matter of estimating the change in each type of accessible surface area. As an example, in a detailed experimental investigation of the change in the partial specific adiabatic compressibility of globular proteins, Chalikian and Breslauer (5) show that the partial specific adiabatic compressibility of globular proteins decreases upon unfolding. A decrease in the compressibility is also observed in the native to partially unfolded transition, while the transition to a compact intermediate state results in an increase in compressibility. The behavior may be rationalized from our model of hydration compressibility. When the protein unfolds, a large fraction of the previously buried apolar surface is exposed to water. The newly created hydration water layer surrounding the freshly exposed apolar groups has a higher compressibility than bulk water. The effect is a net increase in the compressibility of the hydration water and a decrease in the negative component of hydration contribution to the total compressibility change. Because the intrinsic contribution to the compressibility of the protein unfolded state is practically negligible, the sole contribution to solution compressibility is the hydration water compressibility. The 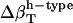 and the unfolded state
and the unfolded state 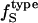 allow for an estimate of the compressibility of the protein in the unfolded state for any protein of known sequence.
allow for an estimate of the compressibility of the protein in the unfolded state for any protein of known sequence.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
This work was partially supported by grants from the U.S. National Institutes of Health (AI39639 to C.B.P.) and the Sloan Foundation and Department of Energy (to V.M.D.).
References
- 1.Raschke, T. M. 2006. Water structure and interactions with protein surfaces. Curr. Opin. Struct. Biol. 16:152–159. [DOI] [PubMed] [Google Scholar]
- 2.Eden, D., J. B. Matthew, J. J. Rosa, and F. M. Richards. 1982. Increase in apparent compressibility of cytochrome c upon oxidation. Proc. Natl. Acad. Sci. USA. 79:815–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Phelps, D. K., and C. B. Post. 1995. A novel basis for capsid stabilization by antiviral compounds. J. Mol. Biol. 254:544–551. [DOI] [PubMed] [Google Scholar]
- 4.Chalikian, T. V., A. P. Sarvazyan, and K. J. Breslauer. 1994. Hydration and partial compressibility of biological compounds. Biophys. Chem. 51:89–109. [DOI] [PubMed] [Google Scholar]
- 5.Chalikian, T. V., and K. J. Breslauer. 1996. Compressibility as a means to detect and characterize globular protein states. Proc. Natl. Acad. Sci. USA. 93:1012–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gekko, K. 2002. Compressibility gives new insight into protein dynamics and enzyme function. Biochim. Biophys. Acta. 1595:382–386. [DOI] [PubMed] [Google Scholar]
- 7.Chalikian, T. V. 2003. Volumetric properties of proteins. Annu. Rev. Biophys. Biomol. Struct. 32:207–235. [DOI] [PubMed] [Google Scholar]
- 8.Gekko, K., A. Kimoto, and T. Kamiyama. 2003. Effects of disulfide bonds on compactness of protein molecules revealed by volume, compressibility, and expansibility changes during reduction. Biochemistry. 42:13746–13753. [DOI] [PubMed] [Google Scholar]
- 9.Taulier, N., I. V. Beletskaya, and T. V. Chalikian. 2005. Compressibility changes accompanying conformational transitions of apomyoglobin. Biopolymers. 79:218–229. [DOI] [PubMed] [Google Scholar]
- 10.Dubins, D. N., R. Filfil, R. B. Macgregor, and T. V. Chalikian. 2003. Volume and compressibility changes accompanying thermally induced native-to-unfolded and molten globule-to-unfolded transitions of cytochrome c: A high pressure study. Biochemistry. 42:8671–8678. [DOI] [PubMed] [Google Scholar]
- 11.Chalikian, T. V., and R. Filfil. 2003. The thermodynamics of protein-protein recognition as characterized by a combination of volumetric and calorimetric techniques: the binding of turkey ovomucoid third domain to alpha-chymotrypsin. J. Mol. Biol. 326:1271–1288. [DOI] [PubMed] [Google Scholar]
- 12.Jung, C. 2002. Cytochrome p-450-co and substrates: lessons from ligand binding under high pressure. Biochim. Biophys. Acta. 1595:309–328. [DOI] [PubMed] [Google Scholar]
- 13.Chalikian, T. V., M. Totrov, R. Abagyan, and K. J. Breslauer. 1996. The hydration of globular proteins as derived from volume and compressibility measurements: cross correlating thermodynamic and structural data. J. Mol. Biol. 260:588–603. [DOI] [PubMed] [Google Scholar]
- 14.Dadarlat, V. M., and C. B. Post. 2003. Adhesive-cohesive model for protein compressibility: an alternative perspective on stability. Proc. Natl. Acad. Sci. USA. 100:14778–14783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Steinbach, P., and B. Brooks. 1993. Protein hydration elucidated by molecular dynamics simulation. Proc. Natl. Acad. Sci. USA. 90:9135–9139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schroder, C., T. Rudas, S. Boresch, and O. Steinhauser. 2006. Simulation studies of the protein-water interface. I. Properties at the molecular resolution. J. Chem. Phys. 124:234907. [DOI] [PubMed] [Google Scholar]
- 17.Rudas, T., C. Schroder, S. Boresch, and O. Steinhauser. 2006. Simulation studies of the protein-water interface. II. Properties at the mesoscopic resolution. J. Chem. Phys. 124:234908. [DOI] [PubMed] [Google Scholar]
- 18.Vitkup, D., D. Ringe, G. A. Petsko, and M. Karplus. 2000. Solvent mobility and the protein “glass” transition. Nat. Struct. Biol. 7:34–38. [DOI] [PubMed] [Google Scholar]
- 19.Rupley, J. A., and G. Careri. 1991. Protein hydration and function. Adv. Protein Chem. 41:37–172. [DOI] [PubMed] [Google Scholar]
- 20.Pollack, G. H. 2001. Is the cell a gel—and why does it matter? Jpn. J. Physiol. 51:649–660. [DOI] [PubMed] [Google Scholar]
- 21.Pollack, G. H. 2003. The role of aqueous interfaces in the cell. Adv. Colloid Interface Sci. 103:173–196. [DOI] [PubMed] [Google Scholar]
- 22.Brunne, R. M., E. Liepinsh, G. Otting, K. Wuthrich, and W. F. van Gunsteren. 1993. Hydration of proteins: a comparison of experimental residence times of water molecules solvating the bovine pancreatic trypsin inhibitor with theoretical model calculations. J. Mol. Biol. 231:1040–1048. [DOI] [PubMed] [Google Scholar]
- 23.Badger, J. 1993. Multiple hydration layers in cubic insulin crystals. Biophys. J. 65:1656–1659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Svergun, D. I., S. M. Richard, H. J. Koch, Z. Sayers, S. Kuprin, and G. Zaccai. 1998. Protein hydration in solution: experimental observation by x-ray and neutron scattering. Proc. Natl. Acad. Sci. USA. 95:2267–2272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Venu, K., L. A. Svensson, and B. Halle. 1999. Orientational order and dynamics of hydration water in a single crystal of bovine pancreatic trypsin inhibitor. Biophys. J. 77:1074–1085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Russo, D., G. Hura, and T. Head-Gordon. 2005. Hydration dynamics near a model protein surface. Biophys. J. 86:1852–1862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Levitt, M., and R. Sharon. 1988. Accurate simulation of protein dynamics in solution. Proc. Natl. Acad. Sci. USA. 85:7557–7561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Makarov, V. A., K. A. Andrews, and B. M. Pettitt. 1998. a. Protein hydration density: theory, simulation and crystallography. Curr. Opin. Struct. Biol. 8:218–221. [DOI] [PubMed] [Google Scholar]
- 29.Makarov, V. A., K. A. Andrews, and B. M. Pettitt. 1998. b. Reconstructing the protein-water interface. Biopolymers. 45:469–478. [DOI] [PubMed] [Google Scholar]
- 30.Makarov, V. A., B. K. Andrews, P. E. Smith, and B. M. Pettitt. 2000. Residence times of water molecules in the hydration sites of myoglobin. Biophys. J. 79:2966–2974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Henchman, R. H., and J. A. McCammon. 2002. Structural and dynamic properties of water around acetylcholinesterase. Protein Sci. 11:2080–2090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Halle, B., and M. Davidovic. 2003. Biomolecular hydration: from water dynamics to hydrodynamics. Proc. Natl. Acad. Sci. USA. 100:12135–12140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pratt, L. R., and D. Chandler. 1977. Theory of the hydrophobic effect. J. Chem. Phys. 67:3683–3704. [Google Scholar]
- 34.Lazaridis, T., and M. E. Paulaitis. 1992. Entropy of hydrophobic hydration: a new statistical mechanical formulation. J. Chem. Phys. 96:3847. [Google Scholar]
- 35.Lazaridis, T., and M. E. Paulaitis. 1994. Simulation studies of the hydration entropy of simple, hydrophobic solutes. J. Phys. Chem. 98:635. [Google Scholar]
- 36.Hummer, G., S. Garde, A. E. García, and L. R. Pratt. 2000. New perspectives on hydrophobic effects. Chem. Phys. 258:349–370. [Google Scholar]
- 37.Lee, B. 1983. Calculation of volume fluctuation for globular protein models. Proc. Natl. Acad. Sci. USA. 80:622–626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gekko, K., and Y. Hasegawa. 1986. Compressibility structure relationship of globular-proteins. Biochemistry. 25:6563–6571. [DOI] [PubMed] [Google Scholar]
- 39.Kharakoz, D. P., and A. P. Sarvazyan. 1993. Hydrational and intrinsic compressibilities of globular proteins. Biopolymers. 33:11–26. [DOI] [PubMed] [Google Scholar]
- 40.Chalikian, T. V., and K. J. Breslauer. 1998. Thermodynamic analysis of biomolecules: a volumetric approach. Curr. Opin. Struct. Biol. 8:657–664. [DOI] [PubMed] [Google Scholar]
- 41.Chalikian, T. V. 2001. Structural thermodynamics of hydration. J. Phys. Chem. B. 105:12566–12578. [Google Scholar]
- 42.Marchi, M. 2003. Compressibility of cavities and biological water from Voronoi volumes in hydrated proteins. J. Phys. Chem. B. 107:6598–6602. [Google Scholar]
- 43.Burling, F. T., W. I. Weis, K. M. Flaherty, and A. T. Brünger. 1996. Direct observation of protein solvation and discrete disorder with experimental crystallographic phases. Science. 271:72–77. [DOI] [PubMed] [Google Scholar]
- 44.Dadarlat, V. M., and C. B. Post. 2001. Insights into protein compressibility from molecular dynamics simulations. J. Phys. Chem. B. 105:715–724. [Google Scholar]
- 45.Gavish, B., E. Gratton, and C. J. Hardy. 1983. Adiabatic compressibility of globular proteins. Proc. Natl. Acad. Sci. USA. 80:750–754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Paci, E., and M. Marchi. 1996. Intrinsic compressibility and volume compression in solvated proteins by molecular dynamics simulations at high pressure. Proc. Natl. Acad. Sci. USA. 93:11609–11614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Darden, T. A., D. M. York, and L. G. Pedersen. 1993. Particle mesh Ewald: An nlog(n) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 48.Brooks, B., R. Bruccoleri, B. Olafson, D. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 49.Dadarlat, V. M. 2005. Potentials of mean force (PMFs) for the interaction of blocked alanine dipeptide molecules in water and vacuum from MD simulations. Biophys. J. 89:1433–1445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lee, B., and F. M. Richards. 1971. The interpretation of protein structures: estimation of static accessibility. J. Mol. Biol. 55:379–400. [DOI] [PubMed] [Google Scholar]
- 51.Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- 52.Gerstein, M., and C. Chothia. 1996. Packing at the protein-water interface. Proc. Natl. Acad. Sci. USA. 93:10167–10172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Weast, R. C. 1989. Handbook of Chemistry and Physics, 70th Ed. CRC Press, Boca Raton, FL.
- 54.Lioutas, T. S., I. C. Baianu, and M. P. Steinberg. 1986. Oxygen-17 and deuterium nuclear magnetic resonance studies of lysozyme hydration. Arch. Biochem. Biophys. 247:68–75. [DOI] [PubMed] [Google Scholar]
- 55.Iqbal, M., and R. E. Verrall. 1987. Volumetric properties of aqueous solutions of bovine serum albumin, human serum albumin, and human hemoglobin. J. Phys. Chem. 91:1935–1941. [Google Scholar]
- 56.Lockwood, D. M., P. J. Rossky, and R. M. Levy. 2000. Functional group contributions to partial molar compressibilities of alcohols in water. J. Phys. Chem. B. 104:4210–4217. [Google Scholar]
- 57.Taulier, N., and T. V. Chalikian. 2002. Compressibility of protein transitions. Biochim. Biophys. Acta. 1595:48–70. [DOI] [PubMed] [Google Scholar]