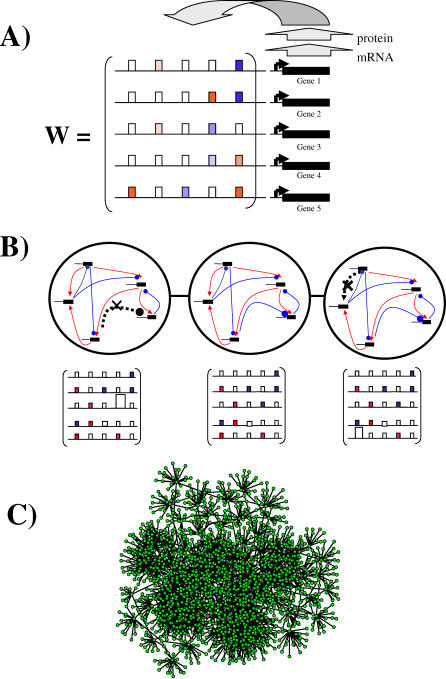
Figure 1. Regulatory Network Model and the Metagraph Concept.

(A) A transcriptional regulation network. Solid black bars indicate genes that encode transcriptional regulators in a hypothetical five-gene network or gene circuit. Each gene's expression state is influenced by the transcriptional regulators in the network. This influence is usually exerted by binding of a transcriptional regulator to a gene's regulatory region (horizontal line). The model represents the regulatory interactions between transcription factor j and genes i through a matrix w = (w_ij). A regulator's effect can be activating (w_ij > 0, red rectangles) or repressing (w_ij < 0, blue rectangles). Any given gene's expression may be unaffected by most regulators in the network (w_ij = 0, open rectangles). The different hues of red and blue correspond to different magnitudes of w_ij. The highly regular correspondence of matrix entries to binding sites serves the purpose of illustration. We note that transcription factor binding sites often function regardless of their position in a regulatory region.

(B) Gradual evolutionary changes and the metagraph. The middle panel shows a hypothetical network of five genes (top) and its matrix of regulatory interactions w (bottom), if genes are numbered clockwise from the uppermost gene. Red arrows indicate activating interactions and blue lines terminating in a circle indicate repressive interactions. The left-most network and the middle one differ in one repressive interaction from gene four to gene three (dashed gray line, black cross, large open rectangle). The right-most network and the middle one differ in one activating interaction from gene one to gene five (dashed line, black cross, large open rectangle). Each of the three network topologies corresponds to one node in a metagraph of network topologies, which is indicated by the large circle around the networks. These circles are connected because the respective networks are neighbors in the metagraph, i.e., they differ by one regulatory interaction.

(C) Part of a metagraph for a regulatory network with N = 4 genes. Each node corresponds to a network of a given topology, and two nodes are connected by an edge if they differ at one regulatory interaction (M ≈ 0.5 N² regulatory interactions, and Hamming distance of S(0) and S _∞ of d = 0.5). The metagraph in this case is connected, and the number of edges incident on a node is highly variable. The graph shown includes all viable networks that differ at no more than four regulatory interactions from an arbitrary node in the metagraph. Note that metagraphs typically have a huge number of nodes. The number of nodes in a metagraph can be counted because different nodes differ only in the signs of their regulatory interactions.