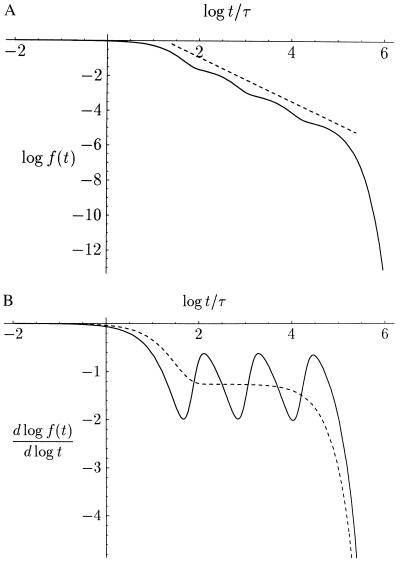
Figure 2.

(A) Decadic, double-logarithmic plot of the Markoff chain (Eq. 3) for n = 4, α = 0.5, and λ = 15. For short times t ≪ λτ, the power-law is terminated by the initial value; for long times t ≫ λ^Nτ, a fast exponential decay takes over. The power-law trend has the slope 1 + μ = 1 + |lnα|/lnλ ≈ 1.26, according to τ_n+1/τ_n = λ. The dashed line corresponds to a power-law ∝ t^−1.26. (B) Logarithmic derivative of the functions in A. The oscillations are clearly pronounced and wiggle around the dashed line representing the trend without the cosine function (second term in the braces of Eq. 6). The spacing of the humps is logλ ≈ 1.2 (τ_n+1/τ_n = λ). The plateau value is −1 −logα/logλ ≈ −1.26.