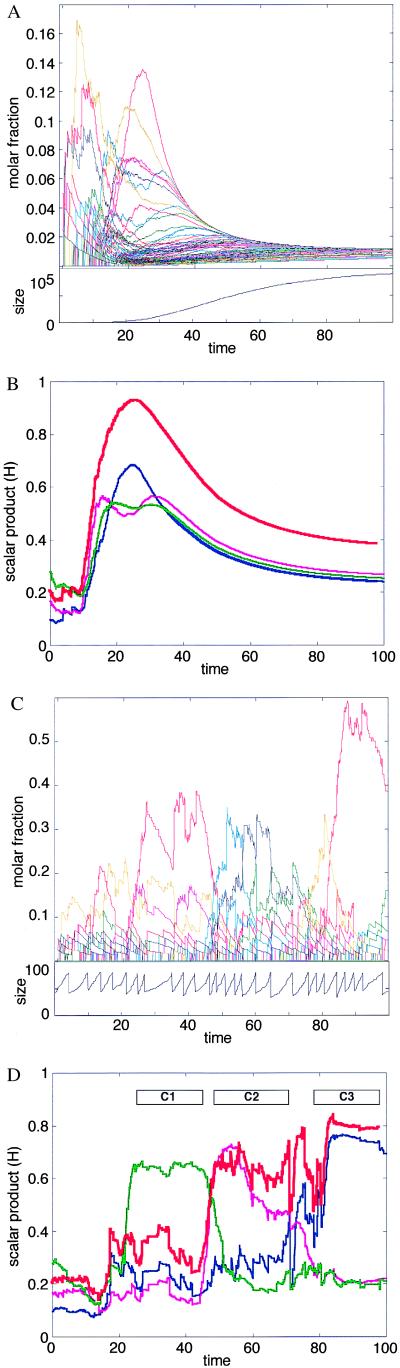
Figure 1.

Results of computer simulations for the kinetics of spontaneous aggregation in amphiphilic assemblies. An initial assembly was seeded randomly by choosing N_min individual molecules out of a pool containing n_TOT molecules of each of N_G possible types. Here N_G = 100, n_TOT = 1,000, N_min = 40. A Monte Carlo type method was used for performing discrete stochastic changes in the assembly, as dictated by Eq. 4, and by using methods as described (68). At each time step, the change in the count of molecules of each species (Δn_i) was calculated by random sampling from a Poisson distribution with average F_i(n)Δt, where Δt defines the time scale of the process. In the results presented here Δt = 0.05 sec. The logarithms of the rate enhancement factors β_ij were sampled from a normal distribution [used as a continuous approximation for the binomial distribution (57)] with an average μ = −4 and a SD σ = 4. These numerical parameter values were selected so that the resultant rate enhancement would conform with an experimentally based distribution derived from multiple reported data sets for lipid micelle catalysis (52). The molar fractions of free molecules of kind i is defined as ρ_i = (n_TOT − n_i)/N_G. For the forward and backward reaction rates we use the values k_f = 10^-2 and k_b = 10^-5 sec^-1 (for simplicity, all molecules are assumed to have identical uncatalyzed rate constants, and to differ only in their mutual rate enhancement properties). The program was written for matlab, version 5 (Mathworks, Natick, MA). The detailed results of the computer simulations are available on line at http://ool.weizmann.ac.il/PNAS2000. (A) The time dependence of the molar fraction n_i/N for each species i, in an assembly whose growth is limited only by the finite supply of molecules (Upper). Because all of the species are thermodynamically equivalent, they reach the same molar fraction after a certain time. In the transient the random network of mutual rate enhancements determines significant and nontrivial differences among the various molecular types. The change of assembly size N with time is shown (Lower): the initial increase is nearly exponential, leveling off to zero growth as the external molecular supply is exhausted and equilibrium is reached. (B) The change of the similarity values H (Eq. 2) with time. The red line depicts H values relative to the asymptotic composition n* reached by an assembly that forms and expands indefinitely with unlimited supply of all molecular species n_i. n* represents the asymptotic steady-state solution of Eq. 4. The three thin lines measure the similarity to the three main composomes of Fig. 3. (C) The time-dependent behavior of a system similar to that in A and B, but with an added process of splitting the assembly when its size reaches 2N_min. The splitting is performed by randomly dividing such an assembly into two daughter assemblies of size ≈N_min each. The count of each molecular species in a daughter assembly is sampled from a binomial distribution with n_i trials and probability 0.5. In addition, a constant population condition (11) is implemented by decomposing one randomly selected assembly after each splitting event. This is done by breaking the chosen assembly into its monomeric constituents and replenishing the external species concentrations ρ_i. The change of assembly size N with time, indicating the periodical splits, is shown (Lower). (D) The analysis of H relative to specific compositions for the same simulation shown in C. The initial random assembly proceeds through relatively abrupt transitions from one composome to another. Composomes are marked as C1 (green), C2 (magenta), and C3 (blue) (see Fig. 3).