The role of cells refractory to productive infection in acute hepatitis B viral dynamics

Abstract

During acute hepatitis B virus (HBV) infection viral loads reach high levels (≈10¹⁰ HBV DNA per ml), and nearly every hepatocyte becomes infected. Nonetheless, ≈85–95% of infected adults clear the infection. Although the immune response has been implicated in mediating clearance, the precise mechanisms remain to be elucidated. As infection clears, infected cells are replaced by uninfected ones. During much of this process the virus remains plentiful but nonetheless does not rekindle infection. Here, we analyze data from a set of individuals identified during acute HBV infection and develop mathematical models to test the role of immune responses in various stages of early HBV infection. Fitting the models to data we are able to separate the kinetics of the noncytolytic and the cytolytic immune responses, thus explaining the relative contribution of these two processes. We further show that we need to hypothesize that newly generated uninfected cells are refractory to productive infection. Without this assumption, viral resurgence is observed as uninfected cells are regenerated. Such protection, possibly mediated by cytokines, may also be important in resolving other acute viral infections.

Hepatitis B virus (HBV) is a small (≈3.2 kb) partially dsDNA virus that infects hepatocytes (1). There are >350 million chronic HBV carriers worldwide, and infection with HBV is the cause of significant morbidity and mortality in countries of high prevalence (2). During acute infection, HBV viral loads can reach high levels, up to 10¹⁰ HBV DNA copies per ml of plasma, which last for several weeks, coincident with HBV infection of a large percentage of hepatocytes (3–6). Subsequently, viral loads decrease, and in 85–95% of acutely infected adults the infection is cleared (7). Patients that clear the virus tend to have stronger and more diversified CD4⁺ and CD8⁺ T cell responses (8, 9). In addition, clearance of the virus in acutely infected patients is usually accompanied by an alanine aminotransferase (ALT) flare. Elevated levels of ALT are indicative of liver damage and an active cell-mediated immune response. Although the immune response plays a crucial role in decreasing the viral load, the precise mechanisms are not fully understood (10).

Studying the immune response to HBV during acute infection of humans is difficult, and the field has progressed by the study of experimental infection in chimpanzees, woodchucks, and ducks and transgenic mice that express HBV genes. These studies demonstrated the importance of the immune response, because acute infection in chimpanzees depleted of CD8⁺ T cells results in delayed HBV clearance and recovery (11). However, chimpanzee studies have also shown that the initial reduction in HBV viral load occurs much earlier than any detectable cytolytic immune response, liver T cell infiltration, or liver damage (3), suggesting that some form of noncytolytic response is involved. The importance of a noncytolytic response has been confirmed in the HBV transgenic mouse model, where type 1 and type 2 interferons inhibit the formation of HBV nucleocapsids and lead to HBV mRNA degradation (12–15). On the other hand, results from the woodchuck model have argued that clearance of covalently closed circular DNA (cccDNA) from the nucleus of infected hepatocytes proceeds through the death of infected cells and the regeneration of the liver with uninfected hepatocytes (16).

Thus, during the acute stages when clearance or chronic infection is decided, there is a subtle dynamic interplay between replenishment of uninfected cells and continuing rounds of viral infection. Indeed a fundamental question is how the new uninfected cells, generated by noncytolytic immune mechanisms and hepatocyte proliferation, do not rekindle the infection. It has been suggested that any surge in reinfection may be thwarted because of infected cells being replaced by cells that are protected from reinfection (17). Here, we introduce the idea of cells being refractory to reinfection or being resistant to viral replication as suggested earlier (18) in the context of heterogeneous differentiation states of hepatocytes. The mechanisms of resistance are unknown but it is reasonable to expect that the intracellular state set by the cytokine response persists for some period. Also, cells that are partially resistant to infection, say because of low levels of the receptors required for HBV infection, may selectively survive and expand during the many months of acute infection and contribute to a population of cells protected from infection. An effect of this type has been observed in cell-culture systems of HCV infection (19). Here, we explore the role of a class of cells refractory to productive infection in acute HBV infection.

Because of the difficulty of studying these issues experimentally, we introduce mathematical models of HBV dynamics to explore the mechanisms leading to viral clearance while maintaining liver integrity. We show that viral resurgence is expected to occur as new uninfected cells repopulate the liver unless these cells are resistant to infection while virus clearance occurs. We also suggest experimental tests of our hypothesis.

Results

Models of Acute HBV Infection.

To understand the important features of the immune response and virus dynamics during acute HBV infection, we modeled HBV DNA data from acutely infected patients (see Materials and Methods) by using different mechanistic models. We analyzed the effects of cytolytic vs. noncytolytic immune responses, the dynamics of target cell production, and the role of cells refractory to infection. As virus is cleared and infected cells are replaced by uninfected ones, our models highlight the need for mechanisms to prevent the infection of these newly generated cells.

We consider five populations, corresponding to uninfected hepatocytes (T), productively infected hepatocytes (T*), free virus (V), immune effector cells (E), presumably CD8⁺ T cells (14), and a population of refractory cells (R). This last population corresponds to either previously infected cells refractory to new infection, because of the continuing effects of a noncytolytic immune response, or a population of infected cells not producing measurable amounts of virus (see below). The dynamics of these populations are governed by the following differential equations:

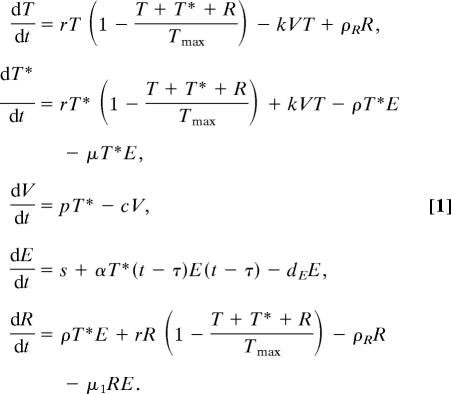We assume that in the absence of infection (V = 0, T* = 0, R = 0) the number of hepatocytes, T, is maintained by homeostasis described by a logistic equation, with carrying capacity T_max and maximal growth rate per hepatocyte r. Infection occurs with rate constant k. Physiologically, when hepatocytes are initially infected, they carry one copy of the genetic information of the virus in the form of a cccDNA genome. Additional copies of cccDNA accumulate in the cell through viral replication (20, 21). This accumulation may result in different HBV production rates by cells with different copy numbers of cccDNA (22). In the model, we simplify this aspect by considering only one class of infected cells, with multiple copies of cccDNA (T*), although in the supporting information (SI) Text we consider a model with more than one class of infected cells. Infected cells can be killed by the immune response at a rate of μE per cell and proliferate in a manner similar to the uninfected cells. Because cccDNA does not replicate upon cell division, when T* cells divide it is possible that they originate cells with no cccDNA (23). However, even the progeny of an infected cell that contains no cccDNA in its nucleus may still contain viral components, such as relaxed circular DNA and partially assembled virions in its cytoplasm. Thus, the direct transition from T* to T by division of T* has a very small chance of occurrence, and we neglect it. Division of infected cells occurs at a growth rate r.

One feature of our model is that infected cells can be lost because of the noncytolytic response, dependent on the effector cell population E, by recovery into a population of refractory cells (R), at a rate of ρE per cell. This phenomenon has been hinted at by experimental results (17). Because cell surface antigens characteristic of infected cells persist for some time (3), the refractory population may still be assayed as infected by antibody staining. However, we assume these cells do not produce virus (or produce negligible amounts), because they have lost most or all of the replicative intermediates and cccDNA (3, 22). This population divides at the same rate as uninfected hepatocytes. Eventually, these cells will move into the true uninfected population at a rate of ρ_R per cell.

Free virus is produced at rate p and virus is cleared from circulation by all mechanisms at rate c.

In the absence of infection we assume there is a basal level of specific immune effector cells E, given simply by s/d_E, where s corresponds to a source of effector cells with the specificity for HBV-infected cells and 1/d_E is their average lifespan. This basal level is meant to represent antigen-specific naive CD8⁺ T cells that upon encounter with antigen are activated, clonally expand, and differentiate into true effector cells. To account for the lag usually observed between infection and the immune response [observed in HBV infection (24) and other infections (25–29)], we allow for a time delay (τ) between antigen encounter and effector cell expansion.

Viral Dynamics.

We fitted our model to the data from seven HBV-infected individuals detected at the stage of acute infection (see Materials and Methods and Fig. 1) (24, 30, 31). The fits demonstrate a biphasic decay in the viral load for all patients. The median estimated duration of the first phase was 75 ± 25 days, and the duration of the second phase was 152 ± 35 days. In Tables 1 and 2, we present parameter estimates and 95% confidence intervals (C.I.), respectively, corresponding to the best fit of our model to the data for each patient (see Materials and Methods).

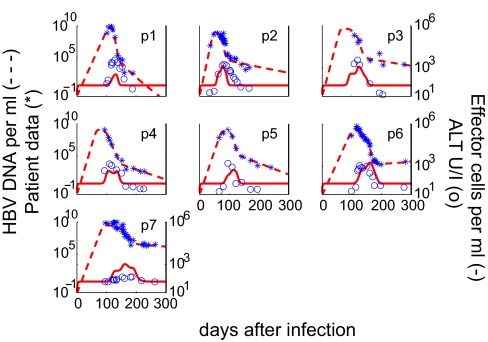
Fig. 1.

Results of fitting the model to each patient's HBV DNA data and the relationship between effector cells and serum ALT during the acute phase of the infection. The best fit of the model (dashed lines) to HBV DNA patient data (∗) is indicated. The measured serum ALT (○), which was not used in data fitting, compares well with the predicted dynamics of the HBV-specific effector cell response (solid lines).

Table 1.

The best-fit estimates of the parameters in the model given by Eq. 1

Patient	μ, day−1 × 10−4	μ1, day−1 × 10−6	α, day−1 × 10−7	τ, day	ρ, day−1 × 10−3	p, day−1	k, day−1 × 10−10
1	72	150	2.2	15.2	0.729	400	0.653
2	1.5	0.2	3.2	19.6	1.06	57	7.81
3	6.9	37	2.3	29.0	0.311	189	1.74
4	0.1	0.07	3.5	34.4	1.87	77	3.87
5	20	0.4	1.2	16.8	0.119	39	6.49
6	0.003	180	4.4	29.7	1.03	76	2.22
7	1.2	12.7	2.0	33.4	0.338	164	1.22
Geomean	1.28	5.0	2.5	24	0.566	107	2.49
GEO 95% C.I.	0.1–16.4	0.46–56	1.8–3.4	18.8–31.2	0.282–1.14	59–194	1.28–4.86

Table 2.

Bootstrap 95% C.I. for the parameter estimates

Patient	μ, day−1 × 10−4	μ1, day−1 × 10−6	α, day−1 × 10−7	τ, day	ρ, day−1 × 10−3	p, day−1	k, day−1 × 10−10
1	(71.9, 72.1)	—	(1.38, 3.81)	(14, 18)	(0.728, 0.731)	(387, 416)	(0.653, 0.655)
2	(0.0008, 19)	(0.004, 8.0)	(1.52, 3.56)	(15, 23)	(0.321, 1.6)	(27, 83)	(5.51, 16)
3	(6.7, 7.1)	(35, 38)	(1.99, 2.58)	—	(0.309, 0.312)	—	(1.74, 1.75)
4	(0.003, 12)	—	(1.95, 4.24)	(25, 47)	(0.43, 2.66)	(29, 164)	(2.16, 6.74)
5	(10, 28)	(0.07, 820)	(0.95, 2.17)	(14, 23)	(0.043, 1.18)	(25, 77)	(3.27, 9.35)
6	(0.0003, 20)	(0.2, 950)	(2.63, 6.06)	(25, 39)	(0.287, 2.1)	(47, 116)	(1.56, 3.54)
7	(1.19, 1.21)	(12.7, 12.8)	(1.74, 2.10)	(31, 37)	(0.337, 0.338)	(164, 165)	(1.22, 1.23)

The median fraction of productively infected cells at the peak of infection is 86% of total hepatocytes, varying from a minimum of 63% to a maximum of 96%. If the refractory cells are still hepatitis B core antigen (HBcAg)⁺ and thus counted as infected by standard immunological assays (3, 22), then virtually all hepatocytes are infected at the peak of infection (Fig. 2a), consistent with observations in primary infection of chimpanzees, where >75% of hepatocytes were HBcAg⁺ at the peak of viremia (3).

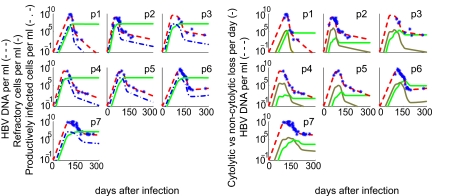
Fig. 2.

The predicted temporal relationship of the cytolytic and noncytolytic response to the level of infection and the HBV DNA viral load. Displayed for each patient are the measured HBV DNA (∗) and best-fit model predictions for: the HBV DNA viral load (dashed line), the number of refractory cells, R (solid line) and the productively infected cells, T* (dashed-dot line) (a); and noncytolytic immune response, ρT*(t)E(t)) (gold line), cytolytic immune response, μT∗(t)E(t)+μ₁R(t)E(t) (green line) (b). Note that the noncytolytic immune response occurs before the cytolytic response and peaks coincident with the viral load (red line).

Refractory Cells.

After the peak in viral load, the number of infected cells declines quickly. Some are lost by a cytolytic immune response but most are converted into refractory cells (Fig. 2a). These cells reach their maximum around the peak in viral load and stay elevated throughout the analysis period. They are crucial in preventing a rekindling of the viral infection and concomitant viral rebound. To demonstrate this behavior, we present in SI Text the results of two models without refractory cells. In one of them, we still have a noncytolytic response, but it gives rise to “cured” target cells (i.e., T* goes directly to T at rate ρ; SI Fig. 3); in the other model, there is no noncytolytic effect at all (i.e., ρ = 0; SI Fig. 4). Both of these alternative models explain the data very poorly and show a characteristic oscillation in the viral load, because of too many target cells being generated, which leads to a recrudescence of infection. The difference is that in the first model (SI Fig. 3) virus is reduced each time by a vigorous noncytolytic response. In SI Fig. 4, the reduction in virus at each cycle is caused by extensive depletion of hepatocytes (up to 90%) driven by the cytolytic immune response. Both scenarios, with viral oscillations and massive hepatocyte depletion, are not realistic. However, these models raise a very important biological question, namely, if viral load decline is accompanied by a decrease in infected cells, and a concomitant increase in uninfected cells, what prevents these cells from becoming targets for new infection, thus increasing viremia? Indeed, avoiding the increase in new targets for infection is the function of the R population in our model.

With the 300-day data that we have, it is difficult to assert the physiological fate of these refractory cells. Although in the model we observe a very slow loss of these cells to prevent rekindling of infection, it is likely that this loss could be faster, as the viral load declines and the immune mechanisms responsible for the refractory state (e.g., inflammation) subside and neutralizing antibody accumulates (see Discussion). Thus, these cells would more quickly revert to a nonrefractory state.

Effector Cell Dynamics.

To understand the mechanisms behind the viral decline, we studied the relationship between viral decay and the change in HBV-specific effector cells, E, in our model. The initial rapid and sharp fall in HBV DNA levels took place around the peak of the noncytolytic immune response, which occurred a median of 31 ± 11 days before the peak in the cytolytic response (Fig. 2b). We observed a median of 98% reduction in viral load from the peak before the cytolytic response reaches its maximum, supporting the argument made by Guidotti et al. (3), based on studies of the chimpanzee model, that the initial fall of HBV in blood and liver is caused by noncytolytic mechanisms.

The estimated median delay in HBV-specific effector cell activation, τ, is 29 ± 8 days, with the longest delays of ≈5 weeks occurring in patients 4 and 7. The maximum effector response occurred a median of 124 ± 29 days after infection, with a median of 415 ± 350 cells/ml.

The data show that patient 7, who was immunosuppressed because of a corticosteroid drug regimen (24), has the slowest second phase and a long incubation period. We conjecture that the data-consistent parameters found for this patient, revealing a weak cytotoxic killing, μ, low immune activation rate, α, and a long delay for effector cell activation, τ, may be responsible for the development of chronic infection in this case. Indeed, during the second phase of viral reduction, we observed a drop in HBV DNA of only 37-fold in patient 7, compared with a median 100-fold in the other patients. Also, our simulations show that the peak of the immune response in this patient occurs late, 23 weeks after infection, ≈5 weeks later than the median.

To better characterize the effector cell contribution to viral reduction, we analyzed alternative models for the immune response: no noncytolytic response (ρ = 0, as above) and no cytolytic response (μ = μ₁ = 0); see SI Text. In the first case (SI Fig. 4), infected cells are cleared only by cytolytic mechanisms and the model predicts an unrealistically large depletion of hepatocytes at the peak of infection (as detailed above). To avoid this depletion, we could assume a much faster production of uninfected cells by compensatory proliferation, but this always leads to viral rebound (SI Fig. 4 and data not shown). This rebound can only be avoided if the newly generated hepatocytes are somehow refractory to infection.

We then tried a model without a cytolytic immune responses (SI Fig. 5). The fits obtained were almost identical to those in the original model (Eq. 1). Comparing the sum of squared residuals of these two models shows no statistically significant difference between them (F test; P > 0.57). However, sustained noncytolytic responses involving high levels of cytokine secretion may cause self-damage (32), a feature not in our model, and thus this mechanism may be disfavored by the host. Nonetheless, given the model's consistency with the data, we also explored a model with just a noncytolytic response, but one that was independent from the effector cell dynamics. That is, the term ρET* in Eq. 1 became ρT* (SI Fig. 6). This model generates a monophasic viral decay. There is no statistically significant improvement in the sum of squared residuals in model 1 compared with this simpler model by an F test (P > 0.27). However, there are systematic errors with the theoretical curve either being above or below the data for long periods (e.g., see SI Fig. 6, patient 6). Further, the model predicts a simple monophasic viral decay from the peak, which is contradicted by the data (SI Fig. 6).

Finally, we considered the effects of removing both the cytolytic and noncytolytic responses by setting E to zero. This mimics experiments in which anti-CD8 mAbs were used to deplete the CD8⁺ T cells responsible for the cytolytic and noncytolytic immune responses in HBV-infected chimpanzees (11). The results (SI Fig. 7) show that the viral load reaches a set point at the peak of the infection and that clearance does not occur. This finding is similar to the experimental results in CD8-depleted chimpanzees (11).

Liver Disease.

To further demonstrate the relationship of the cytolytic immune response and hepatocyte death, we compare the clinically measured values of the liver enzyme ALT and the effector cell dynamics, E, predicted by our model (Fig. 1). The serum level of ALT is usually used as a surrogate marker for the degree of hepatocyte damage (33). Fig. 1 shows that there is a good correlation among the predicted timing of the cell-mediated immune response, E (solid line), and the measured ALT level (circles). We also compared the ALT levels with the rate of infected cell killing and show the initiation of cell killing correlates with the initiation of ALT elevation (SI Fig. 8). This correlation is also observed in the more complex model with more than one class of infected cells (SI Fig. 9). We emphasize that these correspondences are an independent confirmation of our model, because we did not use the ALT data in our analysis. This correspondence between the measured increase in ALT levels and our computed change in effector cell number suggests that the cytolytic effect of the immune response plays a role in reducing HBV viral load, albeit at a late stage. Moreover, these results are in agreement with the observed simultaneous rise in ALT and HBV-specific CD8⁺ T cells in two HLA-A+ patients (for which HBV-specific tetramers exist) (24).

Discussion

HBV has a long incubation period (8–20 weeks), reaching a peak of up to 10¹⁰ copies/ml ≈10–12 weeks postinfection (34). After the peak, the viral load decreases in a biphasic manner (Fig. 1). As the viral load decreases and the infection resolves, infected cells are replaced by uninfected ones. A fundamental question that has not been adequately addressed is what prevents these newly generated uninfected cells from being infected. The immune response is clearly important, and both cytolytic and noncytolytic mechanisms of HBV-specific CD8⁺ T cell activity have been observed (10, 35). Cytolytic mechanisms only remove cells once they are infected and hence cannot prevent the infection of cells. Noncytolytic mechanisms can influence viral replication and the stability of viral replicative intermediates. Here, we have postulated that such noncytolytic mechanisms induce an “antiviral state” in which newly generated uninfected cells are refractory to further infection. To test this idea and gain insight into the events that underlie the early kinetics of HBV infection, we developed a mathematical model and fitted it to data from seven patients identified early in infection.

The model was consistent with the viral load data (Fig. 1) and many other observations in both human infection and animal models of HBV infection. First, the results of our model suggested that noncytopathic mechanisms are important early in infection while the cytolytic response plays a role late in infection (Fig. 2b), as has been shown for acute HBV infection in the chimpanzee (3, 22). Further, our results are in agreement with the effects of depletion of CD8⁺ T cells in the chimpanzee model of primary HBV infection. Such depletion prevents clearance of the virus in the chimpanzee (11) and in our model (SI Fig. 7). The model also predicts that elevation in effector cell levels occurs very close to the experimental peak in ALT level (even though information about ALT was not used to fit the HBV DNA data).

We calculate that cumulatively up to 375% of hepatocytes were regenerated during the 300 days after infection, presumably to compensate for killing of infected cells. This finding is consistent with recent studies in the woodchuck model of transient hepatitis indicating a turnover of 100–200% of the total hepatocyte population, during the resolution of infection (16, 17). Also, it was recently estimated that turnover of hepatocytes in the resolution of primary infection, in two chimpanzees, results in more than two full livers being regenerated (22). Even though we calculate a large amount of cell death, the total number of hepatocytes is maintained approximately constant by homeostasis, suggesting a crucial role for hepatocyte proliferation in regulating liver integrity. The liver has an important regenerative capacity (36), and in chimpanzees during resolution of HBV infection (around the peak in ALT) up to 40% of hepatocytes express proliferating cell nuclear antigen (37).

As the liver is regenerated, the newly produced hepatocytes could become targets for the virus, rekindling the infection. Thus, to clear virus, these new hepatocytes should not serve as targets for infection (4, 17). We hypothesized this protection is accomplished by the existence of a state refractory to productive infection. We note that these cells may be similar to the refractory cells defined by the model in refs. 38 and 39, in the sense that they are resistant to viral replication and less susceptible to induced cell death. This refractory state has been hinted at by experimental results (17), and it is crucial in our model to explain the viral load profiles seen in the data.

We also considered the possibility that neutralizing antibody (antihepatitis B surface antigen) could prevent hepatocyte infection (40). Such a model without R cells could not fit the data (data not shown), in part because the overwhelming excess of surface antigen positive viral particles without DNA (1) absorbs most of the antibody produced during primary infection. Nonetheless, neutralizing antibody could play a role late when virus and subgenomic particles are largely cleared. Further, as noncytolytic immune responses shut off because of a lack of antigen stimulation, cytokine secretion will be curtailed and refractory cells might lose their antiviral state. At this point, neutralizing antibody could continue to prevent rekindling of the infection from any remaining infectious virus. Future models will be needed to examine this idea in detail.

Another important issue is the nature of the refractory population, R. As the number of infected cells declines, whatever the mechanism (cytolytic vs. noncytolytic), one expects that many new target cells are generated, with the potential for new infections and renewed viral production. In our model, R cells cannot produce virus and thus are crucial in reducing the viral load. The cells are assumed to remain targets for a cytolytic response and hepatitis B surface antigen probably persists. Whether such cells would also be HBcAg⁺, and hence detected by antibody staining as infected, remains to be determined. Further, it is unclear whether R cells are a phenotypically defined population. Rather they could correspond, for instance, to a fraction of cells protected from infection by cytokines (17), or cells in an internal state of low tolerance for infection (41), or even cells that produce virus at extremely low rates. They also might be cells that express low levels of the yet-unidentified receptor needed for viral entry.

Although our model is consistent with existent data, it is important to see whether it can be disproved. Cell culture systems for HBV have been developed and have been used to show that lymphocytes from patients with chronic HBV infection can inhibit viral replication in human hepatocytes by releasing IFN-γ (42). However, the inhibition of viral replication was not complete (42), and thus factors other than IFN-γ may be mediating the effects we have postulated. Nonetheless, similar technology could be exploited to test our hypothesis. If hepatocytes from diagnostic liver biopsies could be obtained from acutely infected patients both before and well after the viral peak, they could be put in culture with patient viral isolates or serum obtained early in infection to minimize the possibility of neutralizing antibody being complexed with the patient's virus. Our model predicts that viral replication would be better supported in the early biopsy culture than in the later one, which we predict should contain refractory cells. If human isolates were not available, the comparable experiment could be done in animal models.

Another significant experiment would be to determine in vivo the turnover of hepatocytes during primary infection. The know-how to make these measurements already exists (for instance by using BrdU or deuterated glucose) (43), but doing them in humans, which involves serial biopsies, is probably not feasible. Still, the animal models used to study other aspects of HBV infection would be suitable to verify the amount of proliferation, as well as the timing, which should be simultaneous with the cytolytic response (increases in ALT) and somewhat later than the initial decay of viral load, as predicted by our model.

In summary, we have developed a model of acute HBV infection that gives a clear picture of the early events in the immune response against acute HBV infection. In particular, it shows that an important process in HBV control and potential clearance may be the appearance of a population of cells refractory to infection or in which viral production is inhibited. Determining whether such cells exist and elucidating their nature remains an important problem in HBV infection and may give insights into the mechanisms involved in clearing other viral infections. The issue we raise of how recrudescence of infection is prevented, as uninfected cells replace infected ones, during clearance of acute infection by cell-mediated immune responses is a general one. Its resolution may inform us of the possibility of success of new vaccines that aim to stimulate cell-mediated responses rather than antibody responses.

Materials and Methods

Patient Sources.

In 1998, seven patients were identified in the acute stage of infection during a single-source HBV outbreak (24, 30). They were all infected with the same HBV variant and were anti-hepatitis C virus and hepatitis delta virus antibody negative (24, 30). In patients 1 and 6, identified in the incubation period, the time of infection relative to the viral peak was estimated to be 117 and 120 days, from analysis of the doubling time of the virus before the peak (31). In the case of patient 2 this time was known to be 80 days (31). For the other patients the time of infection was uncertain, and we assumed the mean time between infection and the viral load peak to be 100 days.

The data we analyze consist of longitudinal measurements of HBV DNA per ml of blood for these seven patients during the first 8–10 months of infection. Between 7 and 29 measurements were made per patient, on average every 12 days. Initially, viral load increased exponentially, reaching a peak of up to 10¹⁰ HBV DNA copies per ml, then it declined in a biphasic manner, and appeared to approach a plateau ≈6 months postinfection. However, from the epidemiological data we know that patients 1–6 cleared the infection at some later time, whereas patient 7 developed chronic HBV infection (24, 30) and died shortly thereafter from fibrosis lung disease.

Parameter Estimation.

After injury the liver can rapidly regenerate. We assume during infection that the maximum proliferation rate for both uninfected and infected hepatocytes is r = 1 per day (44), corresponding to approximately a division every 16 h. The total number of hepatocytes in the liver, T_max, has been estimated at ≈2 × 10¹¹ (45). Because the available data pertains to HBV per ml of serum and we assume HBV DNA can distribute throughout the 15 liters of extracellular fluid in the average 70-kg person, we normalize the liver cell population so that we consider the cells responsible for producing virus in 1 ml. Hence, we take T_max = 13.6 × 10⁶ cells/ml. Webster et al. (24), using MHC peptide tetramers in three HLA-A2⁺ patients, assayed for HBV-specific CD8⁺ T cells (E) with a limit of detection ≈0.02% of total CD8⁺ T cells. We assume that before infection we have an undetectable number (0.02%), that is 60 cells per ml, assuming a total of 300 CD8⁺ T cells per μl in a typical patient (24). Effector cells are short-lived and we assume a death rate d_E of 0.5 per day (46), so that s is determined by the preinfection steady state, i.e., s = 30 cells per day. We also use the estimates from earlier studies for the viral clearance rate, c = 0.67 day⁻¹ (47, 48). As in Whalley et al. (31), we consider the amount of HBV-contaminated blood that initiated infection in this outbreak to be small, i.e., 10³ HBV virions. Because this inoculum was injected directly into the blood we assume (as in ref. 31) that the HBV DNA is diluted in 3 liters of serum, rather than the 15 liters of extracellular fluid, which gives an initial concentration of 0.33 virus per ml. Lastly, to prevent viral resurgence refractory cells cannot convert rapidly to target cells. We, thus, set ρ_R = 2 × 10⁻⁵ day⁻¹, a value found by a Monte Carlo search algorithm to be consistent with the viral load data. In our analysis, we keep all these parameters fixed.

We estimated the remaining parameters, α, μ, μ₁, τ, ρ, p, and k, by fitting the model to the measured viral load data using a nonlinear least-square regression method based on a hill climbing Monte Carlo algorithm (see ref. 25 and SI Text) to find initial parameter guesses. These were used as starting values in a Levenberg-Marquardt algorithm to find the best fit parameters (49). To calculate the 95% C.I. of these estimated parameters, we used a method based on bootstrap sampling of the residuals (see ref. 50 and SI Text). In four cases (see Table 2), the bootstrap for the C.I. did not converge, thus we could not calculate C.I. for all parameters in those cases. We opted to fix one or more parameters at its estimated value and calculated the C.I. for the other parameters. As shown in Table 1, for some parameters, there was large interpatient variation in the best-fit value. Moreover, because parameter values were constrained to be positive, their distributions were skewed to the right. For these reasons, we computed the geometric mean and the geometric 95% C.I. rather than their arithmetic analogues.

Abbreviations

ALT

alanine aminotransferase

cccDNA

covalently closed circular DNA

C.I.

confidence interval

HBV, hepatitis B virus, HBcAg

hepatitis B core antigen.