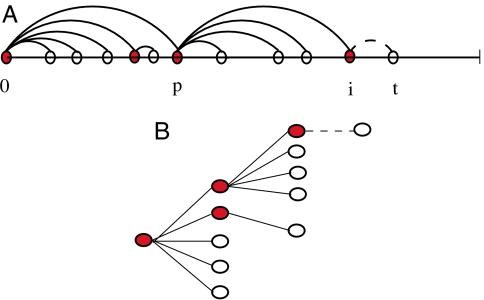
Fig. 1.

The one-parameter TPA model. (A) An example of the growth process on the line, with 1/α = 4. Node t arrives and wants to minimize the cost function αn_tj + h_j, where n_tj is the number of existing nodes in the interval between t and j, and h_j is the hop-count of node j to the root. The minimization can only be achieved by connecting to the adjacent node i (so that n_ti = 0), or to the parent of i (which has h_p = h_i − 1). If n_tp ≥ 1/α (as is the case illustrated), i gains the new attachment, otherwise p does. Thus as soon as there are 1/α children of node p, node p's attractiveness saturates. (B) The equivalent network structure resulting from the growth process on the line.