Fig. 2.

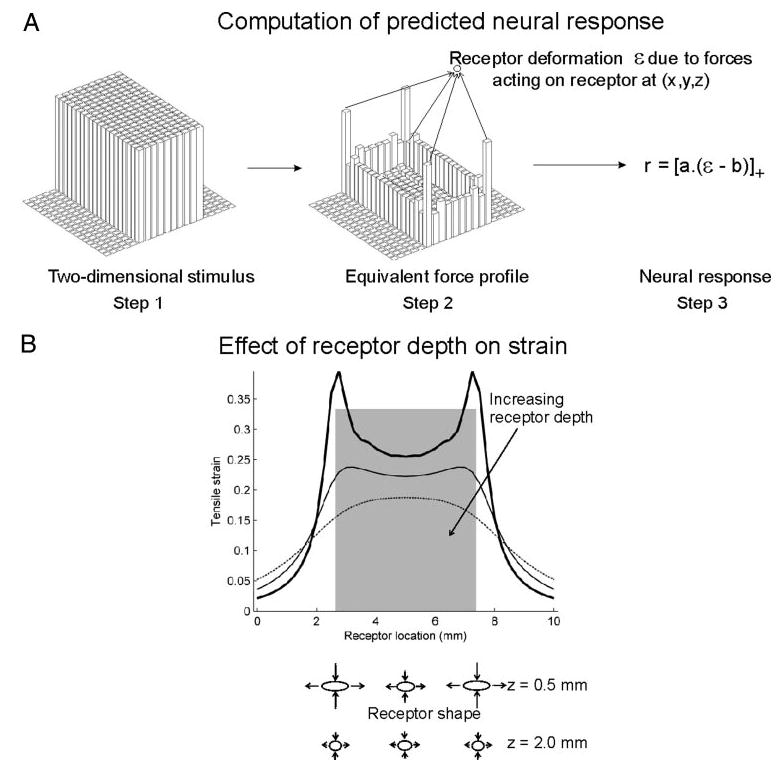
A: schematic description of the computation of the neural response using the continuum mechanical model. First, a 2-dimensional stimulus (here, an indented bar) is redefined in terms of the forces required to produce this pattern of indentations (step 1). Next, this equivalent force profile is used to compute the stress/strain variable ε at a point receptor located at (x,y,z) within the skin (step 2; positive z values indicate depths below the resting skin surface). Finally, the stress/strain variable ε is scaled linearly and rectified to obtain the predicted neural response (step 3). The scalars a and b represent the afferent’s sensitivity and threshold, respectively. B: maximum tensile strain experienced along the cross-section of an indented bar (shaded region) by an array of receptors at 3 depths: 0.5 mm (thick line), 1 mm (thin line) and 2 mm (dotted line). If a spherical receptor is deformed into an ellipsoid, the length along the major (minor) axis is linearly related to the maximum tensile (compressive) strain; this is schematically shown under the abscissa for depths z = 0.5 and z = 2 mm. Edge enhancement (e.g., at z = 0.5 mm) occurs in the responses of SA1 but not RA afferents (see also Fig. 10).