Force Unfolding Kinetics of RNA using Optical Tweezers. II. Modeling Experiments

Abstract

By exerting mechanical force, it is possible to unfold/refold RNA molecules one at a time. In a small range of forces, an RNA molecule can hop between the folded and the unfolded state with force-dependent kinetic rates. Here, we introduce a mesoscopic model to analyze the hopping kinetics of RNA hairpins in an optical tweezers setup. The model includes different elements of the experimental setup (beads, handles, and RNA sequence) and limitations of the instrument (time lag of the force-feedback mechanism and finite bandwidth of data acquisition). We investigated the influence of the instrument on the measured hopping rates. Results from the model are in good agreement with the experiments reported in the companion article. The comparison between theory and experiments allowed us to infer the values of the intrinsic molecular rates of the RNA hairpin alone and to search for the optimal experimental conditions to do the measurements. We conclude that the longest handles and softest traps that allow detection of the folding/unfolding signal (handles ∼5–10 Kbp and traps ∼0.03 pN/nm) represent the best conditions to obtain the intrinsic molecular rates. The methodology and rationale presented here can be applied to other experimental setups and other molecules.

INTRODUCTION

Recently developed single-molecule techniques (1,2) have been used to exert force on individual molecules, such as nucleic acids (3–7) and proteins (8–10). These techniques make it possible to test the mechanical response of biomolecules that can be used to obtain information about their structure and stability. Moreover, the study of the kinetics, pathways, and mechanisms of biochemical reactions is particularly suited to single-molecule methods where individual molecular trajectories can be followed (11–13).

Optical tweezers have been used to study folding/unfolding (F-U) of RNA hairpins (14–17). The experimental setup consists of the RNA molecule flanked by double-stranded DNA/RNA handles; the entire molecule is tethered between two polystyrene beads via affinity interactions. The handles are polymer spacers required to screen interactions between the RNA molecule and the beads and to prevent direct contact of the beads. One of the beads is held in the optical trap; the other bead is controlled by a piezoelectric actuator to apply mechanical force to the ends of the RNA molecule. In hopping experiments, a given constraint, i.e., a fixed force or a fixed extension, is applied to the experimental system while both the force and the extension of the molecule are monitored as a function of time. Close to the transition force (∼10–20 pN for RNA or DNA hairpins at room temperature (13,14)), a hairpin molecule can transit between the folded (F) and the unfolded (U) states, as indicated by the change in the molecular extension: the longer extension represents the unfolded single-stranded conformation, the shorter one, the folded hairpin. From the lifetimes of the single RNA molecule in each of the two states, we can obtain the rates of the F-U reaction (1,14). Both the unfolding and folding rate constants are force-dependent following the Kramers-Bell theory (17–19). From their ratio, the force-dependent equilibrium constant for the F-U reaction can be obtained.

To obtain accurate information about the molecule under study it is important to understand the influence of the experimental setup, including the handles and the trapped bead, on the measurements. In a recent simulation, Hyeon and Thirumalai (20) examined the relationship between the amplitude of the F-U transition signal and the magnitude of its fluctuations at various handle lengths. On the other hand, experimental results have shown that the F-U kinetics was dependent on the trap stiffness (21). Questions then arise:

• How different is the measured rate from the intrinsic molecular rate, i.e., the F-U rate of the RNA in the absence of handles and beads?

• What are the optimal working conditions to obtain the intrinsic molecular rates?

To address such questions, we previously proposed a model (22), which considered the effect of the trapped bead and the handles on a two-state RNA folding mechanism. In this work, we further advance our simulation by incorporating a mesoscopic model introduced by Cocco et al. (23) that takes into account the sequence-dependent folding energy. We have then applied this model to a simple hairpin, P5ab (14). We investigate how the measured rates vary with the characteristics of the experimental setup and how much they differ from the intrinsic molecular rates of the individual RNA molecule. In a companion article, we have also measured the F-U kinetics of the RNA hairpin by optical tweezers (1). The theoretical and experimental results agree well.

The organization of the article is as follows. First, we introduce the model for the experimental setup and describe its thermodynamic properties. We also analyze the characteristic timescales of the system. Next, we discuss the influence of the different elements of the experimental setup on the kinetic rates. Limitations of the instrument that affect the measured F-U rates, such as the force-feedback time lag and the data acquisition bandwidth, are also considered. Based on the various timescales of the different dynamical processes characteristic of the experimental system, we develop a kinetic model for the RNA hairpin and a numerical algorithm used to simulate the hopping dynamics. Then, we carry out a detailed analysis of the dependence of the kinetic rates on the characteristics of the experiment (such as the length of the handles and the stiffness of the trap), and compare our simulation results with the experimentally measured F-U rates. A search of the best fit between theory and experiments allows us to predict the value of the intrinsic molecular F-U rate of the RNA molecule. Finally, we discuss the optimal experimental conditions needed to minimize the effect of the instrument and obtain the intrinsic molecular rates.

EXPERIMENTAL SETUP AND EXPERIMENTAL MODES

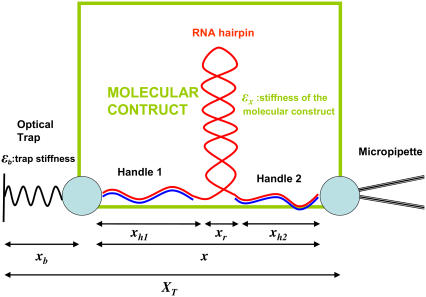
Hopping experiments (1) were done with a single RNA hairpin P5ab, a derivative of the L-21 Tetrahymena ribozyme. The kinetics of this RNA with 1.1 Kbp handles had been studied previously (14). In Fig. 1, we show a schematic picture of the setup used in such experiments. To manipulate the RNA molecule two RNA/DNA hybrid handles are attached to its 5′- and 3′-ends. The free ends of the handles are attached to micron-sized polystyrene beads. One bead is held fixed in the tip of a micropipette while the other bead is trapped in the focus of the laser, which is well described by a harmonic potential of stiffness ɛ_b. 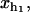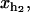The configurational variables of the system x_b, i.e., x_r, and are the extensions of each element (trapped bead, RNA molecule, and handles, respectively) along the reaction coordinate axis (i.e., the axis along which the force is applied). The external control parameter X_T is the distance between the center of the optical trap and the tip of the micropipette. In an experiment, the applied force f and the distance x_b are measured. From the value of x_b the changes in the distance between the two beads x, corresponding to the end-to-end distance of the molecular construct formed by the two handles and the RNA molecule (Fig. 1), can be obtained; x = X_T − x_b − R_b1 − R_b2, where R_b1 and R_b2 are the radii of the beads. A more detailed description of the experimental setup is given in Wen et al. (1).

FIGURE 1.

Schematic picture of the model for the experimental setup used in the manipulation of RNA molecules. We show the configurational variables of the system x_b, i.e., x_r, x_h1, and x_h2, which are the extensions of each element (trapped bead, RNA molecule, and handles, respectively) along the reaction coordinate axis (i.e., the axis along which the force is applied). X_T is the end-to-end distance of the whole system, i.e., the distance between the center of the optical trap and the tip of the micropipette. The optical potential is well described by a harmonic potential of a one-dimensional spring of stiffness ɛ_b and equilibrium position at x_b = 0.

In hopping experiments, the force f and the changes in the extension x as a function of time are recorded. The structural changes of the RNA molecule can be identified with the sudden changes in force and extension, here referred to as Δf and Δx, respectively. Experiments are carried out in two different modes: the passive and constant-force modes. In the passive mode (PM), the distance X_T between the center of the trap and the tip of the micropipette is held fixed. In PM hopping experiments both the extension x and the force f hop when the molecule switches from one state (F or U) to the other. In the constant-force mode (CFM), the force is maintained constant by implementing a force-feedback mechanism. In CFM hopping experiments the changes in the state of the RNA molecule can be identified with the measured changes in the extension x of the molecular construct. Experimentally, P5ab folds and unfolds with no apparent intermediates (1,14). The experimental traces show jumps in force and extension, Δf and Δx, which correspond to the full unfolding or folding of the RNA hairpin. From the data, we can extract the mean lifetimes of the F and the U states of the molecule, τ_F and τ_U, at a given force. The folding and unfolding rates, k_F and k_U, are the reciprocal of τ_U and τ_F, respectively.

Thermodynamics of the experimental system

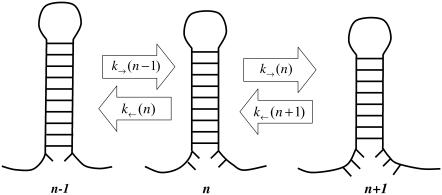
The experimental setup is modeled as previously described (22). The bead confined in the optical trap is considered as a bead attached to a spring whose stiffness equals the trap stiffness, ɛ_b, and the double-stranded DNA/RNA handles are modeled by the wormlike chain (WLC) theory (24,25), which describes the elastic behavior of polymers by two characteristic parameters: the contour (L) and the persistence (P) length. In our previous model (22), we considered a two-state model for the F-U of an RNA molecule. Here we extend that approach by including intermediate configurations of the hairpin where a partial number of basepairs (bps) are opened sequentially starting from the end of the helix. In this description, the molecule can only occupy intermediate configurations in which the first n bps are unpaired and the last N–n are paired, where N is the total number of bps in the native hairpin. The index n is used to denote such intermediate configurations (Fig. 2), e.g., the F state corresponds to n = 0 and the U state to n = N. This representation excludes the existence of other nonsequential breathing intermediate configurations that might be relevant for thermal denaturation (26). For a given value of the control parameter (generically denoted by y, e.g., X_T or f), and for each configuration n of the RNA molecule, we can define the thermodynamic potential G(y,n) as (22)

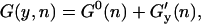(1)

where G⁰(n) is the free energy of the RNA hairpin at the configuration n and G′_y(n) describes the energetic dependence of the experimental system on the control parameter. Note that the term G′_y(n) is sequence-independent, so all information about the sequence is included in the term G⁰(n). The critical control parameter (F^c or 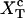) is the value of the control parameter at which the F and U states are equally populated. For the P5ab hairpin, the value of the critical force measured in the experiments is ∼14.5 pN (1).

FIGURE 2.

Schematic representation of the kinetic model for the RNA hairpin. The model assumes that the dynamics of the folding and unfolding of the hairpin is sequential. Therefore, each intermediate configuration n is only connected to its first neighbors n+1 and n−1, where n represents the number of sequential bps unpaired from the opening of the helix. The kinetic rates to go from n to n−1 or n+1 govern the F-U dynamical process.

In the ideal-force ensemble (hereafter referred as IFE), the force exerted upon an RNA hairpin is the control parameter (y = f) and the system reduces to the naked RNA molecule without beads and handles. The contribution G′ to the free energy of the RNA molecule is given by (27)

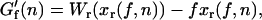(2)

where W_r(z) is the work required to stretch the molecular extension x_r of the ssRNA from x_r = 0 to x_r = z. In our experiments (Fig. 1), where handles, beads, and the RNA molecule are linked, the natural control parameter in Eq. 1 is y = X_T. This defines what has been denoted as the mixed ensemble (hereafter referred as ME) (28). In such case the contribution G′ in Eq. 1 has been derived in (22)

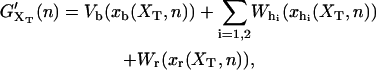(3)

where x_α(X_T,n), with α = b,h₁,h₂,r, is the mean value of x_α for a given value of the control parameter X_T and for a given configuration n of the RNA hairpin. V_b represents the optical trap potential, 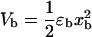and W_α(z), with α = h₁,h₂,r, is the work done upon each of the handles and the ssRNA to stretch their molecular extensions from x_α = 0 to x_α = z,

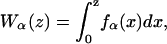(4)

where f_α(x) is the equilibrium force extension curve for the element α (22). These different contributions to the thermodynamic potential are free energies corresponding to the trapped bead, the handles, and the ssRNA molecule. Therefore, in the ME, the thermodynamic potential given by Eq. 1 depends not only on the RNA properties but also on the characteristics of the different elements of the setup, such as the stiffness of the trap and the contour and persistence lengths of the handles. To extract thermodynamic information of the RNA molecule from the experimental results, we need to take into account the contribution from each of the elements forming the setup (22). In the Supplementary Materials we show how the shape of the thermodynamic potential (Eq. 1) is modified for different values of the stiffness of the trap and the length of the handles. The characteristics of the experimental setup change the value of the maximum of the free energy along the reaction coordinate, which is related to the kinetic barrier separating the F and U states, and thus influences the kinetics of the F-U reaction. The dependence of the F-U rates of a DNA hairpin on the stiffness of the trap has already been reported (21).

In particular, when the experimental system gets softer, the fluctuations in force decrease and the ME approaches the IFE. The free energy landscape 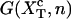converges to 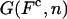corresponding to the IFE, in the limit where the effective stiffness ɛ_eff of the whole experimental system vanishes. The effective stiffness ɛ_eff is computed as

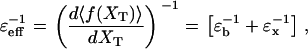(5)

where ɛ_b is the stiffness of the trap and ɛ_x is the rigidity of the molecular construct (i.e., the molecule of interest plus handles, see Fig. 1). Therefore, the thermodynamics of systems with longer handles (i.e., softer handles) and softer traps approaches the IFE case, as shown in Fig. S1 in the Supplementary Materials. However, thermodynamics alone is not sufficient to enable us to understand the influence of the experimental setup on the kinetics. For this, we have to consider a kinetic description of the system. This is the subject of the next sections.

Timescales in the system

The dynamics of the global system presented in Fig. 1 involves processes occurring at different timescales. Therefore, to study the kinetics, it is essential to analyze the different characteristic times of the system: the relaxation time of the bead in the trap τ_b; the relaxation time associated with the elastic longitudinal modes for the handles and the ssRNA, denoted by τ_handles and τ_ssRNA, respectively; the time 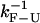in which the RNA hairpin folds and unfolds; and the basepair (bp) breathing time 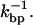Table 1 reviews the different characteristic times of the experimental system.

TABLE 1.

Different characteristic timescales of the system shown in Fig. 1

τb [ms]	τhandles [ms]	τSSRNA 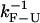[ms]	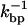[ms]	[ms]	B−1 [ms]	Tlag [ms]
1–10−2	10−3–10−5	3.5×10−6	104–10	10−3–10−5	102–1	102

Relaxation time of the bead in the trap is τ_b; the relaxation time associated to the longitudinal modes of the handles and the ssRNA is denoted by τ_handles and τ_SSRNA, respectively; the RNA hairpin folding-unfolding time is 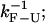bp breathing time is 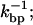and for intrinsic times of the instrument, average sampling time is B⁻¹, and time lag of force feedback mechanism is T_lag.

Bead

The time at which the bead in the optical trap relaxes to its equilibrium position is given by (22)

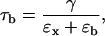(6)

where γ (γ = 6πR_b1η, where η is the viscosity of water) is the frictional coefficient of the bead, and ɛ_b and ɛ_x are the stiffness of the trap and the molecular construct, respectively. Typical experimental values are ɛ_b ≈ 0.02–0.15 pN/nm for the trap stiffness; R_b1 ≈ 0.5–1.5 μm for the bead radius; and L_h ≈ 130–1300 nm and P_h ≈ 10–20 nm for the contour and persistence lengths of the handles, respectively, which result in values for the stiffness of the molecular construct of ɛ_x ≈ 0.15–1.5 pN/nm (computed by using the WLC (24,25) theory at forces at ∼15 pN). For these values, τ_b lies in the range 10⁻⁵–10⁻³ s. The corner frequency of a tethered bead is defined as the reciprocal of τ_b. Events that occur at frequencies higher than the corner frequency of the bead cannot be followed by the instrument.

Handles and ssRNA

The relaxation time associated with the longitudinal modes of the handles and ssRNA when a given force f is applied to their ends can be estimated from polymer theory (29) as

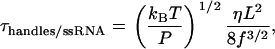(7)

where η is the viscosity of the water, (η ≈ 10⁻⁹ pNs/nm²); P is the persistence length of the double-stranded or single-stranded nucleic acids, respectively; T is the temperature of the bath; and k_B is the Boltzmann constant. For the handles used in the experiments (P_handles = 10–20 nm), the relaxation time lies in the range 10⁻⁸–10⁻⁶ s. For the ssRNA corresponding to the unfolded P5ab hairpin (N_ssRNA = 49 bases), τ_ssRNA is ∼3.5 × 10⁻⁹ s.

RNA molecule

There are two different timescales associated with the kinetics of the RNA molecule. The first timescale is the overall kinetic rate k_F-U given by

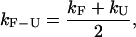(8)

where k_F and k_U are the folding and unfolding rates. The rate k_F-U depends on the sequence and structural features. Under tension at which a hairpin hops, typical values of k_F-U are in the range 0.1–100 Hz. The second timescale corresponds to the characteristic frequency for the opening/closing of single bps, 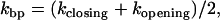which is estimated to be ∼10⁶–10⁹ Hz (30,31).

In summary, the dynamics of the system presents the following hierarchy of timescales

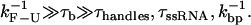(9)

A part from the timescales associated with each of the different elements in the system there are also intrinsic characteristic timescales of the instrument. It is important to consider them to understand and correctly analyze the results obtained from the experiments.

Instrumental times

Three characteristic timescales limit the performance of the instrument. The first timescale is defined by the bandwidth B, the rate at which data are collected in the experiments. Collected data represent an average of the instantaneous data measured over a given time window of duration 1/B. Typical values for the bandwidth used in the experiments lie in the range from 10 to 1000 Hz. The second important characteristic timescale is given by the time lag of the feedback mechanism, T_lag, implemented in the CFM. In our experiments (1), typical values for T_lag are 100 ms. To approach the IFE one would like T_lag as small as possible. Recently, a new dumbbell dual-trap optical tweezers instrument has been developed (21,32). This design operates without feedback and can maintain the force nearly constant over distances of ∼50 nm. Nevertheless, regardless of the specific instrumental design, there is a limitation in the measurement that is imposed by the corner frequency of the bead: the bead does not respond to force changes that occur faster than τ_b. In our experimental setup this limiting time is ∼10⁻⁴ s. The third timescale ranges from seconds to minutes and corresponds to the drift of the instrument. The drift is a low frequency noise due to mechanical and acoustic vibrations, air currents, thermal expansion in response to temperature changes, and other causes. Since the drift does not affect the occurrence and detection of F-U transitions, we did not take into account drift effects in our model.

MOLECULAR AND MEASURED RATES: INSTRUMENTAL EFFECTS

From the force and extension traces recorded in hopping experiments (1), we can extract the rates of the F-U reaction. These traces reflect the response of the whole experimental system (Fig. 1), not just the individual RNA molecule. In addition, data collected are averaged over a bandwidth B, and the mechanism implemented in the CFM has a finite response time, T_lag. In this section, we analyze the effect of the experimental setup on the measured F-U rates as compared to the intrinsic molecular rates.

Definition of the rates

There are different experimental modes and different ways of analyzing the experimental data that result in different values of the rates of the reaction; ultimately, we wish to obtain values as close as possible to the intrinsic molecular rates. The intrinsic molecular rate, 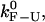corresponds to the rate measured in an IFE where a fixed force F^c (i.e., the critical force value where the F and U states are equally populated) is applied directly to the RNA molecule. In the following paragraphs, we introduce the different rates that are experimentally measurable, i.e., under the CFM and PM. These rates have been defined in our companion article (see (1) for details).

CFM rates

The CFM rates are the folding and unfolding rates measured when the instrument operates in the CFM at a given force. In what follows we will consider the critical rate 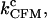which is the F-U rate (Eq. 8) measured at the critical force value where the molecule spends the same amount of time in the F and U states.

PM rates

The force traces in the PM show that the folding and unfolding transitions occur at different forces, f^F and f^U, respectively (see Fig. 4). The values f ^F and f ^U are the mean forces in the upper and lower bounds of the square-like force traces, respectively. The PM unfolding (folding) rate at f^F (f^U) is then identified with the unfolding (folding) rate measured in such PM traces from the lifetime of the folded and the unfolded states, respectively. The PM critical rate 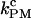is the F-U rate at the force value where the unfolding and folding PM rates are equal (see Fig. 6).

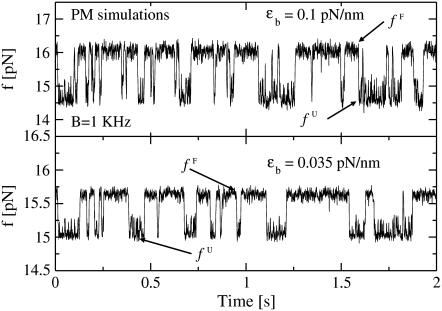
FIGURE 4.

Force traces for P5ab hairpin with 3.2 Kbp handles in PM from the simulations for two different trap stiffnesses ɛ_b ≈ 0.1 pN/nm (upper panel) and ɛ_b ≈ 0.035 pN/nm (lower panel). The bandwidth used is 1 KHz. We show the mean forces, f^F and f^U, in the upper and lower parts of the square-like-sign force traces, corresponding to the forces at the folded and unfolded states, respectively. Note that the value of such forces, f^F and f^U, is higher than the ones measured in experiments (1) by ∼1–1.5 pN. This discrepancy is consistent with the fact that the free energy parameters for P5ab used in simulations (32–34) corresponds to higher salt concentrations than the experimental ones.

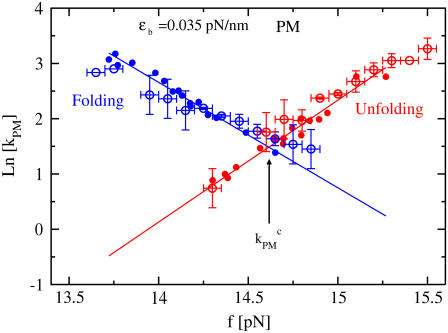
FIGURE 6.

The logarithm of the PM folding (in blue) and unfolding (in red) rates as a function of force from experiments (open circles) and simulations (solid circles). The folding and unfolding lines from simulations have been shifted by 1.5 pN to account for the experimental salt conditions. Straight lines are the linear fits to the data from the simulation. The intersection point between the folding and unfolding lines gives the value of the PM critical rate.

Instrumental effects

To study the relation between the measured and intrinsic molecular rates, we now consider the different effects that influence the kinetics in the CFM and PM as compared with the IFE. Under the experimental conditions, the force exerted directly on the RNA molecule (f_RNA) is subject to fluctuations due to the dynamic evolution of the different elements in the experiment (Fig. 1). There are at least three contributions to these fluctuations, as described below.

Bead-force fluctuations

On timescales on the order of τ_b, the force exerted upon the molecule fluctuates (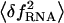) due to the fluctuations in the position of the bead (),

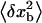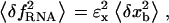(10)

where ɛ_x is the stiffness of the molecular construct. As shown in the Supplementary Materials, the effect of the fluctuations given in Eq. 10 is to increase the kinetics of the F-U reaction as compared with the IFE.

Basepair hopping effect

At the timescale at which bps attempt to open and close, 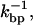the bead hardly moves (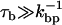). Hence, when a bp forms (dissociates), the handles and the ssRNA stretch (contract), and correspondingly there is an increase (decrease) in the force exerted upon the RNA molecule, f_RNA. The change in the force f_RNA after a bp opens or closes, assuming that in the timescale 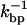the position of the bead is fixed, is given by

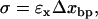(11)

where Δx_bp is the difference in extension between the formed and dissociated bp. Therefore, after the formation (rupture) of a new bp, the force increases (decreases) by an amount given by Eq. 11, and the probability to dissociate (form) again increases as compared with the IFE case. Therefore, the basepair hopping effect slows the overall F-U kinetics of the RNA molecule.

Passive-mode force fluctuations

In the PM, the average force exerted upon the system depends on the state of the RNA molecule (Fig. 4). Therefore, at the timescale 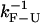associated to the F-U reaction, the average force exerted on the RNA molecule will change by

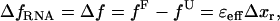(12)

where Δx_r is the change on the RNA extension when the molecule unfolds and ɛ_eff is the effective stiffness of the whole experimental system given by Eq. 5. The force difference (Eq. 12) is a consequence of the particular design of experimental setup (Fig. 1). For longer handles (i.e., softer handles) or softer traps the value of the effective stiffness, and hence the force difference (Eq. 12), decreases. In this latter case, the thermodynamic potential of the whole experimental system (Eq. 1) in ME approaches the IFE case, as shown in the Supplementary Materials (Fig. S1).

The overall effect of such fluctuations in the hopping kinetics is not straightforward because the F-U rates might be increased due to bead-force fluctuations and passive-mode force fluctuations, and also decreased due to the basepair hopping effect. In the limiting case of very soft handles, i.e., when the stiffness of the molecular construct ɛ_x approaches zero (and therefore ɛ_eff = 0), all previous effects of the contributions above tend to disappear and the experimental conditions get closer to the IFE. However, the temporal and the spatial/force sensitivity are also expected to decrease for softer handles (1). The reason is twofold. On the one hand, to measure the F-U rates, the response of the trapped bead must be faster than the F-U reaction, i.e., 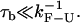The corner frequency of the trapped bead (given by the inverse of Eq. 6) becomes lower for softer handles, decreasing the temporal resolution of the experiment. On the other hand, to detect accurately enough the force/extension jumps that characterize the F-U transition the handles should be stiffer than the trap or ɛ_x ≥ ɛ_b. Otherwise the signal/noise ratio (SNR) would become too low and the experimental signal given by the force/extension jumps could be masked by the handles (1). In the current experimental conditions ɛ_b ∈ [0.035–0.1] pN/nm, whereas ɛ_x ∈ [0.15–1.5] pN/nm, so the inequality ɛ_x ≥ ɛ_b is satisfied. It can be shown that when ɛ_x ≥ ɛ_b, the magnitude of the force fluctuations described in bead-force fluctuations and basepair hopping effect, above, is quite insensitive to the particular value of ɛ_b. The main effect of ɛ_b is to modify the value of the force difference (passive-mode force fluctuations) (Eq. 12), which is minimized by taking ɛ_b as small as possible. Therefore, to get estimates closer to the intrinsic molecular rate, softer traps should be used.

The resolution and limitations of the instrument are also important when acquiring the experimental data. In particular, measurements are sensitive to the bandwidth B at which data are collected and to the time lag of the feedback mechanism, T_lag, as follows.

Limited bandwidth

If the bandwidth B is not higher than the F-U rates, the time resolution of the measurement becomes too low to detect the F-U reaction and the measured kinetic rates will be affected.

Piezoelectric flexure stage

In the CFM, the force-feedback mechanism operates to compensate for the force difference given by Eq. 12. If 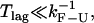then Δ〈f_RNA〉 = 0 is verified and the feedback mechanism can efficiently keep the force constant. Otherwise, the feedback mechanism cannot maintain the force constant on timescales where the molecule folds/unfolds. In the latter case, the feedback mechanism leads to distorted rates. We call this the distortion effect (1).

If B⁻¹ and T_lag are much shorter than 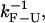only the effects of the bead-force fluctuations, basepair hopping effect, and passive-mode force fluctuations remain. By using longer (i.e., softer) handles and softer traps these effects are also minimized and the measured rates should approach the ideal molecular rates. For all the experimental setups we have investigated in this work, the spatial/force resolution is high enough to detect the F-U reaction (1) and the condition 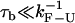holds. Therefore, the optimal conditions to carry out measurements would be to use handles and traps as soft as possible within the limiting resolution imposed by the experimental setup ().

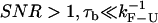Even though current experiments (1) do not reveal the presence of intermediates of the F-U reaction, most of the kinetic effects observed in the experiments are not captured by a simple two-state model that does not include intermediate configurations. In fact, the two-state model only considers the dynamical effects of bead-force and passive-mode force fluctuations, which increase the RNA F-U kinetics as compared with the IFE case. To reproduce the observed dependence in the kinetics it is necessary to take into account the basepair hopping effect in the dynamics. Therefore, a multistate model like the one proposed here, is needed to capture the effect of the experimental setup on the measured kinetics.

MODELING HOPPING DYNAMICS IN THE EXPERIMENTAL MODES

In this section we study the RNA F-U kinetics under the experimental conditions by simulating the dynamics of the whole system in the PM and CFM.

Kinetic model for folding/unfolding the RNA

To model the kinetics of the RNA hairpin we adapt the model by Cocco et al. (23) to our experimental setup; we assume the dynamics of the hairpin to be sequential (see Thermodynamics of the Experimental System). Therefore, one-step transitions connect each configuration n with its first nearest neighbors in the configurational space, n+1 and n−1. The dynamical process is then governed by the kinetic rates to go from n to n′ with n′ = n−1, n+1. This kinetic model is schematically depicted in Fig. 2. The evolution in time of the configuration n of the hairpin is described by a set of coupled master equations as

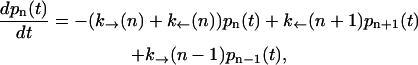(13)

with n = 0,…N and 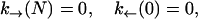p₋₁(t) = 0, p_N+1(t) = 0. The function p_n(t) is the probability for the RNA molecule to be in the configuration n at time t; k_→(n) is the transition rate to go from n to n+1 at time t; and k_←(n+1) denotes the rate of the reverse reaction. The experimental system includes different elements such as the handles, the trapped bead, and the RNA molecule, therefore the F-U kinetics is described by the rates associated to the transitions, 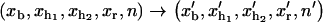with n′ = n−1, n+1, and 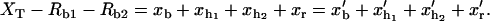Because the bead relaxes much slower than the handles and the ssRNA, the kinetics of the hairpin is slaved to the relaxational dynamics of the bead. Consequently, the kinetics rates can be factorized in two terms as

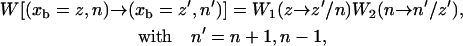(14)

where 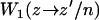is the transition rate to go from x_b = z to x_b = z′ when the hairpin is in the conformation n and 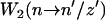is the transition rate to go from n to n′ when x_b = z′. The rates given in Eq. 14 must verify detailed balance,

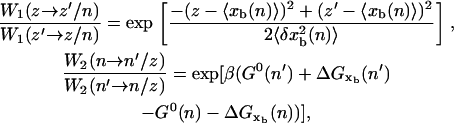(15)

where 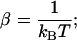〈x_b(n)〉 and 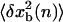are the mean value and the fluctuations in the position of the trapped bead at the given value of the control parameter X_T and at the given configuration of the hairpin n; G⁰(n) is the free energy of the configuration n of the hairpin at zero force; and 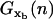is the free energy contribution due to the handles and the ssRNA that are stretched a distance x = X_T − x_b − R_b1 − R_b2. The value 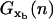is computed by using Eq. 4 as

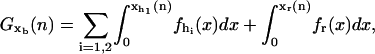(16)

where f_α(x) with α = h₁,h₂,r corresponds to the equilibrium force extension relation as given by the WLC model (24,25). The variables 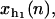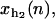and x_r (n), that verify 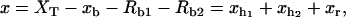correspond to the extension of the handles 1 and 2 and the released ssRNA for the RNA configuration with n opened bps. The choice of the opening and closing rates k_→(n) = W₂(n → n + 1/x_b) and k_←(n) = W₂(n → n – 1/x_b) is based on two assumptions (23):

1. The transition state corresponding to the formation-dissociation reaction of a given bp is located very close to the formed state. Therefore the opening rate k_→ for a given bp depends on the particular bp and its neighbor (i.e., GC vs. AU), but does not depend on the value of the control parameter y (e.g., X_T or f).

2. The rate of closing k_← is independent of the sequence and is determined by the work required to form the bp starting from the dissociated state.

The rates k_→(n), k_←(n) are of the Arrhenius form and are given by

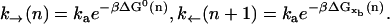(17)

The constant k_a is a microscopic rate that does not depend on the particular bp sequence and is equal to the attempt frequency of the molecular bond. The kinetic process defined by k_→, k_← is of the activated type. The value of k_→ is a function of the free energy difference ΔG⁰(n) = G⁰(n+1) − G⁰(n) between the two adjacent configurations, n and n+1. 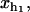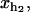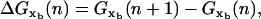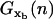The value of k_← depends on the value of the control parameter X_T and on the value of x_b, and x_r through where is the free energy defined in Eq. 16. The choice of these rates has the advantage that there is only one free parameter, k_a, while the rest of parameters can be obtained from measured thermodynamics. This model is an extension of the one proposed by Cocco et al. (23), as given in Eq. 13, by considering the appropriate kinetic rates (Eq. 17) adapted to reproduce the experimental CFM and PM.

Monte Carlo simulation of hopping experiments

To simulate the hopping experiment we benefit from the large separation of timescales between the different elements of the system: τ_b ≫ τ_handles, τ_ssRNA (Table 1). We consider that during the time of an iteration step in the simulation, dt = 10⁻⁸ s, the handles and the ssRNA are in local equilibrium, but the bead in the trap is not. Note that the timescale of iteration is smaller than the relaxation time τ_handles. However, we do not expect our results to change much by taking into account the microscopic dynamics of the handles, because the most important dynamical effect in either the simulations or the experiments comes from the bead in the trap. In fact, the bead is the element of the system with largest dissipation and slowest relaxation rate as compared to the elastic and bending modes of the handles and the ssRNA. In our simulation, we implement the following algorithm:

At each iteration step dt,

1. The position of the bead trapped in the optical potential x_b evolves according to the Langevin dynamics of an overdamped particle (22),

   (18)

   where ɛ_b is the stiffness of the trap, γ is the friction coefficient of the bead, and f_x is the force exerted by the molecular construct on the bead. The value f_x is computed as the force needed to extend the molecular construct (the handles and the ssRNA) a distance x = X_T − x_b − R_b1 − R_b2. The stochastic term ξ(t) is a white noise with mean value 〈ξ(t)〉 = 0 and variance 〈ξ(t)ξ(t′)〉 = 2 k_BT γδ(t − t′). From the evolution of the bead position, given by Eq. 18, we obtain the instantaneous values of the molecular extension x = X_T − x_b − R_b1 − R_b2 and force f = ɛ_b x_b.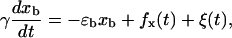

2. For a given extension x = X_T − x_b − R_b1 − R_b2, we compute the equilibrium value of the extension of the handles and the released ssRNA for the configurations with n and n−1 opened bps, by using the WLC model (24,25). We then compute the function 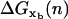as given by Eq. 16.

3. We change the configuration of the hairpin from n to n, n+1 or n−1 with probabilities [1− k_→(n) dt − k_←(n)dt], k_→(n)dt, and k_←(n)dt, respectively, where the rates k_→ and k_← are defined in Eq. 17.

4. Return to 1.

We average the instantaneous data over a bandwidth B. In the CFM, at every 1 ms of time, we increase (decrease) the value of the total end-to-end distance X_T by 0.25 nm if the measured force differs by >0.1 pN below (above) the setpoint force value at which the feedback mechanism operates.

Reaction rates from the hopping traces

In this section, we compute the rates of the F-U reaction from the hopping traces corresponding to the CFM and PM simulations. We then compare them with the experimental results (1). We use the free energy parameters given in the literature (33–35) to compute the free energy landscape at zero force G⁰(n) of the P5ab hairpin at 25°C and in 1 M NaCl. We consider that the mechanical response of the handles and the ssRNA is characterized by a persistence length (P) and contour length (L) equal to P_h = 10 nm, L_h = 0.26 nm/bp for the handles and P_ssRNA = 1 nm, L_ssRNA = 0.59 nm/base for the ssRNA. To analyze the effect of the instrument on the measured rates we study different experimental setups by considering handles of several lengths and optical traps characterized by different stiffness. Note that our experiments were performed at 250 mM NaCl while our simulations used the free energy parameters obtained from the literature (33–35) at 1 M NaCl. The presence of salt in the solvent stabilizes folded conformations of RNA molecules due to the larger screening of the electrostatic repulsion between the phosphates groups. Therefore, the RNA native structure at higher salt concentrations has a lower free energy (i.e., it is more stable) and the critical value of the force for the folding/unfolding reaction is larger. This is in agreement with the fact that the values of the critical force that we obtain in our simulations are ∼1–1.5 pN above the ones measured in the experiments. To reproduce the thermodynamic properties of the RNA molecule from our simulations we must shift the forces by 1–1.5 pN downward. In addition, the salt concentration might also affect the F-U kinetics. The value we estimate for the attempt frequency k_a by fitting simulations and experiments already incorporates the salt correction.

Figs. 3 and 4 show examples of CFM and PM traces obtained from the simulations of the experimental system. The distributions of lifetimes obtained either from the experimental traces or from the simulations have an exponential decay (Supplementary Materials, Fig. S2), as expected for a two-state system. To extract the rates of the F-U reaction in each mode we have analyzed the simulated data using the same methods as for the experimental data (1). We then compare these rates with the experimentally measured rates presented in our companion article (1). The value of the free parameter k_a is chosen to optimize the fit between the rates extracted from the simulation traces and the ones measured in the experiments. For this fit, we used the PM data as explained in the Supplementary Materials (Fig. S3). Notice that the value of k_a fixes the timescale unit of the simulation allowing us to establish the connection between the real microscopic dynamics of the molecule and the mesoscopic description. We get the characteristic bp attempt frequency, k_a = 2.3 × 10⁶ Hz. By solving the master equation (Eq. 13) for the F-U reaction in the IFE (23), we also get an estimate for the intrinsic molecular rate 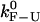at the critical force. We obtain 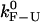= 13 Hz. In what follows, we compare this value with the measured rates in the CFM and PM to infer the optimal conditions to obtain rates as close as possible to the intrinsic molecular rate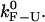

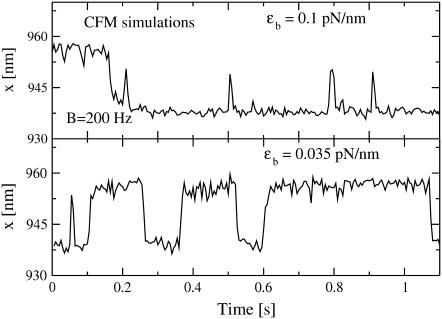
FIGURE 3.

Extension traces for P5ab hairpin with 3.2 Kbp handles in CFM from the simulations for two different trap stiffnesses ɛ_b ≈ 0.1 pN/nm (upper panel) and ɛ_b ≈ 0.035 pN/nm (lower panel). The bandwidth used is 200 Hz.

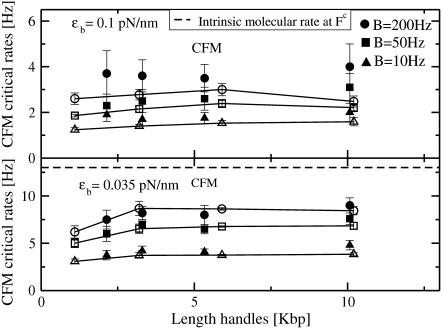
Constant-force mode (CFM)

In Fig. 5, we show the values of the CFM critical rates, 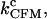obtained from the simulations as a function of the length of the handles (solid symbols) compared with the experimental ones (1) (open symbols connected by lines). The agreement between the experimental and simulation results in the CFM is reasonable. The analysis done in Instrumental Effects predicts that the measured critical rates should converge to the value of the intrinsic molecular rate 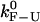for softer handles, i.e., longer handles. This is true when the instrument has enough time resolution to resolve the force/extension jumps, i.e., 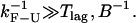However, we do not observe this convergence, neither in the simulations nor the experiments (Fig. 5), probably because in our instrument such that the condition 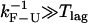is not satisfied. In this situation, the measured rates highly depend on the bandwidth and on the criteria used to analyze the data, i.e., the so-called distortion effect discussed in the companion article (1). We think that the nonconvergence of the measured rates for long handles to the intrinsic molecular rate 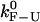arises from distortion effects due to the finite response time of the instrument, T_lag. To validate this hypothesis and to obtain better estimates for the rates, we propose to use the PM data to extract the PM critical rate 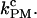In the PM, there is no feedback mechanism; therefore, PM data does not suffer from the distortion effect. Also, by using a bandwidth high enough, i.e., B ≫ k_F-U, we waive the dependence of the measured rates on the bandwidth. Therefore, the PM critical rate 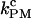should provide a better estimate of the F-U rate at the critical force.

FIGURE 5.

CFM critical rates as a function of the length of the handles from the experiments (open symbols connected by lines) and simulations (solid symbols) for two different values of the trap stiffness ɛ_b = 0.1 pN/nm (upper panel) and 0.035 pN/nm (lower panel). Results obtained by using different bandwidth B = 10, 50, and 200 Hz (circles, squares, and triangles, respectively) are shown. The molecular rate 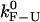(dotted line) is also shown in the bottom panel for comparison. Better results are obtained for the softest trap ɛ_b = 0.035 pN/nm where distortion effects are less important.

Passive mode (PM)

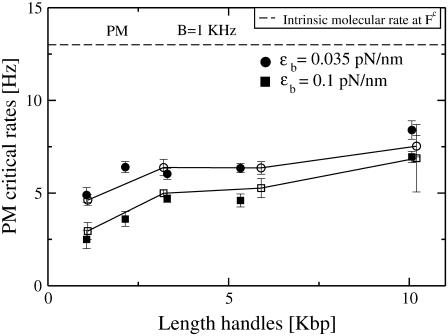
From the PM data, we extract the PM rates. By doing numerical simulations at different values of X_T, we obtain the PM folding and unfolding rates at different forces. As shown in Fig. 6, the logarithm of the PM folding and unfolding rates as a function of the force fits well to a straight line, as predicted by the Kramers-Bell theory for two-state systems (18). The experimental measured rates show the same dependence on the force as the simulation results (Fig. 6), suggesting that the model proposed predicts well the location of the transition state (17). The PM critical rate 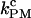is obtained from the intersection of the linear fits to the computed data for ln(k_U) and ln(k_F) as a function of the force. In Fig. 7, we show the measured PM critical rates from the simulation traces (solid symbols) as well as the experimental results (1) (open symbols connected by lines) as a function of the length of the handles. Two sets of data at the trap stiffness ɛ_b = 0.1 pN/nm and ɛ_b = 0.035 pN/nm are shown. Both experimental and simulation results agree pretty well. The bandwidth used, B = 1 KHz, is much greater than k_F-U. Hence, the time resolution is sufficient to follow the F-U reaction, and the measured rates are not affected by the average of the data over the time window B⁻¹. Better estimates are obtained for the softer trap case as expected.

FIGURE 7.

PM critical rates as a function of the length of the handles measured in PM from experiments (open circles connected by lines) and simulations (solid symbols) for two different values of the trap stiffness ɛ_b = 0.1 pN/nm (squares) and 0.035 pN/nm (circles). The bandwidth (1 KHz) is much larger than the characteristic frequency of the F-U reaction. The intrinsic molecular rate 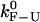(dotted line) is shown for reference. The PM rates show a tendency to approach the value of 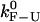for long handles as the analysis done in Instrumental Effects predicts. Better results are also obtained for the softest trap ɛ_b = 0.035 pN/nm. The agreement among the experiments, simulations, and theory is good.

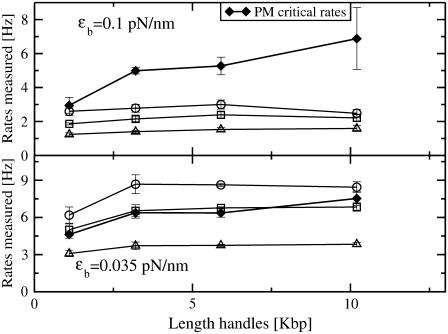
Finally, in Fig. 8 we compare the critical PM (solid symbols connected by lines) and CFM rates (open symbols connected by lines) measured in the experiments. The discrepancy between the critical rates 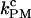and 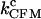is larger for the stiffest trap results (ɛ_b = 0.1 pN/nm, upper panel) and the longest handles, the case in which distortion effects in the CFM are more important (1). Moreover, the values of the rates 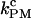obtained from the PM data in both experimental setups (upper and lower panels) increase for longer handles and show a tendency to approach the ideal molecular rate value of 13 Hz as expected (see Instrumental Effects). These results confirm our initial expectations that, when 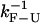is of the order of T_lag, the measured rates in the CFM are strongly affected by the distortion effect.

FIGURE 8.

We compare the experimental CFM critical rates (open symbols connected by lines) with the experimental PM critical rates (solid diamonds connected by lines) for two different trap stiffnesses ɛ_b = 0.1 pN/nm (upper panel) and ɛ_b = 0.035 pN/nm (lower panel). CFM results with bandwidths of 10 Hz, 50 Hz, and 200 Hz are shown in triangles, squares, and circles, respectively.

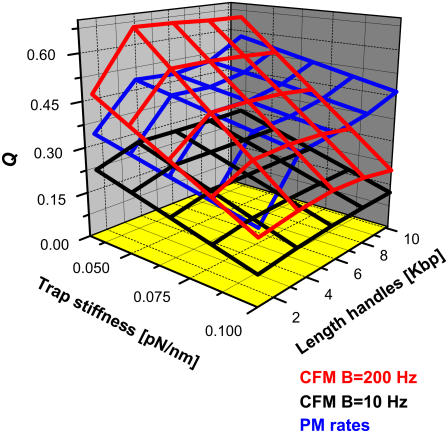
The quality factor Q

To compare different estimates for the critical rates, it is useful to define a parameter that characterizes the reliability of the measurement. We define the quality factor Q as the relative difference between the measured rate (k_est) and the intrinsic molecular rate :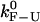

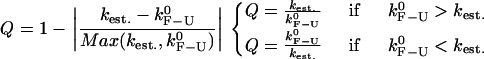(19)

As a compendium of all the results, we show in Fig. 9 the value of Q obtained for the different estimates for the critical rates as extracted from the experimental data. The factor Q is shown as a three-dimensional plot as a function of the length of the handles and the trap stiffness. We show three surfaces, each corresponding to a different estimate of the rates: the CFM critical rates (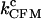) for two different values of the bandwidth, and the PM critical rates ().

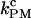FIGURE 9.

We show the quality factor Q (defined as the closeness between the measured rate and the intrinsic molecular rate) obtained from different measured critical rates in experiments as a function of the length of the handles and the trap stiffness. For the CFM experimental results we show the Q corresponding to the CFM critical rates at two different values of the bandwidth, B = 200 Hz (red) and B = 10 Hz (black). The Q for the PM critical rates extracted from PM experiments is also shown (blue). Generally, better measurements (higher Q-values) are obtained from softer traps and longer handles.

Depending on the RNA molecule (sequence, length, folding, and unfolding rates) and the characteristics of the experimental setup (trapped bead, handles, feedback time lag, and bandwidth), the quality factor of each estimate may change. As a general result, we infer that better measurements are obtained for softer traps and longer handles as long as the transition signal is detectable. For fast hoppers (which have F-U rates that are not much slower than the force-feedback frequency, as happens in our study of the P5ab hairpin where 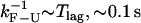), PM rates provide better estimates than CFM rates. On the other hand, for slow hoppers, the PM becomes impractical due to the presence of drift effects. In the latter case, the CFM is efficient and the CFM critical rates should be a good estimate for the intrinsic molecular rates.

SUMMARY AND CONCLUSIONS

In this work, we have introduced a mesoscopic model for the study of the folding/unfolding (F-U) force-kinetics of RNA hairpins in hopping experiments using optical tweezers. The model incorporates the different elements of the experimental setup (bead, handles, and RNA sequence) and limitations of the instrument (time lag of the constant-force mode and finite bandwidth). We carry out numerical simulations of the proposed model and compare them with hopping experiments in the P5ab RNA hairpin reported in our companion article (1). This analysis allows us to extract the value of the microscopic attempt frequency k_a for the dissociation kinetics of individual basepairs. The estimate for k_a is then used to extract the intrinsic molecular rate for the RNA hairpin, 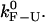We then compare the estimate of the intrinsic molecular rate with the values for the different rates (CFM and PM) obtained under different experimental conditions. The goal of the research is to infer the optimal conditions to extract the intrinsic molecular rate of the RNA molecule using data obtained in the different experimental modes: passive and constant-force. We have considered different values of the stiffness of the trap and different lengths of the handles. Due to the complexity of the system the quality factor Q (defined as the relative difference between the measured rate and the intrinsic molecular rate) will critically depend on various parameters of the instrument (experimental setup and the instrumental limitations) and the molecule.

Through our analysis, we are able to find the optimum experimental conditions to measure hopping rates. Even though our study has been carried out for an RNA hairpin with a fixed sequence in an optical tweezers setup, the methodology and rationale presented here can be applied to other experimental setups, such as dumbbell dual-trap optical tweezers (21,32,36,37), other acid nucleic sequences, or proteins (12). Our main conclusions can be summarized as follows.

Trap

For all experimental modes, it is advisable to use traps as soft as possible (ɛ_b ≤ 0.1 pN/nm). In particular, to detect the force/extension jumps that characterize the F-U transition the trap should not be stiffer than the handles.

Handles

For all experimental modes, it is advisable to use handles as long as possible within the resolution limit of the instrument (3 Kbp ≤ L_h ≤ 10 Kbp):

1. The SNR of the extension/force signal must be large enough to follow the F-U reaction.

2. The corner frequency of the bead (equal to the inverse of its relaxation time) must be much higher than the F-U rate of the hairpin (see Discussion in (1)).

Bandwidth

For all experimental modes, it is advisable that the bandwidth of data collection is as large as possible.

Force-feedback frequency

In the CFM, it is important that the frequency of the force-feedback mechanism is as high as possible. In particular, the force-feedback frequency must be higher than the F-U rate, otherwise distortion effects are big and the force-feedback mechanism becomes inefficient. If the latter restriction is not satisfied (as happens in our study of the P5ab hairpin where 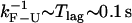) then PM rates provide better estimates than CFM rates. For our experimental setup the CFM should be more efficient in studying slow RNA hoppers (e.g., RNA molecules with tertiary interactions) that satisfy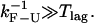

To measure rate constants up to 100 Hz with certain accuracy for RNA molecules of ∼20 bps long, requires traps softer than 0.1 pN/nm, handles longer than 2 Kbp but shorter than 15 Kbp, and bandwidth and force-feedback frequency of 1 KHz or higher. In all cases studied in this work, the different estimates for the rates are of the same order of magnitude as the intrinsic molecular rate. Optical tweezers are, thus, a very useful single-molecule technique to infer the values of the force-dependent F-U kinetic rates of biomolecules. Future design of optical tweezers with higher spatial resolution and higher frequency force-feedback mechanisms will provide better instruments to characterize the F-U kinetics of biomolecules.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.