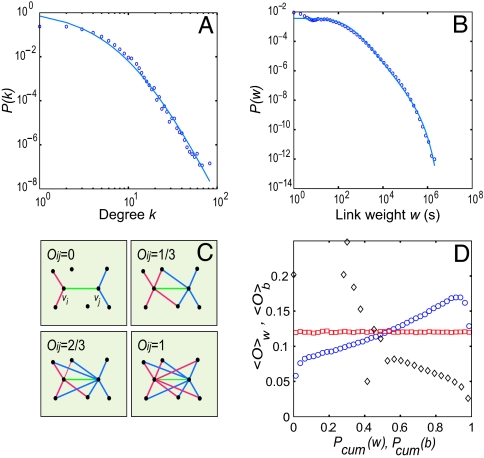
Fig. 1.
Characterizing the large-scale structure and the tie strengths of the mobile call graph. (A and B) Vertex degree (A) and tie strength distribution (B). Each distribution was fitted with P(x) = a(x + x0)−x exp(−x/xc), shown as a blue curve, where x corresponds to either k or w. The parameter values for the fits are k0 = 10.9, γk = 8.4, kc = ∞ (A, degree), and w0 = 280, γw = 1.9, wc = 3.45 × 105 (B, weight). (C) Illustration of the overlap between two nodes, vi and vj, its value being shown for four local network configurations. (D) In the real network, the overlap 〈O〉w (blue circles) increases as a function of cumulative tie strength Pcum(w), representing the fraction of links with tie strength smaller than w. The dyadic hypothesis is tested by randomly permuting the weights, which removes the coupling between 〈O〉w and w (red squares). The overlap 〈O〉b decreases as a function of cumulative link betweenness centrality b (black diamonds).