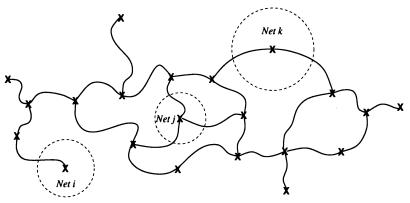
Figure 2.

Large-scale description: “Crosslinked gel.” At large scales, we model RNA secondary structures by replacing each constitutive net with a single vertex. These vertices are connected by single-stranded and double-stranded regions. The large-scale conformational entropy is evaluated assuming that the vertices are connected by Gaussian “springs” whose mean squared elongation in isolation equals the relaxed mean squared distance between the connected nets in question. The conformational entropy of such a “Gaussian crosslinked gel” is then calculated numerically by n − 1 algebraic integrations, where n is the number of vertices and hence nets on the secondary structure. (In some cases, two vertices are connected by several stems, in which case we treat them as springs in parallel and lump accordingly.) To better agree with known structures as described in the text, we crudely incorporate excluded volume effects at this large scale by redefining the equilibrium elongation of the “springs” with an excluded volume exponent of 0.65 (vs. 0.5 for the ideal chain).