Similarity of Traveling-Wave Delays in the Hearing Organs of Humans and Other Tetrapods

Abstract

Transduction of sound in mammalian ears is mediated by basilar-membrane waves exhibiting delays that increase systematically with distance from the cochlear base. Most contemporary accounts of such “traveling-wave” delays in humans have ignored postmortem basilar-membrane measurements in favor of indirect in vivo estimates derived from brainstem-evoked responses, compound action potentials, and otoacoustic emissions. Here, we show that those indirect delay estimates are either flawed or inadequately calibrated. In particular, we argue against assertions based on indirect estimates that basilar-membrane delays are much longer in humans than in experimental animals. We also estimate in vivo basilar-membrane delays in humans by correcting postmortem measurements in humans according to the effects of death on basilar-membrane vibrations in other mammalian species. The estimated in vivo basilar-membrane delays in humans are similar to delays in the hearing organs of other tetrapods, including those in which basilar membranes do not sustain traveling waves or that lack basilar membranes altogether.

INTRODUCTION

Transduction of sound in mammalian ears is mediated by basilar-membrane (BM) waves exhibiting delays that increase systematically with distance from the cochlear base. Fragmentary estimates of such traveling-wave delays exist for several species [see Table 2 in Robles and Ruggero (2001)]. Recently, a nearly complete map of delays, the first for any mammalian species, was drafted on the basis of correlated in vivo BM and auditory nerve measurements in chinchilla (Siegel et al. 2005). Siegel et al. also presented tentative maps for the cochleae of cats and guinea pigs (Siegel et al. 2005). A map of cochlear delays in living humans would be of immense interest but it is impossible to obtain using in vivo measurements such as recordings of BM vibrations or individual auditory nerve fibers: such recordings are highly invasive using current methods and will probably remain undoable in the foreseeable future.

Delays of BM waves were first measured in the temporal bones of human cadavers more than 60 years ago (von Békésy 1943), but, with rare exceptions, most contemporary accounts of BM delays in humans have ignored measurements in temporal bones in favor of indirect estimates based on brainstem-evoked responses (BSERs), compound action potentials (CAPs), and otoacoustic emissions (OAEs). Some of those estimates led to assertions that BM delays are much longer in humans than in common experimental animals (Neely et al. 1988; Shera et al. 2002). Here, we dispute those assertions, showing that all indirect estimates of BM delays in humans, including those used to justify the assertions, are flawed or are not yet adequately calibrated against BM measurements. We also show that estimates of in vivo BM delays in human cochleae, obtained by correcting postmortem BM data according to the effects of death on BM vibrations in experimental animals, are very similar to delays in the hearing organs of other mammals and in nonmammalian tetrapods, including those in which BMs do not sustain traveling waves or that lack BMs altogether.

MATERIALS AND METHODS

Estimates of cochlear delays in humans and experimental animals were drawn from the literature. Delay estimates not explicitly stated in texts or tables were computed from data extracted from figures by digitization (digiMatic, FEB Software, Chesterfield, VA, USA).

RESULTS

Measures of BM delays

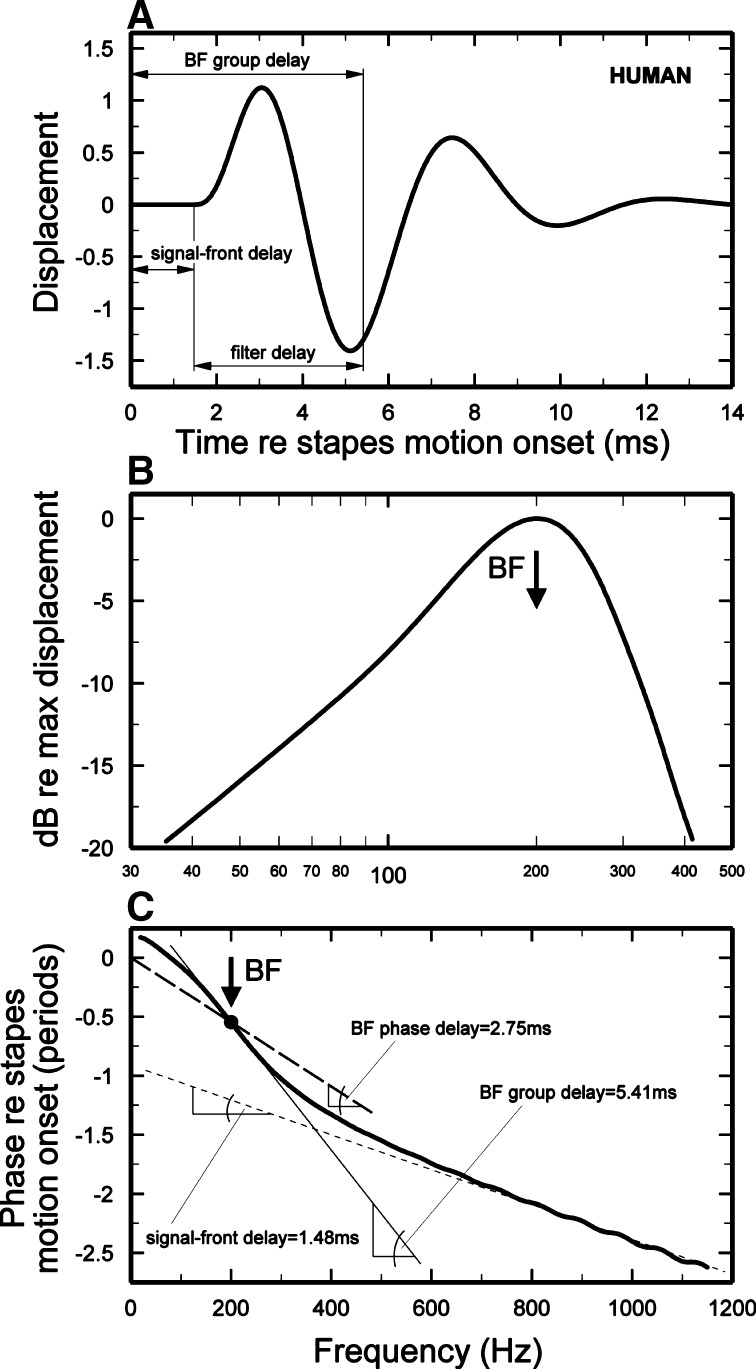
In the analysis of linear systems, three measures of delay are commonly used (Fig. 1): phase, signal-front, and group [pp. 134–136 of Papoulis (1962)]. Although BM responses in healthy cochleae are nonlinear, the same concepts apply (Goldstein et al. 1971; Recio and Rhode 2000; Ruggero 1980). The phase delay is the phase lag at any given frequency expressed in units of time (Fig. 1C). The signal-front delay, a frequency-independent delay, is the latency of the impulse response (Fig. 1A). In many linear systems, the signal-front delay can be measured as equally well as the negative of the high-frequency asymptotic slope of the phase-vs.-frequency function (Fig. 1C) (Brillouin 1960; Goldstein et al. 1971; Papoulis 1962; Recio et al. 1998; Ruggero 1980). However, this procedure cannot be performed using BM data because its phase curves are terminated by high-frequency plateaus (Robles and Ruggero 2001). Other authors have obtained estimates of signal-front delays from the slope of the low-frequency segment of phase-vs.-frequency curves (Robles et al. 1976; Ruggero 1994). Although such estimates correctly matched the directly measured signal-front delays at the 7-kHz site of the squirrel monkey cochlea (Robles et al. 1976), theoretical considerations indicate that they overestimate the signal-front delays measured with clicks (Papoulis 1962); see also Figure 1 of (Ruggero 1980).

FIG. 1.

Delays in BM vibrations at the 200-Hz site of the human cochlea. A Impulse response synthesized on the basis of von Békésy’s measurements of the latencies of BM responses to clicks (von Békésy 1949a) and of the magnitudes and phases of responses to tones (von Békésy 1947) in the cochleae of human cadavers. The signal-front delay is the latency of cochlear responses to clicks, measured from the onset of stapes motion [Fig. 11 of von Békésy (1949a)]. The BF group delay, the center of gravity of the impulse response, equals the signal-front delay plus the filter delay. The filter delay corresponds to a minimum-phase impulse response [Figs. 7 and 9 of Flanagan and Bird (1962)] computed on the basis of responses to tones (von Békésy 1947). B Spectral magnitudes of the impulse response of A. C Phase-vs.-frequency curve for the impulse response of A. The negative slope around BF (C) is identical to the center of mass of the impulse response (A). The negative slope of the high-frequency asymptote (C) is identical to the signal-front delay (A). Phase delay is the phase lag expressed in units of time or, equivalently, the negative slope of a straight line connecting a phase-frequency point and the origin (C).

In experimental animals, the signal-front delay remains unaltered postmortem at both basal [e.g., Fig. 1 of Ruggero (1994); Fig. 14 of Recio et al. (1998)] and apical (Cooper and Rhode 1996; Zinn et al. 2000) cochlear sites. In other words, the signal-front delay is a “passive” property of BM responses [see review by Ruggero (1994)]. Following von Békésy, we equate signal-front delay to BM travel time [see Fig. 11 of von Békésy (1949a) and p. 2293 of Recio and Rhode (2000)]. Hence, in vivo traveling-wave delay can be measured postmortem, as von Békésy did in the case of the human cochlea [Fig. 11 of von Békésy (1949a)].

The group delay at any particular frequency is the negative of the slope of the phase-vs.-frequency function at that frequency. For BM responses to low-level stimuli in mature healthy cochleae, the CF group delay coincides with the weighted-average group delay (the “center of mass”) of the impulse response. [Following Overstreet et al. (2002a, b), we distinguish between best frequency (BF) and characteristic frequency (CF). Best frequency is the stimulus frequency producing the largest response (without regard to stimulus level or cochlear health or development). Characteristic frequency is the BF of responses to low-level stimuli in mature and healthy cochleae.] For higher stimulus levels at the base of the cochlea, both the CF group delay and the weighted-average group delay become shorter, the latter at a greater rate than the former due to the increasing weight of low-frequency regions, which have low group delays [see Fig. 1 of Ruggero (1994)]. In BM responses, the CF group delay is partly an “active” property because its exact value in vivo depends on the health of the cochlea and on the stimulus level (Recio et al. 1998; Ruggero et al. 1997). Postmortem, the CF group delay does not vary as a function of stimulus level and is nearly the same as the CF group delay for very intense stimuli in vivo.

The phase delay, signal-front delay, and BF group delay are illustrated in Figure 1, which is based on von Békésy’s BM measurements in human temporal bones at the cochlear site with BF of 200 Hz. Figure 1A shows a delayed version of a minimum-phase impulse response [Figs. 7 and 9 of Flanagan and Bird (1962)] computed by Flanagan and Bird on the basis of von Békésy’s amplitude data for responses to tones (von Békésy 1947). The minimum-phase impulse response has been delayed by 1.48 ms, the travel time (i.e., the signal-front delay) measured by von Békésy using responses to clicks [Fig. 11 of von Békésy (1949a)]. After the signal-front delay, the BM “rings” with a period of 5 ms (=1/BF; Fig. 1B). Note that the near-BF group delay is the sum of the signal-front delay and a filter delay [or “resonance build-up time” (de Boer and Nuttall 1996)].

BM delays in experimental animals

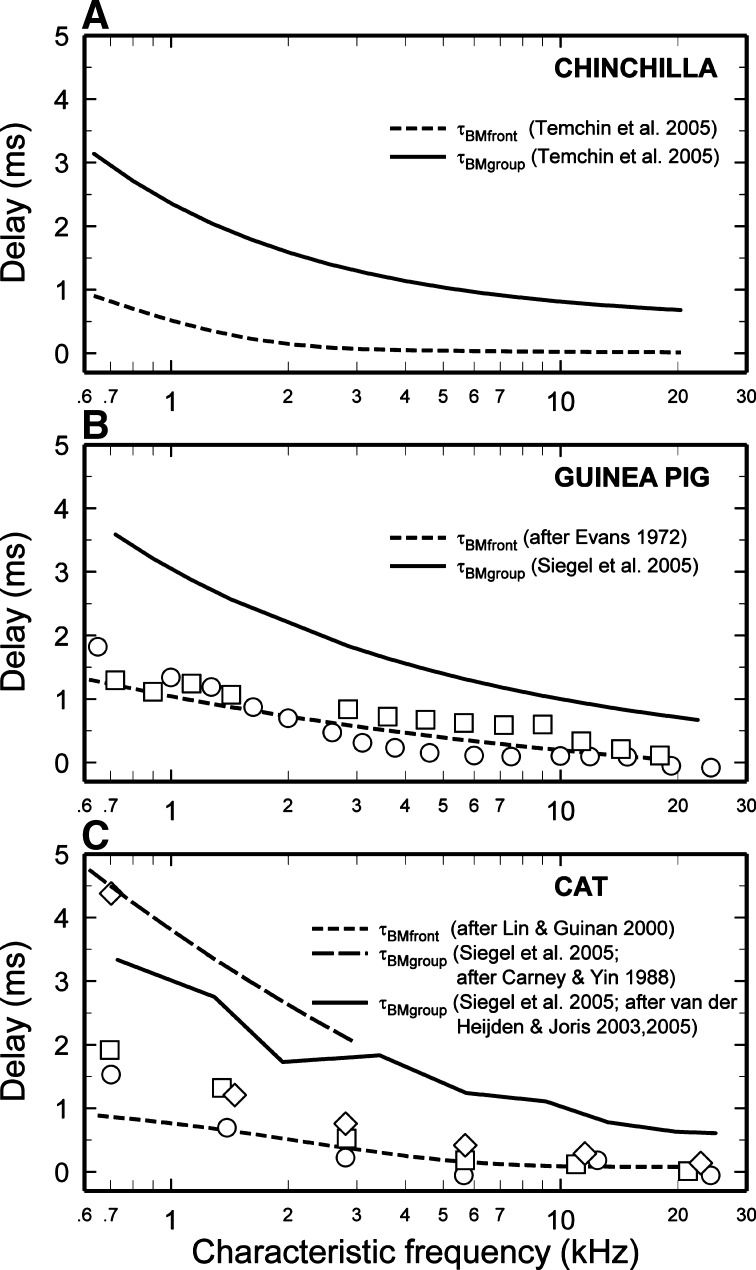
Direct measurements of BM delays in healthy cochleae are available only for a few basal sites in several mammalian species [for review, see Robles and Ruggero (2001)] and single apical sites in chinchilla (Cooper and Rhode 1996) and guinea pig (Zinn et al. 2000). The direct measurements in chinchilla were recently supplemented by extensive estimates of BM delays derived from responses of auditory nerve fibers (Temchin et al. 2005). The signal-front and CF group delay estimates derived from auditory nerve fibers, fully consistent with direct BM measurements at both basal and apical sites, have permitted drafting nearly complete maps of cochlear delays in chinchilla, the first for any species (Temchin et al. 2005). The CF group delay maps are indicated by the black solid lines in Figures 2A, 7, and 8. A CF group delay map for cat (solid and long-dash lines in Fig. 2C and blue solid lines in Fig. 8), still uncorroborated by direct BM recordings, was proposed (Siegel et al. 2005) on the basis of published auditory nerve data (Carney and Yin 1988; van der Heijden and Joris 2003; van der Heijden and Joris 2005). A more conjectural map for guinea pig (solid line of Fig. 2B and green solid line in Fig. 8) was drafted (Siegel et al. 2005) by adjusting an equation with the same form as the equations for cat and chinchilla to fit direct BM measurements at several basal sites and a single apical site (Zinn et al. 2000).

FIG. 2.

Cochlear delays in chinchilla, cat, and guinea pig. Estimates of BM signal-front (short-dash lines) and CF group delays (solid and long-dash lines) based on direct BM recordings and/or recordings from auditory nerve fibers. [Note that the delays of responses of auditory nerve fibers corrected for neural/synaptic delays of 1 ms coincide with the delays of direct BM recordings (Temchin et al. 2005).] A Average signal-front and CF group delays for chinchilla BM (Temchin et al. 2005). B Derived-band estimates for guinea pigs from Figure 6 of Shore and Nuttall (1985) (click level is not specified) and Figure 3 of Aran and Cazals (1978) [click level is 65 dB pe SPL (50 dB HL)]. Solid line, from Figure 7A of Siegel et al. (2005). Dashed line, from data of Figure 1 of Evans (1972). C Derived-band delay estimates (open symbols) from a single cat from Figure 3 of Evans and Elberling (1982). Clicks were presented at 30, 50, and 70 dB above the CAP threshold (defined as the level that evoked a CAP with average peak-to-peak amplitude of 5 μV). Solid and long-dash lines from Figure 7B of Siegel et al. (2005), based on data of Carney and Yin (1988), van der Heijden and Joris (2003), and van der Heijden and Joris (2005). Short-dash line, from Figure 6A of Lin and Guinan (2000).

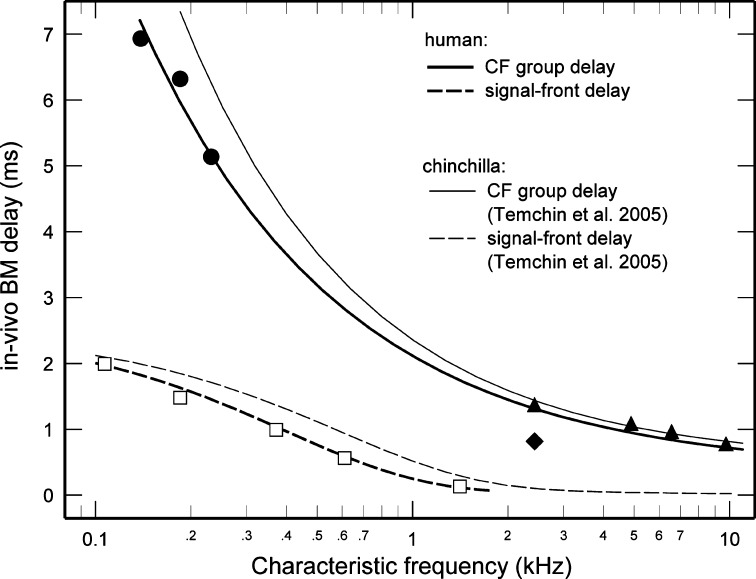
FIG. 7.

In-vivo BM delays in the cochleae of humans and chinchillas. Open symbols indicate signal-front delays for humans, which are the same in vivo and postmortem. Chinchilla signal-front delays (thin dashed lines) from Figure 13A of Temchin et al. (2005). Filled symbols indicate in vivo CF group delays for humans obtained by correcting the postmortem data (Fig. 5) for the effects of death (Fig. 6). In vivo chinchilla near-CF group delays (thin solid line) from Figure 13B of Temchin et al. (2005).

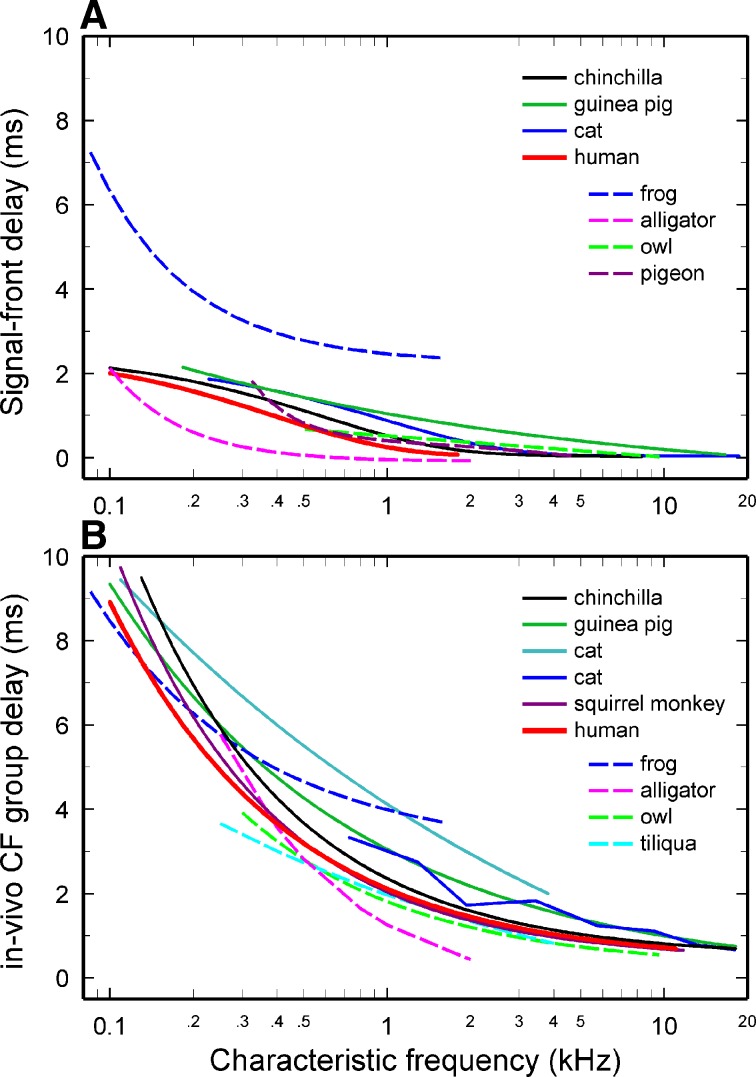
FIG. 8.

Delays in the hearing organs of humans and other tetrapods. A Signal-front delays. B CF group delays. Chinchilla: Figure 13B of Temchin et al. (2005). Guinea pig: signal-front delay, Figure 1 of Evans (1972); group delay, Figure 7A of Siegel et al. (2005). Cat: Figure 7B of Siegel et al. (2005) after Carney and Yin (1988), van der Heijden and Joris (2003), and van der Heijden and Joris (2005). Frog: signal-front and group delay, Figure 14 of Hillery and Narins (1987). Alligator: group delay, Figure 11 of Smolders and Klinke (1986); signal-front delay, Figure 9 of Smolders and Klinke (1986). Tiliqua rugosa: data Figure 9A of Manley et al. (1990). Barn owl: group delay, Figure 10A (55–65 dB) of Köppl (1997b); signal-front delay, Figure 7 of Köppl (1997a). Pigeon signal-front delay: Figure 11 of Sachs et al. (1974). Monkey group delay: curve synthesized from responses of auditory nerve fibers with CFs lower than 1.5 kHz, from Figure 3 of Anderson et al. (1971), and BM responses at sites with CF 7–8 kHz, from Table I of Rhode (1978). In all cases, trend lines indicate CF-dependent cochlear mechanical delays (i.e., after correcting for middle-ear delays and, in the case of neural data, after correcting for synaptic and neural-conduction delays, as estimated in each publication).

The putative derivation of BM delays in humans from OAE group delays

Shera et al. (2002) used the group delays of stimulus-frequency OAEs (SFOAEs) to estimate the CF group delays of BM responses and concluded that BM delays are much longer in humans than in common experimental animals [e.g., three times longer than in cats or guinea pigs for the 3-kHz cochlear site according to Fig. 2 of Shera et al. (2002)]. They based that conclusion on the fact that SFOAE group delays are much longer in humans than in experimental species (Shera et al. 2002) and on the assumption that “the group delay of SFOAEs is equal to twice the group delay of the BM mechanical transfer function evaluated at the cochlear location with CF equal to the stimulus frequency” [page 3319 of Shera et al. (2002)]. Recently, Siegel et al. (2005) tested the assumption of Shera et al. (2002) by comparing SFOAE and BM group delays in chinchilla, cat, and guinea pig and found that, in those species, SFOAEs actually have group delays either similar to or lower than the near-CF BM group delays. That finding contradicts the aforementioned assumption [page 3319 of Shera et al. (2002)] for the species tested and suggests that the assumption is also invalid for estimating BM delays in other species, including humans.

Some investigations estimated BM delays in humans using the group delays of 2f₁–f₂ distortion-product OAEs (DPOAEs) stimulated by one tone with fixed frequency and another with variable frequency (Bowman et al. 1997; Ramotowski and Kimberley 1998; Schoonhoven et al. 2001). The estimates were based on the assumption that the DPOAE group delays for f₂ or f₁ sweeps amount to twice the CF group delay of the BM traveling wave. Such assumption has been shown to be invalid for chinchilla, guinea pig, and gerbil, in which DPOAE and BM group delays are actually similar (Gong et al. 2005; Narayan et al. 1998; Ren 2004; Ren et al. 2006; Ruggero 2004). Thus, it is likely that the assumption is also invalid for humans.

The putative derivation of BM delays in humans from BSER latencies

Neely et al. (1988) estimated BM delays in humans from the wave-V latencies of BSERs to tone-bursts. Latencies were assumed to consist of sums of a constant (i.e., independent of stimulus level and frequency) neural component and a BM component, which varied strongly with stimulus level and frequency. Neely et al., recognizing that their BM delay estimates [e.g., 9 ms for 1-kHz tones presented at 20 dB sound pressure level (SPL)] were “much longer than most previously reported values,” suggested that humans have “longer cochlear travel times than most experimental animals” because “human subjects have longer, more compliant cochleas” (Neely et al. 1988). We show here that the long delay estimates actually resulted from flawed methodology and interpretation.

The interpretation of their data by Neely et al. (1998) was flawed because they incorrectly assumed that the large variation of BSER latency with stimulus level reflects solely BM nonlinearities and, therefore, that BM latencies can be simply estimated from changes in BSER latencies that accompany changes is stimulus levels. In fact, the variation of latency as a function of stimulus level is substantially smaller for BM or inner hair cell responses to CF tone bursts than the variations reported by Neely et al. (1988) for BSERs. For example, for 800-Hz tones, BSER latencies decreased by 5.4 ms in the range 30–90 db SPL [Fig. 2 of Neely et al. (1988)]. In the same level range, inner hair cell receptor potentials elicited by 800-Hz (CF) tones change by only 2.2 ms [as estimated from Fig. 5 of Dallos (1985)], i.e., less than half of the latency change in BSERs. In the range 30–70 dB SPL, BSER latencies to 8-kHz tones change by 1.6 ms. In contrast, BM latencies in responses to 10-kHz CF tones [measured at a velocity of 0.1 mm/s from Fig. 1 of Ruggero et al. (1997)] change by only 0.7 ms, or less than half the latency change in BSERs for 8-kHz tones. To summarize, the BSER intensity-dependent latency changes in humans amount to at least twice the corresponding BM or inner hair cell latency changes in experimental animals.

From the foregoing, it is clear that at least one half of the measured BSER latencies either was a methodological artifact (see below) and/or originated at sites of the auditory pathway more central than the inner hair cells. Recordings from auditory nerve fibers and cochlear nucleus neurons suggest that those sites are the synapses between inner hair cells and auditory nerve terminals. In the 30–90 dB SPL range, with onset stimulus ramps of 1.4 ms, intensity-dependent first-spike latency changes of auditory nerve fibers can be as large as 90 ms [Fig. 4A of Heil and Irvine (1997)]. In the same level range, using 6 ms on ramps, Kitzes et al. (1978) documented first-spike latency changes of about 30 ms in responses of cochlear-nucleus neurons to CF tones (11.6 and 1.8 kHz) [Figs. 1 and 3 of Kitzes et al. (1978)].

The methodology of Neely et al. (1988) was flawed because the durations of the stimulus-onset ramps were not constant across stimulus frequencies. Brainstem-evoked responses to tone bursts consist of neural activity synchronized by short stimulus-onset ramps. Therefore, to validly compare the latencies of responses to different tone bursts, the onset ramps must have a constant duration. In contrast, Neely et al. (1988) used tone bursts with onset-ramp durations that decreased as a function of increasing frequency (e.g., 4 ms for 0.25 and 0.5 kHz, 2 ms for 1–2 kHz, 1.4 ms for 3 kHz, 1 ms for 4 kHz, and 0.5 ms for 8 kHz), which should artificially produce delays that increase as stimulus frequency decreases (Neely et al. 1988). According to the aforementioned study by Heil and Irvine (1997) on auditory nerve fibers, for 30-dB SPL tones, lengthening ramp duration from 1.7 to 4.2 ms can increase first spike latency by 1.5–3 ms [Figs. 2E and 3E of Heil and Irvine (1997)]. Between 0.5 and 3.5 kHz, Neely et al. (1988) found a BSER latency change of 5.9 ms for tone bursts presented at 30 dB SPL. The latency effects documented by Heil and Irvine suggest that between 1.5 and 3 ms (i.e., 25–50%) of the 5.9-ms latency change can be attributed solely to differences in ramp duration (and, therefore, were not due to cochlear travel time). To summarize, the large dependencies of latency on stimulus frequency and level reported by Neely et al. include large, probably dominant, components that did not reflect BM latency shifts but rather were due to the different durations of the onset ramps and to level-dependent variations in first-spike latency of auditory nerve fibers.

Estimation of cochlear delays in experimental animals using derived-band CAPs

Teas et al. (1962) devised a so-called derived-band method that permits extracting some CF-specific information from click-evoked CAPs (Teas et al. 1962): CAPs evoked by clicks presented with a high-pass noise are subtracted from CAPs evoked by clicks presented with a high-pass noise with higher-frequency cut-off. Such derived-band responses, presumably reflecting synchronized firings of auditory nerve fibers with CFs in the frequency range between the two cut-offs, have latencies that vary as a function of frequency in a manner reminiscent of BM delays (Teas et al. 1962).

Early comparisons of derived-band CAP latencies and responses to clicks of auditory nerve fibers in guinea pigs (Prijs and Eggermont 1981) and in a single cat (Evans and Elberling 1982) suggested that such latencies were CF-specific for CFs higher than 1–2 kHz but could not test their accuracy rigorously because reliable measures of BM delays were not available. We now take advantage of newly available maps of BM delay for cat and guinea pig to compare them with derived-band delay estimates.

Figure 2C permits comparing derived-band delay estimates for cat with BM CF group delays and signal-front delays, i.e., the latencies of auditory nerve fiber responses to intense rarefaction clicks, corrected for a neural/synaptic delay of 1 ms [see p. 389 of Ruggero and Rich (1987) and Figs. 2 and 7 of Siegel et al. (2005)]. For the cat cochlea, derived-band delays are shorter than CF BM group delays but similar to signal-front delays. For guinea pig (Fig. 2B), the derived-band delays also approximate the signal-front delays closely. These results, which are consistent with the strong skew toward short delays evident in responses to intense clicks at the BM (Recio et al. 1998) and (even more pronouncedly) in poststimulus histograms of auditory nerve fibers (Kiang et al. 1965; Lin and Guinan 2000), suggest that when implemented with intense stimuli the derived-band method estimates BM signal-front delays for CFs higher than 1–2 kHz.

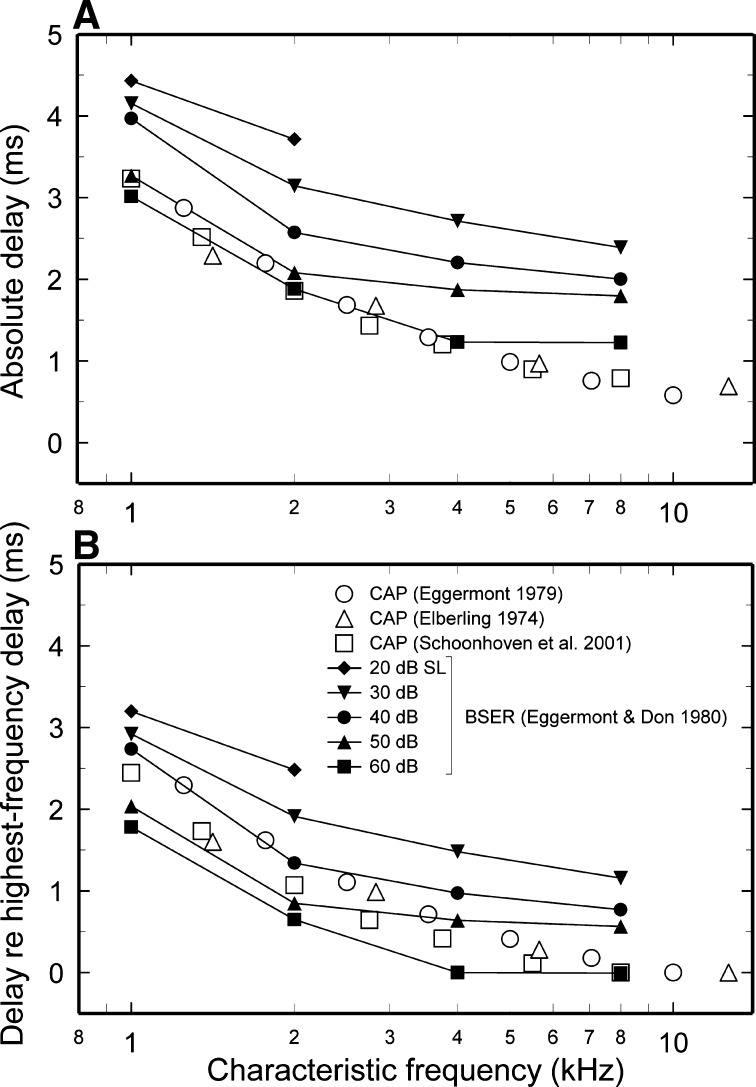
Derived-band delay estimates for the human cochlea

Figure 3A shows BM delay estimates for humans based on derived-band CAPs measured with intense stimuli (open symbols) as well as BSERs measured with stimuli presented at several levels (filled symbols). The BM delay estimates were computed in the original publications by subtracting 0.8 ms from the latencies of the derived-band responses to clicks, on the assumption that synaptic and neural-conduction delays amount to 0.8 ms. Observations listed below suggest that such a procedure is incorrect.

FIG. 3.

Estimates of cochlear delays in humans based on derived-band CAPs and BSERs. A Estimates from CAPs: from Figure 4 of Elberling (1974), Figure 5 of Eggermont (1979), and Figure 3C of Schoonhoven et al. (2001). Estimates from BSERs: Figure 4 of Eggermont and Don (1980). Click levels were as follows: Elberling (1974), 95 dB p.e. SPL (i.e., “baseline-to-peak pressure corresponding to that of a tone with rms pressure of 95 dB SPL”); Eggermont (1979), 90 dB p.e. SPL; Schoonhoven et al. (2001), 98.4 p.e. SPL. The BM delay estimates of Eggermont (1979) and Schoonhoven et al. (2001) were calculated in the original publications on the assumption that synaptic/neural delays amount to 0.8 ms. The delays estimated by Elberling (1974) were not corrected for synaptic/neural delays in the original publication and are presented here after subtraction of 0.8 ms. B All conventions as for A, except that the derived-band measurements are presented relative to the minimum delay for each series of measurements.

(1) In experimental animals, CAPs evoked by intense clicks principally reflect the activity of basal spiral ganglion cells. Therefore, the CAP latency matches the average first-spike latency of responses of high-CF auditory nerve fibers [e.g., Fig. 16 of Kiang (1984) and Fig. 5.14 of Kiang et al. (1965)]. (2) That latency, about 1 ms, exceeds by about 1 ms the (very short) BM signal-front delay at the base of the cochlea [e.g., about 30 μs at the 10-kHz place in chinchilla (Recio et al. 1998; Recio and Rhode 2000)]. (3) As a corollary of 1 and 2, BM travel time (i.e., signal-front delay relative to stapes motion) to any given CF region can be accurately estimated by subtracting the latency of responses of high-CF fibers from the latency of responses of fibers with appropriate CF (Kiang et al. 1965; Ruggero and Rich 1987). (4) As another corollary of 1 and 2, BM travel time in experimental animals can be estimated equally well by subtracting the latency of derived-band CAPs for the highest CFs from derived-band estimates for lower CFs. (5) Presumably, the same procedure should apply equally well for estimating travel time from derived-band delays in humans.

Figure 3B shows the result of subtracting from the derived-band estimates of Figure 3A the minimum latency in each of the corresponding experimental series, which generally corresponds to the derived-band latencies for the highest CF. For high CFs, the delays expressed relative to the delays at the most basal cochlear sites are, by definition, near zero. This result is consistent with the high traveling wave velocities at the base of the human cochlea (e.g., about 20 m/s at the 10-kHz place), as estimated from derived-band CAPs [see Fig. 9 of Eggermont (1976)]. For lower CFs, the derived-band delays for humans grow larger.

The BSER derived-band estimates (Eggermont and Don 1980) of Figure 3B (filled symbols) appear to be the only ones that have addressed the intensity dependence of derived-band delays. For stimulation with intense clicks, derived-band delays measured with BSERs and CAPs are similar and very short (see also Schoonhoven et al. 2001). For lower click levels, delays grow systematically larger. The intensity dependence of derived-band BSER delays is qualitatively consistent with the large intensity dependence of the weighted-average group delay of responses to clicks of auditory nerve fibers [e.g., Figs. 5.9 and 5.10 of Kiang et al. (1965)], which exaggerates the intensity dependence of BM weighted-average group delays [see Fig. 1 of Ruggero (1994)]. Thus, derived-band delays may reflect BM CF group delays at low stimulus levels and signal-front delays at intense levels. However, the precise relationship between BM delays and derived-band estimates cannot be specified at present with any certainty. Given such uncertainty, it seems clear that before derived-band CAPs can be used to estimate BM delays in humans, derived-band CAPs must first be adequately calibrated against BM delays in experimental animals, particularly with regard to their intensity dependence.

BM delays in the cochleae of human cadavers

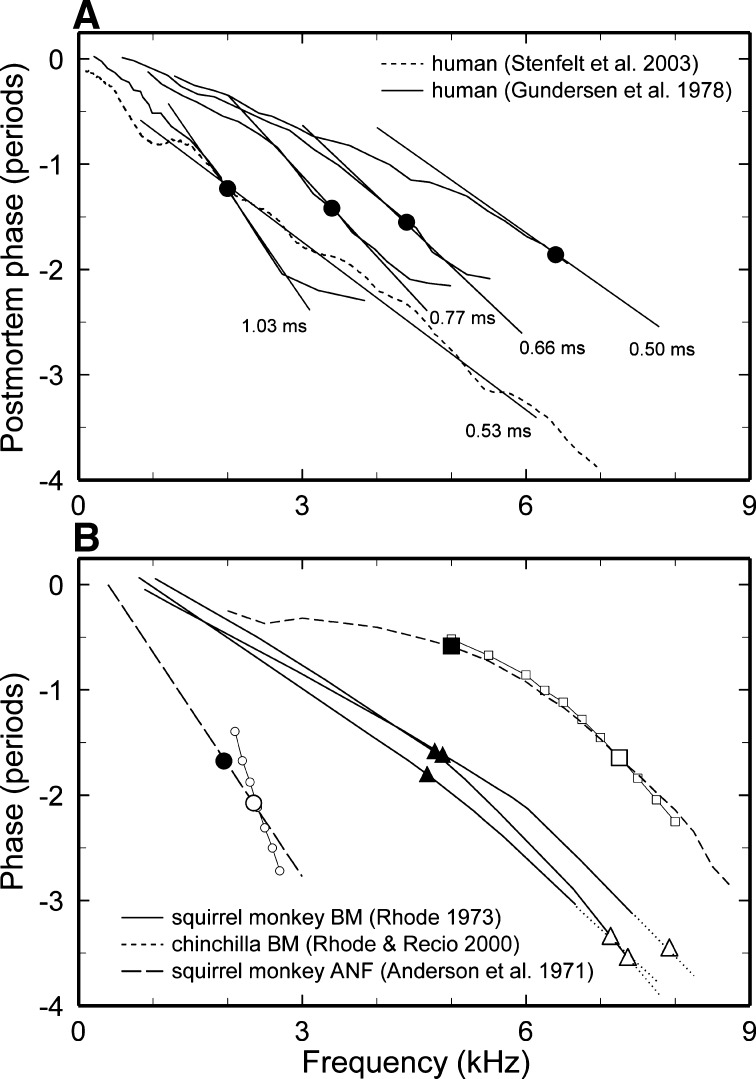
Fortunately, it is not necessary to rely solely on indirect methods to estimate BM delays in the cochleae of living humans. Measurements of BM response phases in human cadavers have existed in the literature since 1943 (von Békésy 1943) but, with rare exceptions (Zwislocki 2002), contemporary discussions of cochlear delays in humans have either failed to take them into account (e.g., Bowman et al. 1997; Donaldson and Ruth 1993; Eggermont et al. 1991; Kimberley et al. 1993; Schoonhoven et al. 2001; Serbetcioglu and Parker 1999; Shera et al. 2002) or dismissed them as unrepresentative of in vivo mechanics [p. 652 of Neely et al. (1988)]. Phase-vs.-frequency curves for postmortem BM responses in human cochleae at apical and at more basal sites are shown in Figures 1C and 4A, respectively.

FIG. 4.

Phase-vs.-frequency curves for cochlear responses in humans, squirrel monkey and chinchilla. A Phase-vs.-frequency curves for BM responses to tones in human cadavers; from Figure 3 of Gundersen et al. (1978) and Figure 5B of Stenfelt et al. (2003). Filled circles, BFs. The straight solid lines have slopes corresponding to BF group delays, indicated in milliseconds. B Phase-vs.-frequency curves for squirrel monkey and chinchilla cochleae. Data for squirrel monkey include postmortem BM responses at sites with BFs of about 4.7 kHz [from Figs. 2, 3, and 4 of Rhode (1973)] and phase-vs.-frequency curves for responses of an auditory nerve fiber (ANF; CF: 2.3 kHz) to 50- (circles) and 90-dB SPL tones (long dashed line). To estimate BM phases, the ANF data [from Figs. 3 and 8 of Anderson et al. (1971)] were corrected for 1 ms, the synaptic/neural conduction delay. The dotted lines are extrapolations of the measured curves. In vivo chinchilla BM responses to 30- (squares) and 80-dB SPL (short-dash line) tones [from Figs. 2E and F of Rhode and Recio (2000)]. Large filled symbols, phase at BF. Large open symbols, phase at CF.

For comparison with the human data of Figure 4A, B shows phase-vs.-frequency curves for cochlear responses in squirrel monkey and chinchilla cochleae. The responses were recorded at sites with CFs comparable to those of Figure 4A. For squirrel monkey, phase-vs.-frequency curves are for postmortem BM responses at sites with BFs near 4.7 kHz (solid lines and triangles) and in vivo responses (corrected for synaptic and conduction delays) of an auditory nerve fiber with CF of 2.3 kHz to tones presented at 50 (open circles) and 90 dB SPL (dashed line). Figure 4B also shows phase curves for chinchilla in vivo BM responses to tones presented at 30 (open squares) and 80 dB SPL (short-dash line). The neural curves for squirrel monkey and the BM curves for chinchilla illustrate that, either in vivo or postmortem, CF group delays for responses to intense stimuli are shorter than in vivo responses to low-level stimuli. The responses for humans and squirrel monkey differ from those in chinchilla in having nearly straight-line phase-vs.-frequency curves. The difference between the curves for primates and rodents probably reflects both species dissimilarities and variation of the phase-vs.-frequency curves as a function of CF [see Pfeiffer and Molnar (1970) and p. 1319 of Robles and Ruggero (2001)].

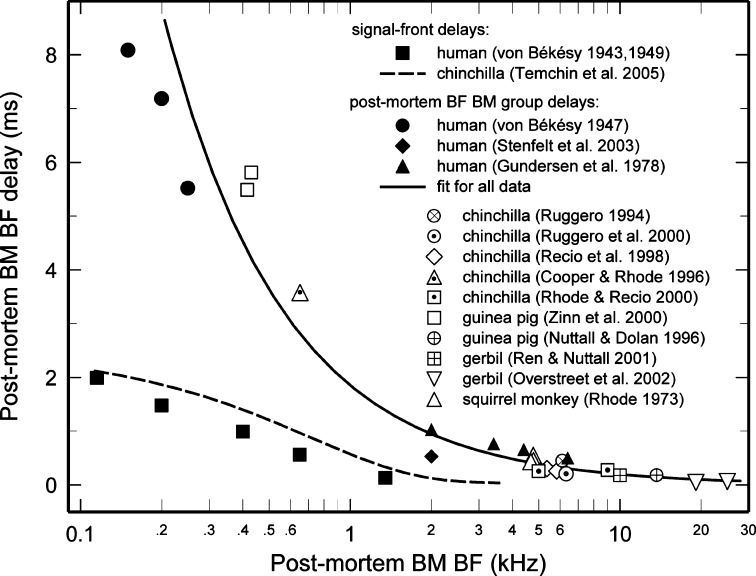
The only direct measurements of signal-front delays for humans were obtained by George von Békésy in cadavers using intense click stimuli [Fig. 11 of von Békésy (1949a)]. The corresponding signal-front delays, shown in Fig. 5 (filled squares), are very similar to those in living chinchillas (dashed line) over the entire apical half of the cochlea and probably in the basal half as well, considering that both sets of data approach a 0-ms asymptote at high CFs. Figure 5 also shows the BF group delays of postmortem BM responses in the cochleae of humans (filled symbols) and experimental animals. Again, for any particular BF region, postmortem BF group delays are similar in all species, including humans.

FIG. 5.

Postmortem BM signal-front and BF group delays in the cochleae of humans and other mammals. Delays are expressed in milliseconds. Dashed lines, in vivo signal-front delays in chinchilla. Solid lines, the trend of postmortem BF group delays in all species. Signal-front delays in the cochleae of human cadavers from Figure 11 of von Békésy (1949a). Best frequency group delays in the cochleae of human cadavers: from Figures 4 and 5 of von Békésy (1947), Figure 5B of Stenfelt et al. (2003), and Figure 3 of Gundersen et al. (1978). Postmortem delays in chinchilla: Figure 1 of Ruggero et al. (2000), Figure 10 of Recio et al. (1998), Figure 7 of Cooper and Rhode (1996), Figures 1A and 2D of Rhode and Recio (2000), and Figure 4 of Ruggero et al. (1992). Guinea pig: from Figure 6 of Zinn et al. (2000) and Figure 6 of Nuttall and Dolan (1996). Gerbil: from Figure 3 of Ren and Nuttall (2001) and Figures 4 and 5 of Overstreet et al. (2002a). Squirrel monkey: from Figures 2, 3, and 4 of Rhode (1973).

The effects of death on BM group delays

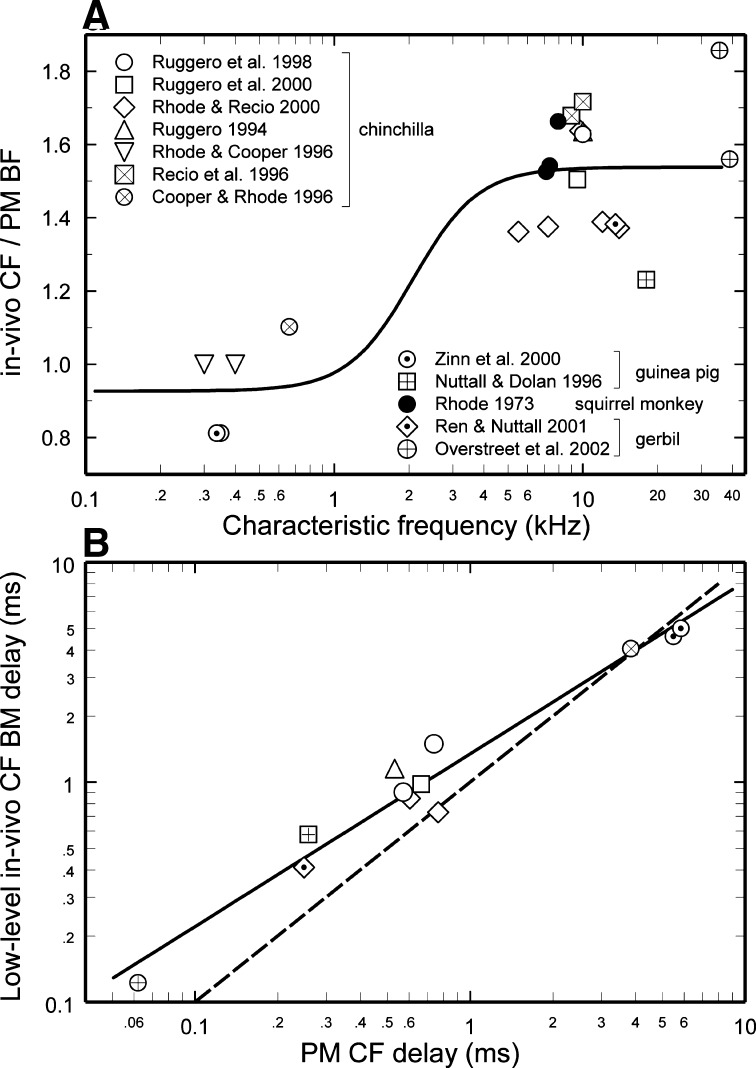
To estimate in vivo CF group delays in humans from postmortem data, it is necessary to compensate for postmortem effects [reviewed in p. 1336 of Robles and Ruggero (2001)]. Figure 6A summarizes, for experimental animals, the effects on BF of death or, equivalently in vivo, of raising the stimulus level from low (i.e., the levels at which CF is measured) to high. Data points are included only when in vivo responses to low-level stimuli were measured in reasonably healthy cochleae. Specifically, Figure 6A shows in vivo CFs as a fraction of the postmortem BFs (or of the BFs of responses to intense stimuli). At the apex of the cochlea, postmortem BFs are nearly the same as (in vivo) CFs. At the base of the cochlea, CFs are 120–190% of postmortem BFs (mean ∼150%). In other words, at the base of the cochlea, postmortem BFs are shifted downward by about 0.5 octave relative to in vivo CFs.

FIG. 6.

In-vivo CFs and CF group delays for low-level stimuli in mammalian cochleae expressed as ratios of postmortem BFs and postmortem CF group delays. A In vivo CFs expressed relative to the BFs of responses to intense stimuli postmortem (plain symbols) or in vivo (dotted symbols). B The relationship between in vivo CF BM group delay for low-level stimuli and postmortem CF group delay in experimental animals. Solid line, trend between in vivo CF group delay for responses to low-level stimuli and postmortem CF group delay. Dashed line, equality between in vivo CF group delay for low-level stimulation and postmortem CF group delay. Chinchilla: from Figures 11A and B of Rhode and Cooper (1996), Figure 5 of Cooper and Rhode (1996), Figure 9 of Ruggero et al. (1997), Figure 1 of Ruggero et al. (2000), Figures 1C, 2B, 3B, and E of Rhode and Recio (2000), Figure 10 of Recio et al. (1998), and Figures 2 and 4 of Ruggero et al. (1992). Guinea pig: from Figure 6 and Table I of Zinn et al. (2000) and Figure 6 of Nuttall and Dolan (1996). Gerbil: from Figure 3 of Ren and Nuttall (2001) and Figures 4 and 5 of Overstreet et al. (2002a).

Figure 6B summarizes the effects of death on the slopes of phase-vs.-frequency curves for most of the measurements represented in Figure 6A. [Squirrel monkey data are not included because they are available only for cochleae exhibiting signs of deterioration.] Such effects consist of the abolition of the intensity dependence of group delay, which is longest for in vivo response to low-level stimuli and shortest for intense stimulation either in vivo or postmortem [Fig. 4B and pp. 1311–1312 of Robles and Ruggero (2001)]. For reference, Figure 6B includes a dashed line indicating equality between postmortem CF delay and in vivo CF delay for low-level stimulation; i.e., the line indicates a lack of dependence of CF phases on intensity, as would be the case for (hypothetical) linear responses. The effects of death (or, in vivo, of stimulus intensity) are seen in Figure 6B as a divergence between the dashed line and the actual trend of in vivo CF delay as a function of postmortem CF delay (solid line).

Figure 7 shows the signal-front delays for living humans (open symbols) and chinchillas (thin dashed line), reproduced directly from Figure 5 (because they are not affected by death) and plotted at CFs corrected according to Figure 4A. The signal-front delays are similar in the two species. The trends of Figure 6A and B for experimental animals were used to derive in vivo CF group delays in humans (filled symbols in Fig. 7) on the basis of postmortem BF group delays in humans (Fig. 4A). First, the postmortem BFs were translated into in vivo CFs according to the trend line of Figure 6A. Then, the postmortem CF group delays (taken as identical to the postmortem CF group delays because of the near linearity of the phase-vs.-frequency curves for humans) were translated into in vivo CF group delays for low-level stimuli according to the trend line of Figure 6B. The derivation of in vivo CF group delays from postmortem BM group delay data is based on the assumption that the quantitative relationship between postmortem and in vivo CF delays is approximately the same across all mammalian species and therefore is also applicable to humans. (The “Discussion” section presents evidence that the applicability to human cochleae of the quantitative relationship between postmortem and in vivo delays in the cochleae of experimental animals is not an arbitrary assumption but rather is founded on strong experimental evidence.)

Figure 7 also shows the trend (thin solid line) of in vivo CF group delays for low-level stimulation in chinchilla (Temchin et al. 2005). The in vivo CF group delays for humans and chinchillas are similar throughout most of the range of CFs. This similarity is of interest because the two species have comparable auditory thresholds and nearly identical hearing ranges [so that their cochlear maps are scaled versions of each other (Greenwood 1990)], but their BM lengths differ by a factor of nearly two (chinchillas, 18 mm; humans, 35 mm). The similarity of delays in spite of widely different BM lengths contradicts the conjecture that “the absolute magnitude of wave velocity in live human cochleae is roughly the same (as in others mammals)” [page 227 of Zwislocki (2002)] and its corollary, that because “human subjects have longer...cochleas” they must have “longer cochlear travel times than most experimental animals” [pp. 655–656 of Neely et al. (1988)]. [Caveat: Zwislocki’s conjecture was based on an analysis of phase delay, a measure that can differ substantially from CF group delay (see Fig. 1).]

The minimal (or absent) dependence of BM delays on BM length is further illustrated in Figure 8, which shows that the signal-front (Fig. 8A) and CF group delays (Fig. 8B) of human cochleae are similar to the corresponding delays in the cochleae of other mammals (cat, guinea pig, and squirrel monkey, as well as chinchilla) with shorter BMs.

Similarity of CF group delays among mammalian and nonmammalian tetrapods

Signal-front and CF BM group delays in human cochleae (Fig. 8) are also similar to delays in the extremely short hearing organs of nonmammalian tetrapods [see Fig. 6B of Ruggero and Temchin (2005)]. Such similarity is remarkable in the case of the bobtail lizard Tiliqua, whose BM does not support a traveling wave (Manley et al. 1988), and even more remarkable in the case of frogs (Hillery and Narins 1984; Hillery and Narins 1987), whose hearing organs lack BMs altogether. The implication is that systematic increases of signal-front and/or CF group delay as a function of decreasing CF do not necessarily reflect BM waves that travel from base to apex (Köppl 1997b; Manley 1990; Smolders and Klinke 1986).

DISCUSSION

Justification of the assumption that the effects of death on cochlear amplification and group delays in humans can be derived from the corresponding effects in experimental animals

The general assumption underlying the derivation of in vivo CF group delays from data in experimental animals is that cochlear processes in humans are similar to those in other mammalian species. Here we present evidence that the applicability to humans of quantitative relationships derived from experimental animals is not a mere assumption but rather a reasonable hypothesis supported by many facts. Specifically, we show below that (1) in vivo CFs and postmortem BFs are quantitatively related to each other in the same manner as they are in experimental species (Fig. 6A) and (2) in vivo CF group delays and postmortem CF group delays are quantitatively related to each other in the same manner as they are in experimental species (Fig. 6B).

Hypothesis 1 is supported by the phenomenon of “the half-octave shift”: temporary threshold shifts induced by exposure to intense tones in humans (Davis et al. 1950) and other animals (Cody and Johnstone 1980) cause the greatest hearing-threshold elevations at frequencies one-half octave higher than that of the intense tone. It is almost certain that the half-octave shift reflects a corresponding shift in BM BF following death (Sellick et al. 1982) or stimulation with intense stimuli (Ruggero et al. 1996).

Hypothesis 2 is supported by the following facts.

1. Postmortem, the peak gains of BM motion (i.e., at BF) relative to incus or stapes motion are similar in humans and in experimental animals [humans, 10–25 dB, Figs. 2 of Gundersen et al. (1978) and 5A of Stenfelt et al. (2003); squirrel monkey, 7–15 dB, Fig. 9 of Rhode (1978); gerbil, 26 dB, Fig. 6 of Overstreet et al. (2002a); and chinchilla, 20 dB, Fig. 5 of Recio and Rhode (2000)].

2. The peak magnitude of stapes or incus velocity gain (re stimulus pressure) is similar (in the order of 0.3 mm s⁻¹ Pa⁻¹) in humans and in experimental species [humans, Fig. 3 of Aibara et al. (2001); squirrel monkey, Figs. 3 and 4 of Rhode (1971); gerbil, Fig. 2 of Overstreet and Ruggero (2002); chinchilla, Fig. 1 of Ruggero et al. (2007)].

3. “...Most mammals, including humans, have the lowest (auditory) thresholds within 10 dB of 0 dB SPL” [pp. 7–8 of Fay (1994)]. In other words, with few exceptions, “the lowest level of stimuli that can be detected within the BF range is approximately the same for all mammalian species” [pp. 24–25 of Long (1994)].

4. Postmortem changes in CF group delay are almost nil for low-CF sites (Cooper and Rhode 1996; Zinn et al. 2000).

5. For high-CF sites, CF group delays are shortest postmortem or, in vivo, for intense stimuli; in vivo, CF group delays become systematically longer as stimulus levels are decreased or when cochlear health deteriorates [e.g., Fig. 2 of Ruggero (1994); reviewed on p. 1336 of Robles and Ruggero (2001)]. However, when CF group delay changes do occur postmortem, they are relatively small; e.g., 0.38 ms at the 10-kHz site of chinchilla (Ruggero et al. 1997) or 0.25 ms at the 18-kHz site of guinea pig (Nuttall and Dolan 1996), corresponding to in vivo re postmortem gains at CF (i.e., “amplification”) of 65 and 60 dB, respectively. The ratio of postmortem group delay change to the corresponding gain change indicates the rate at which CF group delay varies with amplification: 5.8 μs/dB for chinchilla and 4.2 μs/dB for guinea pig.

From a, b, and c, it follows that the strength of cochlear amplification (the amount by which in vivo sensitivity exceeds postmortem sensitivity at CF) must be approximately the same in humans and other species. According to d, postmortem and in vivo CF group delay are the same for low CF regions in experimental animals and, hence, also probably in humans. According to e, even if large differences exist between humans and other species in the strength of cochlear amplification, those differences would be accompanied by relatively minor differences in CF group delay. For example, if amplification at CF were to amount in humans to 100 dB (i.e., 40 dB or two orders of magnitude higher than in chinchilla or guinea pig), the equation illustrated in Figure 6B would underestimate by only 160–240 μs (i.e., 40 dB times 4.2 or 5.8 μs/dB) the CF group delays for CFs of 10–18 kHz.

Comparability of postmortem measurements of BM vibration in humans and in experimental animals

A matter of concern in extending observations in experimental animals to humans is whether the respective functional and structural properties are validly comparable. Postmortem observations in animal experiments (such as illustrated in Figs. 4–6) are typically carried out soon (within minutes or a few hours) after death, when cochlear structures may be presumed to remain largely intact. In contrast, BM vibration measurements in human temporal bones appear to have been carried out, at the earliest, several hours after death. Von Békésy stated that his vibration measurements were made in “fresh” temporal-bone preparations (von Békésy 1949b), but such explicit statements are lacking in von Békésy (1947) and von Békésy (1949a). The latter papers, however, refer to the use of “fresh” preparations in other contexts. Gundersen et al. (1978) gave no details regarding their temporal bone preparations, but another publication reporting on the same experiments states that measurements were carried in “temporal bones...prepared 8–24 h postmortem” (Kringlebotn et al. 1979). Stenfelt et al. (2003) made their BM measurements within 6 days after death in temporal bones that had been extracted 2 days after death and stored at 5°C in a 1:10,000 merthiolate solution in normal saline (Stenfelt et al. 2003).

The concern about the dissimilarity of cochlear conditions in human temporal bones and in experimental animals is somewhat allayed by the fact that most postmortem changes in BM responses in experimental animals, in particular the disappearance of nonlinear features (including the dependence of CF group delay on stimulus intensity; Fig. 6B), occur soon (within minutes) after death (Recio et al. 1998; Rhode 1973). Nevertheless, lingering changes in “passive” features were noted by Kohllöffel (1972) and Rhode (1973). Of special interest is that, after the initial postmortem effects (Fig. 5B), further changes (decreases) in near-CF group delays remained small for as long as 31 h in squirrel monkey [see Fig. 4 of Rhode (1973)]. Kohllöffel compared responses in guinea pig cochleae 4 and 7 days after death and found that there was “practically no effect of aging on the phase patterns” (Kohllöffel 1972).

Significance of the present findings for the concept of a traveling wave

In a 1954 paper, Wever, Lawrence, and von Békésy reconciled some of their views on the nature of the traveling wave. They stated that when the cochlea is stimulated with a tone, a BM “displacement wave seems to be moving up the cochlea. Actually...each element of the membrane is executing sinusoidal vibrations...different elements...executing these vibrations in different phases. This action can be referred to as that of a traveling wave, provided that...nothing is implied about the underlying causes. It is in this sense that Békésy used the term ‘traveling wave’...” [pp. 511–513 of Wever et al. (1954)]. More than half a century later, the nature of cochlear mechanical “traveling waves” remains a matter of argument, as demonstrated by a recent discussion in Portland, OR [see pp. 534–539 of Nuttall et al. (2006)]. Nevertheless, we agree with many others that physical traveling waves propagate in the mammalian cochlea, carrying energy from base to apex. Such traveling waves apparently result from interactions between fluid inertia and the structural properties of the organ of Corti and the BM, principally the latter’s elasticity. The evidence for the existence of traveling waves in mammalian cochleae is abundant [see reviews by Robles and Ruggero (2001) and Ruggero (1994)]. Numerous measurements of BM vibration [especially those of Russell and Nilsen (1997), Ren (2002), and Rhode and Recio (2000)], of fluid pressure in scala tympani near the BM (Olson 1998) and of responses of auditory nerve fibers (Pfeiffer and Kim 1975) have been complemented and interpreted by substantial theoretical and/or modeling work on hydrodynamics (de Boer 1984; Lighthill 1981; Mammano and Nobili 1993; Peterson and Bogert 1950; Taber and Steele 1981; Zwislocki 1948).

The situation is less clear in nonmammalian hearing organs. In particular, substantial signal-front delays that increase from high-CF to low-CF regions (Fig. 8) exist in the hearing organs of the bobtail lizard (Tiliqua), in which the BM does not sustain a traveling wave (Manley 1990), and frogs, which lack BMs altogether. Obviously, the concept of the traveling wave cannot be applied to those hearing organs in the same sense that it applies to mammals (Robles and Ruggero 2001; Ruggero 1994). Nevertheless, mechanical traveling waves may well be sustained by structures other than BMs, such as the tectorial membrane in the amphibian papilla of frogs (Hillery and Narins 1984) and the tympanic membrane of locusts (Windmill et al. 2005).

SUMMARY AND CONCLUSIONS

Assertions based on SFOAEs and BSERs that BM delays are much longer in humans than in experimental animals, as well as estimates of BM delays based on DPOAEs, are probably invalid because they depend on assumptions that are invalid for experimental animals. The validity of derived-band estimates of BM delays in humans is uncertain. Derived-band delay estimates should be calibrated against BM delays in experimental animals. Signal-front and BF BM group delays in the cochleae of human cadavers are similar to the corresponding postmortem delays in other mammals (Fig. 5). Measurements in experimental animals of the effects of death or, in vivo, of the intensity-dependence of BM responses (Fig. 6), permit the estimation of CF group delays for living humans (Fig. 7) on the basis of BM delays in cadavers (on the assumption that the relationship between postmortem and in vivo delays is similar across species). Signal-front and CF group delays in the cochleae of living humans appear to be similar to the corresponding delays in chinchillas, other mammals, and even nonmammalian species, including those in which a BM traveling wave does not exist (Fig. 8).