An Enquiry into Metabolite Domains

Abstract

It is currently assumed that two or more pools of the same metabolite can coexist in the cytosolic compartment of mammalian cells. These pools are thought to be generated by the differential subcellular location of enzymes and transporters, much in the way calcium microdomains arise by the combined workings of channels, buffers, and pumps. With the aim of estimating the amplitude and spatial dimensions of these metabolite pools, we developed an analytical tool based on Brownian diffusion and the turnover numbers of the proteins involved. The outcome of the analysis is that ATP, glucose, pyruvate, lactate, and glutamate cannot be concentrated at their sources to an extent that would affect their downstream targets. For these metabolites, and others produced by slow enzymes or transporters and present at micromolar concentrations or higher, the cytosol behaves as a well-mixed, homogenous compartment. In contrast, the analysis showed microdomains known to be generated by calcium channels and revealed that calcium and pH nanodomains are to be found in the vicinity of slow enzymes and transporters in the steady state. The analysis can be readily applied to any other molecule, provided knowledge is available about rate of production, average concentration, and diffusion coefficient. Our main conclusion is that the notion of cytosolic compartmentation of metabolites needs reevaluation, as it seems to be in conflict with the underlying physical chemistry.

INTRODUCTION

Membranes provide the chief mechanism of substrate compartmentation in the cell. Their presence allows ions, metabolites, vitamins, and other water-soluble molecules to be segregated, generating pools that reduce or avoid cross talk between metabolic or signaling pathways. However, compartmentation can also exist in the absence of membranes. A well-known example is the dynamic microdomain that forms at the cytosolic mouth of an open calcium channel, which can sustain concentrations several orders-of-magnitude higher than that in the bulk cytosol. A given target located inside one of these domains is much more likely to bind calcium coming through the channel than calcium diffusing from other regions of the cytosol. By allowing spatial segregation of processes that require different calcium concentrations, microdomains are essential for physiological regulation and may participate in disease (1).

This article is concerned with pools of other small molecules that are also deemed to exist in the cytosol, without the benefit of an intervening membrane. For example, the Na⁺/K⁺ ATPase, the Ca²⁺ ATPase, and the H⁺ ATPase are thought to be fed by glycolysis, whereas mitochondria-bound hexokinase is thought to be fed preferentially by oxidative phosphorylation, ideas that imply the existence in the cytosol of separate pools of glycolytic and mitochondrial ATP (2–10). Other examples found in the literature are the pools of pyruvate and lactate that have been proposed to exist in the cytosol of brain astrocytes and the various pools that account for functional separation between glycolysis and gluconeogenesis in hepatocytes (11–15). As none of these metabolite pools has been measured directly, their characteristics remain obscure. Another pool of interest, which has, in fact, been detected with a probe, is the subplasmalemmal ATP microdomain of β-cells, a putative piece in the machinery of glucose sensing by the pancreas (16).

Our aim here was to investigate these metabolite compartments, by developing a mathematical model of diffusion in the steady state.

THEORY

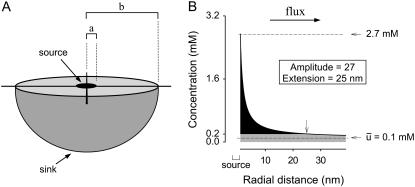
Our model of diffusion in the cell considers two concentric spheres (Fig. 1 A). The surface of the inner sphere, with radius a, is the source of molecules that are evacuated through the surface of the outer sphere of radius b. In the region bounded by the spheres, molecules are assumed to diffuse after Brownian motion. In this way, the concentration u(r, t), at the point r, in a time t, is given by the standard diffusion equation

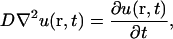(1)

where D is the diffusion coefficient. We are interested in the steady-state regime, where concentration does not change. In this case, the concentration is fixed by the Laplace equation

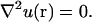FIGURE 1.

Geometry of the model and definition of parameters. (A) A mammalian cell is pictured as a sphere of radius b. A metabolite is produced by a single source of radius a, located at the center of the cell, and diffuses freely, to be cleared at the cell surface (sink). (B) A metabolite domain generated in the steady state. The concentration along the radius of the cell was calculated using Eq. 4. In this example, the concentration at the source was 2.7 mM and the average was 0.1 mM, Amplitude was therefore 27. At 25 nm from the source (arrow), a distance that is referred to as the domain Extension, the concentration falls to below a value equivalent to twice the cell average.

Considering the geometry of the model, it is natural to use spherical coordinates and to assume that the concentration is isotropic and only depends on the radial distance r. Thus, the Laplace equation takes the form

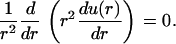(2)

We choose the boundary conditions

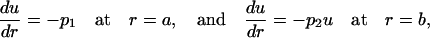(3)

where p₁ and p₂ are constants that will be related with the experimental data below. The boundary condition on the interior surface, r = a, fixes a constant flux through this surface, which acts like a source, and the boundary condition at the exterior surface, r = b, allows a flux proportional to the concentration. The second-order Eq. 2 is easily solved, and the two integration constants appearing in the general solution are determined using the boundary conditions, yielding the expression for the concentration

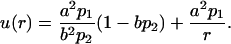(4)

Note that the relation 4πa²du/dr|_r=a = 4πb²du/dr|_r=b is verified by the concentration curve given by Eq. 4, which means that the flux of the particles is conserved. This fact is expected in a steady-state regime.

An observable quantity is the average concentration. Its value is given by

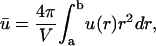(5)

where V = 4π(b³ − a³)/3 is the volume enclosed between the two spheres. Replacing Eq. 4 in 5 yields

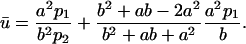(6)

Another measurable quantity is the flux q (molecules/s) through the outer surface,

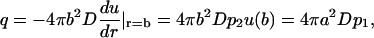(7)

where the last equality is obtained using the particles flux conservation.

Equations 6 and 7 allow expression of the parameters p₁ and p₂ in terms of the experimental parameters :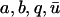

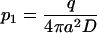(8)

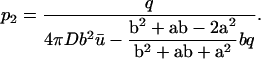(9)

To illustrate the strength of a domain it is useful to determine the ratio between the concentration at the source, u(a) and the average concentration ū in the cell. We termed this ratio, Amplitude:

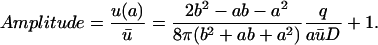(10)

Note that if b ≫ a,

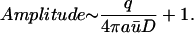(11)

To quantify the size of a domain we define the parameter Extension as the value of the radial coordinate at which the concentration is twice the average:

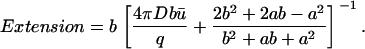(12)

If b ≫ a,

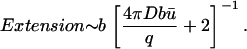(13)

A more general model

In some cases, the sink is not located at the cell surface, but somewhere in between the source and the surface. To account for this possibility we have now dissociated the sink (at r = b) from the cell radius, which will be termed c. Since there is no sink other than at r = b, in the region r ≥ b the concentration must be constant and given by u₀ = u(b). Thus the average concentration is

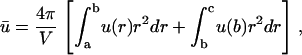(14)

where V = 4π(c³ − a³)/3 is the volume enclosed by the two spheres. Replacing Eq. 4 in Eq. 14 yields

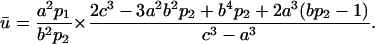(15)

In this case,

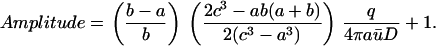(16)

Note that the two factors within parenthesis are <1, hence

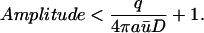(17)

Thus, there is an upper bound for the Amplitude, which is independent of b and c.

For this case, the Extension is given by

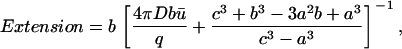(18)

and if c ≫ a, we have

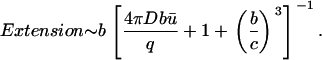(19)

RESULTS

The general case of a single source was first considered, for example, an enzyme or a transporter situated in the center of a spherical cell and producing at a constant rate. The sink is considered to be distributed homogenously at the plasma membrane. In between source and sink, an isotropic medium, the cytosol, allows Brownian diffusion of the metabolite (Fig. 1 A). For this ideal system, solved analytically in the steady state, local concentration can be calculated provided there is prior knowledge of six quantities: flux; diffusion coefficient; average concentration; distance from the source; size of source; and size of sink (Eq. 4). According to the spherical geometry of the compartment, concentration is observed to decay with the inverse of the distance from the source, the gradient being small or large depending on the relative value of the parameters. If the gradient is large, there is a region around the source where the concentration is much higher than average, thus a local domain, pool, or compartment is said to exist. If the gradient is small, no domain is observed. In this model, all the molecules present in the compartment come from the same source, which is obviously not what happens in a cell. However, provided that the average concentration is the same, the behavior will be identical to that of a system in which there are other sources and a commensurately stronger sink. Whether the bulk is generated by the single central source or there is contribution from other parallel sources, the domain remains the same.

A domain can be described by its strength and by its physical extension. As a parameter of strength, we adopted the ratio between metabolite concentration at the source and the average concentration in the compartment, and termed it Amplitude. Theoretically, the value of this parameter may range from 1 in a perfectly homogenous compartment where there is no flux, to a value of infinity for the strongest domain. To describe the size of the domain, an arbitrary parameter termed Extension was defined as the distance between source and the point at which the concentration falls below twice the compartment average. For example, in the hypothetical cell illustrated in Fig. 1 B, average concentration is 0.1 mM and the maximum at the source is 2.7 mM, which gives an Amplitude of 27. The Extension is 25 nm, meaning that a given target located closer than 25 nm from the source will be exposed to a substrate concentration of at least 0.2 mM. If instead of being at the surface, the sink were located inside, the Amplitude of the domain will decrease (see Eqs. 16 and 17), an effect that becomes significant only when the sink is a few nanometers from the source. For the sake of the argument to follow, it can be safely stated that an internal sink will not increase the Amplitude of a domain. The same line of reasoning can be used to argue that an eccentric source will behave very much like a central source, unless the sink is nanometers away. The Extension, however, is much more sensitive to the presence of an internal sink (Eq. 19). In summary, an internal sink makes the domain sharper but in most cases does not affect its strength.

A glycolytic ATP pool?

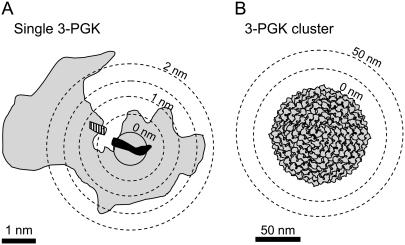
To investigate glycolytic ATP domains, we considered 3-phosphoglycerate kinase (3-PGK, EC 2.7.2.3)—which, with a turnover number of 1000 s⁻¹, is the fastest of the two glycolytic enzymes that produce ATP (BRENDA database, University of Cologne, Germany). The diameter of the source was set at 1 nm, approximately the length of an ATP molecule (Fig. 2 A). With this source size, an average ATP concentration of 5 mM and an effective diffusion coefficient of 500 μm²/s in the cytosol (17), the calculated value of the parameter Amplitude was 1.0001, equivalent to 5.0005 mM. Thus, at the very site of ATP release, the steady-state ATP concentration is only 0.5 μM higher than in the bulk cytosol, meaning that an individual Na⁺/K⁺ ATPase, most favorably located at the ATP release site of 3-PGK, would still get 99.99% of its ATP from other sources. At a more realistic distance of 2 nm, which makes some allowance for the large hinge-bending conformational change that characterizes 3-PGK (18, 19), the ATP concentration drops to a mere 0.1 μM above average. Pyruvate kinase and the adenylate translocase, the other steady-state sources of ATP in the cell cytosol, have smaller turnover numbers and so they fail by a wider margin (Table 1).

FIGURE 2.

3-PGK as a source of ATP. (A) The three-dimensional crystal structure of yeast 3-PGK is outlined in shading, together with the projection of its products Mg-ATP (solid) and 3-phosphoglycerate (hatched), modified from Watson et al. (18). Note that the bulky structure of the enzyme provides a lower limit for the size of the ATP source. (B) A hypothetical cluster of all 3-PGK copies contained in an astrocyte would occupy a sphere of ∼100 nm diameter. The lack of domain generation by either arrangement is discussed in the text.

TABLE 1.

Quantification of some local domains in a typical mammalian cell

Molecule	Diffusion coefficient (D; μm2/s)	Average concentration (ū; mM)	Source	Turnover number (q; s−1)	Amplitude (fold)	Extension (μm)
ATP	500*	5	3-PGK	1000†	1.0001	0
			PK	154†	1.00002	0
			ANT	65‡	1.000007	0
Glucose	500§	1¶	GLUT1	187¶	1.00002	0
Pyruvate	130‖	0.1**	PK	154†	1.003	0
			LDH	269†	1.005	0
			GPT	480†	1.01	0
Lactate	130‖	1.25**	LDH	269†	1.0004	0
			MCT	2000††	1.004	0
Glutamate	210‡‡	1.2**	Glutamate dehydrogenase	130†	1.0001
			GOT	187†	1.0002	0
			GPT	480†	1.0006	0
			Glutaminase	5080†	1.006	0
			Na+-glutamate cotransporter	20§§	1.00002	0
Ca2+	13¶¶	10−4	L-type Ca2+ channel	105‖‖	104 (1 mM)	3.3
			Na+/Ca2+ exchanger	5000***	103 (50 μM)	0.45
H+	37.8†††	4 × 10−5	Cytochrome oxidase	500†	90 (pH 5.4)	0.043
			Ca2+ ATPase	149†	28 (pH 6.0)	0.013
Na+	1160‡‡‡	10	AMPAR	107§§§	1.2	0
			Na+/Ca2+ exchanger	5000***	1.0001	0

Domains were estimated assuming a source radius a of 0.5 nm and a cell radius b of 5 μm, with the sink located at the cell surface. 3-PGK, 3-phosphoglycerate kinase (EC 2.7.2.3); PK, pyruvate kinase (EC 2.7.1.40); ANT, adenine nucleotide translocase; GLUT1, glucose transporter isoform 1; LDH. lactate dehydrogenase (EC 1.1.1.27); GPT, glutamate pyruvate transaminase (EC 2.6.1.2); MCT, proton-coupled monocarboxylate transporter; Glutamate dehydrogenase (EC 1.4.1.3); GOT, glutamate oxalacetate transaminase (EC 2.6.1.1); Glutaminase (EC 3.5.1.2); AMPAR; AMPA type ionotropic glutamate receptor; cytochrome oxidase (EC 1.9.3.1); and Ca²⁺ ATPase (EC 3.6.3.8).

^*de Graaf et al. (17).

^†BRENDA Database, University of Cologne, Germany. The highest turnover numbers measured for mammalian enzymes are given.

^‡Forman and Wilson (27).

^§Vega et al. (22).

^¶Barros et al. (20).

^‖Pfeuffer et al. (23).

^**Hawkins et al. (25); the value for glutamate corresponds to glial cells.

^††The turnover number for MCT was assumed similar to that of the Na⁺/H⁺ exchanger.

^‡‡Valette et al. (24).

^§§Wadiche et al. (28).

^¶¶Allbritton et al. (29).

^‖‖Guia et al. (30).

^***Shigekawa and Iwamoto (31).

^†††Vaughan-Jones et al. (32).

^‡‡‡Goodman et al. (33).

^§§§Smith et al. (34).

A more favorable configuration for domain-building would have many sources in close proximity. At the limit, all copies of 3-PGK would sit in a single cluster, as pictured in Fig. 2 B. To make it even more favorable, we chose brain astrocytes, where glycolysis is fast. A brain glucose consumption rate of 6.5 μM/s (20), which in a 20 μm astrocyte translates to a 3-PGK production rate of 3.3 × 10⁷ ATP molecules per second, will demand the involvement of 3.3 × 10⁴ copies that cycle at 1000 s⁻¹. With a 3-PGK molecular volume of 100 nm³, this cluster will be maximally packed in a sphere of ∼100 nm diameter. After locating such a sphere in the center of the cell and solving the model, the calculated Amplitude value was 1.034, i.e., the ATP concentration on the surface of the cluster is only 3.4% higher than in the bulk cytosol, which is more than that produced by the single enzyme, but still fails to qualify as a domain. The same conclusion applies to a mitochondrion 200 nm in diameter, with a 1:500 share of the astrocytic ATP turnover of 5.6 × 10⁸ per second, where the Amplitude value is 1.001, a modest 0.1% higher than average. A possible “negative” domain, at the site of the Na⁺/K⁺ ATPase, for example, can also be ruled out, for its turnover number is only in the order of 10² s⁻¹.

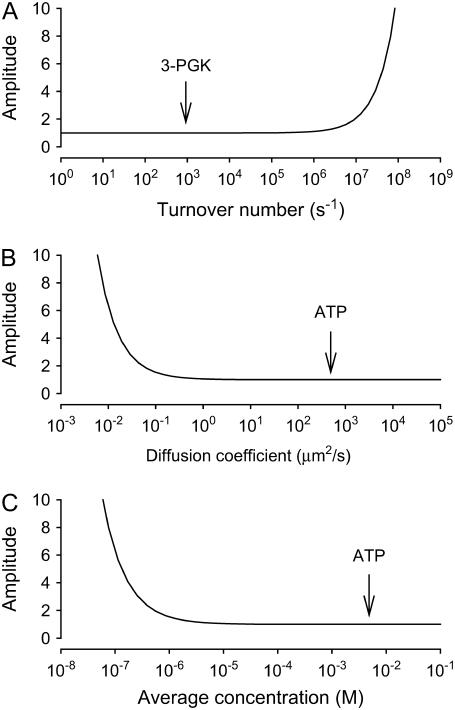
The theoretical conditions that may generate a local ATP domain were further explored using Eq. 10. As illustrated in Fig. 3, for a given source size and cell size, domains will be generated only for extreme values of flux, diffusion coefficient, or average concentration. Out of these three inputs, the only one subject to a degree of uncertainty is the local effective diffusion coefficient. Diffusion may in fact be retarded by tortuosity or by changes in water structure; however, these effects are typically in the order of twofold, well short of the five orders of magnitude that are needed (Fig. 3 B). Incidentally, the requirements for strong ATP domains are met in the extracellular space, where average ATP is low and a single channel can transport ATP at rates in excess of 10⁵ molecules per second (21). In conclusion, even under the most favorable conditions that are compatible with the known physical constraints, ATP pools will not be appear in the cytosol of a compact cell.

FIGURE 3.

Unrealistic conditions are needed to form ATP domains. Domain Amplitude was estimated using Eq. 10 for a source of 1 nm diameter in a cell of 10 μm diameter. (A) After fixing the diffusion coefficient D at 500 μm²/s and the average concentration ū at 5 mM, Amplitude was determined at increasing turnover numbers (q). The arrow points to the place in the curve where 3-PGK is located. (B) With a ū of 5 mM and a turnover number (q) of 1000 s⁻¹, Amplitude was determined at increasing values of D. The arrow indicates the position of ATP, given by its measured value of D in cytosol. (C) Amplitude was calculated at increasing values of ū, fixing D at 500 μm²/s and q at 1000 s⁻¹. Note that five orders of magnitude separate the physiological condition from that required by a domain.

Glucose, pyruvate, lactate, and glutamate pools?

Table 1 includes the parameters that were used to model possible domains of these four metabolites, for which cytosolic pools have been hypothesized. The enzymes or transporters that produce glucose, pyruvate, lactate, and glutamate, cycle at rates similar to that described for ATP synthesis. In vivo diffusion coefficients are available for glucose, lactate, and glutamate (22–24). We could not find a reported estimate of the diffusion coefficient for pyruvate in vivo, so we used the value for lactate, a molecule of similar structure. The concentrations of the four metabolites in the brain are known (20,25). Glucose, lactate, and glutamate are present at mM levels, and thus their calculated Amplitude values were similar to that of ATP (Table 1). Pyruvate, present at a lower concentration, resulted slightly more favorable for domain-building, but still several orders of magnitude away from an Amplitude value of biochemical interest. In conclusion, as for ATP, no significant intracytosolic compartments are to be found for these metabolites either.

Ion domains

As a counterexample we modeled domains generated by ion channels. For the L-type Ca²⁺ channel, the three parameters that determine local gradients are greatly favorable with respect to those for metabolites: flux is three orders-of-magnitude larger, average concentration in the compartment is five orders-of-magnitude lower and diffusion coefficient is one order of magnitude smaller. Their combination amounts to an advantage of nine orders of magnitude with respect to metabolite domains! Thus, a calcium channel has the power to generate a strong spatial domain (Table 1). As calcium is also taken up by intracellular sinks like mitochondria and the endoplasmic reticulum, a calcium domain may be better described with the general model (Eqs. 16–18). For Amplitude, as mentioned above, the results are not significantly different. A sink as close as 50 nm away from the L-type Ca²⁺ channel decreases Amplitude by only 1%. The Extension, however, is much more sensitive, decreasing from 3.3 μm to 25 nm. Even for a much slower Ca²⁺ source like the reverse Na⁺/Ca²⁺ exchanger, a domain peaking 100 μM is expected (Table 1). According to the analysis, acidic domains should be found near mitochondrial cytochrome oxidase and the Ca²⁺ ATPase, which release H⁺ at relatively small rates. For the cytochrome oxidase, the local domain would be further enhanced by restricted diffusion of H⁺ across the outer mitochondrial membrane. For Na⁺ the situation is different. Despite the high conductance of sodium channels, which pass 10⁷ ions per second, domains fail to arise because average intracellular sodium is high, as is its diffusion coefficient (Table 1).

DISCUSSION

The concentration of a given metabolite is highest at the site of its production, thus in principle every enzyme builds up a local domain. However, to be of biochemical consequence, the domain must stand out sufficiently, so that a downstream target can distinguish it from the bulk. Here we have introduced a straightforward analytical tool, which was applied to assess the size and strength of several metabolite pools of possible biochemical relevance. With this tool, molecule pools in any compartment can easily be explored, provided that information is available about rates of production, average concentrations and diffusion coefficients.

The model considers an ideal geometry, so the question arises as to whether it might valid for cells that are not spherical. For example, astrocytes have numerous filopodia-like processes, thin prolongations that extend up to 30 μm away from the soma. By considering a one-dimensional model, it can be demonstrated that diffusion along thin structures like filopodia is not critically different from diffusion in a sphere. Although the concentration profile becomes linear instead of curved, which makes domains broader, the Amplitude is not affected. As for a sphere, bringing the sink closer to the source will make the domain sharper and weaker. However, if the processes were much longer, as in neurons, the mixing effect of diffusion will become negligible; if, in addition, the sink is distributed along the processes, strong domains will be generated. A detailed analysis of neuronal domains will be reported elsewhere.

The data obtained for ATP, glucose, pyruvate, lactate, and glutamate demonstrate that domains/pools do not exist in the cytosol of compact cells, such as astrocytes, hepatocytes, epithelial cells, leukocytes, erythrocytes, etc. For these molecules, the cytosol is a well mixed compartment and no target is preferentially fed by a particular source. This does not necessarily imply that the cytosol is homogenous, for local variations in surface potential may affect slightly the local concentration of charged metabolites. However, such heterogeneity would not be source-specific. The main factors that preclude domain formation in the case of metabolites were found to be the slow rate of production by enzymes and transporters and the high rate of diffusion, the latter explained by the combined effects of high average concentrations and high diffusion coefficients. Metabolite domains fail to materialize because many more molecules are likely to arrive to the source from the bulk than from the source itself. The estimations included in Table 1 were based on average concentrations. The impact of possible concentration changes, either physiological or pathological, can be assessed by examining Eq. 11. For strong domains, the Amplitude will change in inverse proportion to concentration. For example, if average H⁺ concentration is halved, the Amplitude of the domain generated by cytochrome oxidase will double from 90 to 180. In contrast, for weak domains the impact of concentration change is negligible. For example, after halving the ATP concentration, the Amplitude of the domain generated by 3-PGK will barely rise from 1.0001 to 1.0002.

The analysis was validated by its ability to predict the microdomains that have been measured near Ca²⁺ channels. We have assumed a steady state, which though reasonable for slow metabolic processes, may not be applicable to a channel, where flux is far from constant. In this case the assumption of a steady state will underestimate the strength of a transient domain. It is considered that Ca²⁺ microdomains are all transient and do not arise in the steady state (1), but our data suggest that this need not be the case. Standing calcium domains may be instrumental to the regulation of slower physiological processes such as metabolism, cell death, and gene expression (26). Limiting factors to calcium domains in the steady state would be the extrusion capacity of pumps and carriers and the metabolic capacity of the cell to feed the pumps, which may not be able to match a high open probability channel. Another outcome of the analysis is the prediction that even slow transporters and enzymes may have the ability to build up nanodomains of Ca²⁺ and H⁺. This is due to the combination of low concentrations and low diffusion coefficients.

Metabolite domains or biochemical “compartments” are thought to exist in the cytosol of astrocytes, hepatocytes, pancreatic β-cells, erythrocytes, and other cell types. Having shown that the existence of such compartments is unlikely, rather than speculating about specific datasets, we hope to foster the search for alternative explanations. Enzyme channeling, membrane compartmentation of enzymes, pathway segregation between cells (e.g., subtypes of astrocytes), and of course, artifacts, are possibilities that spring to mind. It is well established that enzymes and transporters can be part of macromolecular assemblies, often in the vicinity of their targets. Our contention is that such association does not relate to the building up of local substrate pools.