TABLE 3.
Rules table of CA modeling of regulatory network of mitochondrial apoptosis
| Descriptions of reactions | ||
|---|---|---|
| Act + InBax | 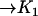 |
Act + AcBax |
| AcBax | 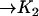 |
InBax |
| AcBax + Bcl2 | 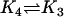 |
AcBaxBcl2 |
| Act + Bcl2 | 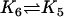 |
ActBcl2 |
| AcBax + ActBcl2 | 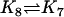 |
Act + AcBaxBcl2 |
| AcBaxm + AcBaxn | 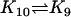 |
AcBax (m+n)* |
| Ena + Bcl2 | 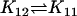 |
EnaBcl2 |
| AcBax + EnaBcl2 | 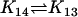 |
Ena + AcBaxBcl2 |
| Ena + ActBcl2 | 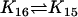 |
Act + EnaBcl2 |
| AcBax + CC | 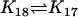 |
AcBaxCC |
| Bcl2 + CC | 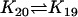 |
Bcl2CC |
| AcBax + Bcl2CC | 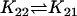 |
AcBaxCC + Bcl2 |
| With | ||
| Rate constants
| ||
| K1 = 200 | K10d = 2 | K17 = 350 |
| K2 = 6 | K10t = 1 | K18 = 1 |
| K3 = 400 | K11 = 500 | K19 = 400 |
| K4 = 2 | K12 = 1 | K20 = 1 |
| K5 = 500 | K13 = 150 | K21 = 10 |
| K6 = 1 | K14 = 150 | K22 = 150 |
| K7 = 250 | K15 = 250 | |
| K8 = 150 | K16 = 15 | |
An AcBax polymer can react with another to produce a lager AcBax polymer. In realistic reaction systems, the rate constants of Bax dimerization, trimerization, etc. must be different. We here make a simple assumption that larger polymers of AcBax are more likely to polymerize and the set of rate constants are defined by K9 = 1000 × (m+n)/(B+(m+n)). Here m, n, and m+n are molecular weights of these polymers; B is a parameter to regulate the relationship between K9 and (m+n). We adopt B = 10 to make the value of K9 comparable to other rate constants used in our CA simulation. Bax dimers and trimers are supposed to be able to dissociate and the dissociation constants are defined as K10d and K10t, respectively. The formation of larger Bax polymers is supposed to be irreversible. The parameters K1 to K9, K10d, and K10t are chosen to preserve the main ratio relationships among them in ODEs modeling. According to this set of parameters, K11 to K22 are chosen in such a way to realize stable dynamics on the simulation grid of our CA model as described by Siehs et al. (20).
