Figure 6.

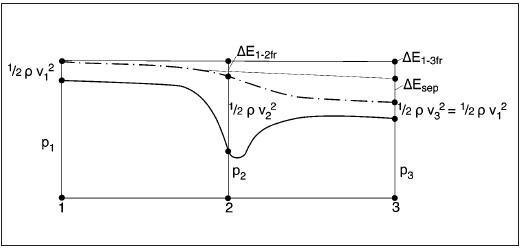
The pressures, velocities and energy losses are related in the energy equation. The basic assumption is that the sum of potential energy (pressure P), kinetic energy (local velocity v) and energy losses (shear stress: ΔE_fr, separation: ΔE_sep) is constant. While v₂ is higher than v₁ and ΔE_1-2fr is relatively small, P₂ is smaller than P₁ (see also figure 3). After the bend the velocity v2 decreases to v₃ (=v₁): the pressure increases but will be lower than p1 because of the energy loss by the eddies of the separation.