Further Analysis of the Matching Law to Describe Two- and Three-point Shot Allocation by Professional Basketball Players

Abstract

The matching law was used to analyze whether the proportion of shots taken from two- or three-point range would match the proportional reinforcement rates produced by those shots when the reinforcement rate of three-point shooting was changed. Rule changes in 1994 and 1997 altered the distance of the three-point line in the National Basketball Association, which created a quasiexperimental reversal design, thereby naturally changing three-point reinforcement rates. The present data partially confirmed predictions made by the matching law, in that increases in the relative rate of three-point shots attempted corresponded to increases in the relative rate of three-point shots made.

The matching law is a mathematical description of the relation between relative response and reinforcement rates first postulated by Herrnstein (1961). The matching law states that relative response rates will match relative reinforcement rates produced by that responding. Vollmer and Bourret (2000) showed that the matching law accurately described seemingly complex human behavior such as the allocation of two- and three-point field goal shooting by both men's and women's college basketball players over the course of an entire season at a Division I school (Vollmer & Bourret). In that study the response alternatives were the number of two- and three-point shots attempted by each player, and the reinforcer that maintained the behavior was the number of points scored contingent on making those shots. The only qualification for a player to exhibit a matching relation was an adequate amount of playing time. Thus, these players allocated shots proportional to the reinforcement obtained from making those shots. In the study by Vollmer and Bourret, however, the reinforcement rates for both two- and three-point shots were not systematically changed. Without a change in reinforcement rates, strong conclusions could not be made as to whether or not relative reinforcement rate was responsible for the observed changes in response rates.

Over the past several years, the three-point shooting distance in professional basketball was first decreased and then subsequently increased after 3 years. The result may have been a change in reinforcer probability and reinforcement rate for three-point shots for some players. For these players, as the three-point line was moved closer, three-point shooting may have been more likely to be reinforced, thus producing a higher rate of reinforcement. When the line was moved back to its original distance, the likelihood of making a three-point shot then decreased. The present study is an attempt to replicate and extend the findings of Vollmer and Bourret (2000) by analyzing this quasiexperimental manipulation. If the relative reinforcement rate for three-point shots increased when the three-point arc was moved closer, a higher relative rate of three-point shots should have been attempted during this time. Conversely, when the three-point arc was moved back further from the basket, relative reinforcement rates should decrease, producing a lower relative rate of three-point shots attempted.

Method

Data were obtained from the official National Basketball Association (NBA) Web site (www.nba.com), from the ESPN Web site (www.espn.com), and from the Official NBA Encyclopedia (3rd ed., Hubbard, 2000) for the 1991–1992 through 1999–2000 NBA regular seasons. Subjects were selected for this study based on the following criteria: (a) The individual had participated in at least half of the possible games in each of the three conditions of the study, (b) the individual had an average of at least three shots attempted per game throughout the 9-year period, (c) the individual had participated in at least one game for each of the nine consecutive seasons under study, and (d) the individual made at least one three-point shot during each 3-year period. A total of 57 players met these criteria.

A reversal A-B-A design naturally occurred over this 9-year period. The A conditions consisted of the three-point arc positioned at 23 ft 9 in. from the top of the key and 22 ft from the baseline. The B condition consisted of the three-point arc positioned at a universal 22-ft distance, both from the top of the key and the baseline (www.nba.com).

Data were plotted as the log ratio of three-point shots attempted divided by two-point shots attempted as a function of the log ratio of three-point shots scored divided by two-point shots scored. Baum (1974) proposed the generalized matching equation to quantify systematic deviations from matching. The generalized matching equation is as follows:

where B and R represent the number of shots attempted and scored, respectively. In the current study, B₁ is the number of three-point shots attempted during a single season, and B₂ is the number of two-point shots attempted for that same season. R₁ represents the number of three-point shots scored during a season, and R₂ is the number of two-point shots scored during that season.

The b term shows bias, and the s term represents sensitivity to relative reinforcement rate (Baum, 1974). A bias in responding describes a preference for one alternative over the other independent of relative reinforcement rate. Thus, on a graph, bias is shown by any deviation of the y intercept away from zero without affecting the slope. In the current study, positive bias would indicate a preference for three-point shots, and a negative bias would indicate a preference for two-point shots. When s is greater than or less than 1.0, this is reflected in changes in the slope of the line, and the results are described in terms of overmatching and undermatching, respectively.

Results and Discussion

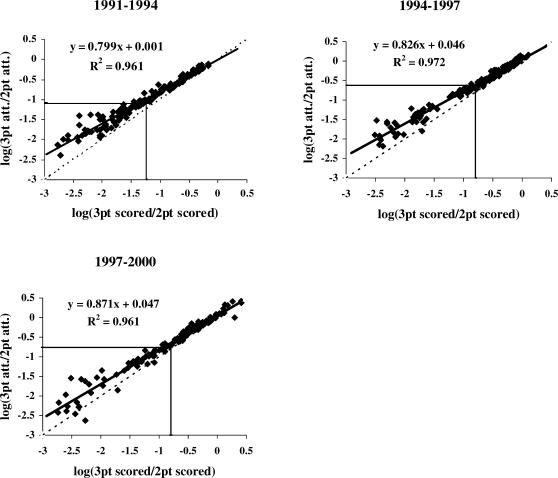
Figure 1 shows the log response ratios plotted against the log reinforcement ratios for the 57 players who met inclusion criteria for the study during each 3-year period. Each point represents data from one season for one player. The dashed diagonal line on each graph represents perfect matching, and the solid line represents the best fit (regression) equation for each 3-year period.

Figure 1.

Log response ratios plotted against log reinforcer ratios for the three different conditions of the study. Data from 57 players who made at least one three-point basket for each 3-year period are included. Each point represents data from one player for one 3-year period. The dashed horizontal lines represent the log of the mean response ratio for all players during each 3-year period. The solid diagonal line is a best fit line for all points. The equation describes the best fit line and displays sensitivity (slope) and bias (y intercept), and the dashed diagonal line represents perfect matching.

The regression lines in Figure 1 illustrate that overall, matching was closely approximated in all three 3-year periods. Comparing the fitted equations from 1991–1994 and 1994–1997 when the three-point line was moved closer to the basket shows a small increase in bias toward the three-point shot (y intercept .001 to .046). This bias toward three-point shooting was maintained after the line was moved back to its original distance during the 1997–2000 seasons (y intercept .047). Unlike those of Vollmer and Bourret (2000), the current data were not calculated with a concatenated version of the matching equation to equate the absolute amount of reinforcement obtained by each response alternative. As shown in their data, equating reinforcement amounts eliminated a bias towards three-point shots. Thus, the slight bias shown for three-point shooting in the current data may be a function of not equalizing reinforcement amounts.

The correlation between responses and reinforcers in all three conditions was accounted for quite well by the fitted equations, as shown in the R² values (between .961 and .972). Undermatching was observed in all three conditions, with the slope of the regression equation less than 1.0.

Within each 3-year period, the mean log relative reinforcement ratios were −1.247, −0.797, and −0.797, respectively. This is represented on Figure 1 as the solid vertical lines on the x axis. The data indicate that moving the three-point line closer increased the mean relative rate of three-point shots made. However, moving the line back did not alter the mean relative rate of three-point shots made in the opposite direction. The mean log relative response rates are represented as the solid horizontal lines on the y axis in Figure 1, and were −1.097, −0.623, and −0.760, respectively, across 3-year periods. Thus, decreasing the three-point distance increased the mean relative rate of three-point shot attempts, and increasing the distance decreased the mean relative rate of three-point shot attempts.

Table 1 provides the mean number of two- and three-point shots attempted and scored, the mean two- and three-point completion percentages, and the mean log reinforcement and response ratios per player for each 3-year period.1 Dependent t tests were performed on both the two- and three-point completion percentages for each 3-year period. A statistically significant difference was obtained for the three-point completion percentages between the first baseline condition (1991–1994) and when the three-point distance was decreased (1994–1997), t(170)  =  6.55, p < .05. The difference between when the three-point distance was decreased and the second baseline condition approached significance, t(170)  =  −1.56, p  =  .061.

Table 1.

Mean Values for Two- and Three-Point Attempts, Completions, Completion Percentages, and Mean Log Response and Reinforcement Ratios per Player for Each 3-Year Period

M	1991–1994	1994–1997	1997–2000
2-point attempted	766.111	610.637	455.023
2-point scored	377.83	302.614	213.041
2-point shooting %	48.8	48.8	45.7*
3-point attempted	115.631	208.760	126.427
3-point scored	40.199	77.456	45.643
3-point shooting %	26.3	32.6*	31
Log response ratio	−1.097	−0.623	−0.76
Log reinforcer ratio	−1.247	−0.797	−0.797

^*p < .05.

For the two-point completion percentages, there was no difference between the first baseline condition and when the three-point distance was decreased, t(170)  =  0.14, p  =  .89. However, there was a statistically significant difference for two-point completion percentage between the second baseline condition compared to when the three-point distance was moved closer, t(170)  =  −7.71, p < .05. Thus, the increase in the relative rate of three-point shots attempted and scored when the three-point line was moved closer could not have been a function of two-point shooting percentages, because there was no change. Also, the decrease in the relative rate of three-point shots attempted when the three-point line was moved back could not be attributed to a decreasing two-point shooting percentage, because this would have made three-point shots appear relatively more reinforcing instead of less.

This study replicates the findings of Vollmer and Bourret (2000) and extends them by demonstrating that changes in the relative rate of reinforcement for three-point shots relative to two-point shots were followed by changes in the relative rate of three-point shots attempted. In this case, the increase in three-point shots made was a function of moving the three-point line closer to the basket. It is unclear why moving the three-point line back did not facilitate a reversal in the relative rate of three-point shots made. Perhaps offensive strategies formulated by coaches when the three-point distance decreased were insensitive to the changing reinforcement contingencies (i.e., rule-governed behavior). Further studies involving naturalistic observations of matching behavior may focus on whether matching is correlated with success in athletics (i.e., do players who come closest to perfect matching score more points on average?). In addition, experimental studies may be conducted using sports video games to test how sensitive athletes and nonathletes are to changing relative reinforcement rates in a more artificial, but better controlled, setting.