Mother–offspring competition promotes colonization success

Abstract

Colonization is the crucial process underlying range expansions, biological invasions, and metapopulation dynamics. Which individuals leave their natal population to colonize empty habitats is a crucial question and is presently unresolved. Dispersal is the first step in colonization. However, not all dispersing individuals are necessarily good colonizers. Indeed, in some species, the phenotype of dispersers differs depending on the selective pressures that induce dispersal. In particular, kin-based interactions, a factor driving social evolution, should induce different social response profiles in nondispersing and dispersing individuals. Kin competition (defined here as between the mother and offspring) has been proven to produce dispersers with a particular phenotype that may enhance their colonizing ability. By using the common lizard (Lacerta vivipara), we conducted a multipopulation experiment to study the effect of kin competition on dispersal and colonization success. We manipulated mother–offspring interactions, which are the most important component of kin competition in the studied species, at the family and population levels and measured the consequences on colonization success. We demonstrate that mother–offspring competition at the population level significantly influences colonization success. Increased competition at the population level enhanced the colonization rate of the largest juveniles as well as the growth and survival of the colonizers. Based on these results, we calculated that kin-induced colonization halves the extinction probability of a newly initiated population. Because interactions between relatives are likely to affect the ability of a species to track habitat modifications, kin-based dispersal should be considered in the study of invasion dynamics and metapopulation functioning.

One of the best examples of successful range expansion has been the human colonization of the Earth. Beginning in Africa, humans subsequently colonized all continents, islands, and habitats (1). Many other species can also expand their geographic range, and many species are able to track habitat change. Rather than through a simple diffusion process, colonization seems to correspond to a necessity, reflecting an active process (1). The rapid recolonization of habitats made available by the retraction of glaciers (2, 3) also shows that many species have the capacity to expand their distribution when environmental conditions offer them the possibility (3). A northern range expansion of a species due to global warming (4) demonstrates the importance of colonizing processes that allow a species to track environmental changes (4, 5). Similarly, biological invasions are an extreme example of range expansion that demonstrates clearly the advantages of colonization (6).

Colonization is the movement from a natal or breeding population followed by settlement in an area where no individuals of the same species are currently present (7). Colonization has been most often viewed as a random process in which some individuals reach a suitable new habitat by chance (8). It recently has been suggested that not all dispersers from a source population display the same colonization success and that successful colonizers might display particular phenotypic profiles (9) that enhance their colonization success (10). For example, in Polynesian island societies, a tradition was to send out young and robust people in the expectation that they would find other islands on which to settle (11, 12).

Under what circumstances or in response to which dispersal inducing factor(s) are such phenotypes produced? Dispersal, as the first step leading to successful colonization, is promoted by many different biotic and abiotic factors (10). Among these factors, kin interactions, a factor driving social evolution (13, 14), are involved in the evolution of dispersal (8, 14–18). Indeed, the evidence for kin-competition-based dispersal is starting to accumulate. Kin-mediated dispersal has been suggested to exist in gray jays (19), mice (20), and red foxes (21) and has been demonstrated in voles (22), insects (23), and lizards (24). Kin-based habitat choice also has been demonstrated in a crow (25) and in a lizard (15). Kin competition not only affects the decision to stay or leave but also promotes the dispersal of morphologically and/or behaviorally different individuals (17, 26, 27). Indeed, the amount of kin competition that a juvenile might face at birth can be assessed during pregnancy by the clutch–sex ratio (among offspring competition, hormone leakage) (28) or by the health of the mother (e.g., stress of the mother) (29). The phenotype of juveniles might therefore be modulated to prepare for kin competition at birth. However, other factors inducing dispersal (e.g., inbreeding or intraspecific competition) are harder to assess during pregnancy because the delay between the prenatal environment and the environment at sexual maturity is important (30). It has been demonstrated that prenatal density does not affect juvenile dispersal (31). Therefore, empirical studies have supported the hypothesis that only kin-based dispersers display a specific phenotype. For example, in red-backed voles (Clethrionomys rufocanus bedfordiae), kin competition among littermates (i.e., stronger sister–sister interactions) has been found to induce the departure of the heaviest females (32). More recently, Moore et al. (27) have shown that male pollinating fig wasps (Platyscapa awekei) disperse to avoid kin competition and that this strategy depended on body size. Consequently, the link between kin-based dispersal and phenotype-dependent dispersal now has been demonstrated in a few species (24, 29).

Specifically, kin competition promotes the departure of individuals with morphological traits of better quality, e.g., superior body condition, larger body size (10, 17, 26, 27, 33, 34). Therefore, individuals dispersing for kin-based reasons might be better prepared to support the costs of dispersal and/or of colonizing empty habitats (35). Moreover, studies in the side-blotched lizard have found that dispersal, social tolerance, and disperser morphology are tightly linked (15, 24, 36). This suggests that kin competition might also promote the departure of juveniles with particular behavioral syndromes. Although not directly related to kin competition, evidence that dispersers have different behavioral syndromes than philopatric individuals is accumulating. For example, in the mole rat, dispersers that are larger also display selfishness (37). In the common lizard, juveniles dispersing when mother–offspring competition is expected to be high (high survival prospect for the mother) are attracted by novelties and repulsed by the odor of their mother (29, 38). From these findings, we predict that individuals dispersing for kin-based reasons may display a specific morphology and a particular behavioral syndrome that might enhance their success in empty habitats. In this study, we experimentally tested whether individuals leaving a population with high levels of kin competition had higher colonization success than individuals from populations with low levels of kin competition.

The common lizard has the key attributes needed to test such a hypothesis. First, the presence, condition, and age of the mother, characteristics that reflect the expected risk of a mother–offspring interaction, are cues used by offspring to initiate dispersal (17, 26, 39). Second, offspring dispersal is strongly shaped by mother–offspring interactions (17, 34) and to a lower extent by other components of kin competition [within offspring competition, within offspring same sex competition, father–offspring competition (17, 40)]. Finally, offspring leaving their natal population in response to the presence of their mother have specific morphological and behavioral profiles (17, 26, 34, 39).

To investigate whether kin-based dispersal enhances colonization success, we performed a replicated experiment by creating eight pairs of connected patches with seminatural substrate (41). A replicate consisted of a lizard population in one patch connected by a 20-m long dispersal corridor to a similar-sized patch containing no lizards. The enclosure dimensions corresponded to the average size of a natural home range (in this nonterritorial species, many individuals share the same home range), and the length of corridors corresponded to the mean dispersal distance observed in natural populations (41). The experiment mimicked a situation in which potential colonizers of a source population first emigrate through unsuitable habitat (the corridor), before encountering a new suitable place to settle. Dispersing individuals were identified by capture in pitfall traps before they entered the new population. To assess survival and growth, individuals were recaptured in all patches (for further details, see Materials and Methods). We manipulated kin competition at two levels: first, at the individual scale by manipulating the presence and absence of the mother of juveniles; and second, at the population scale, by varying the proportion of juveniles being released in the presence or absence of their mother in a population (high population relatedness treatment: 67% of the mothers present; or low population relatedness treatment: 33% of the mothers present). Hereafter, we use the term “kin competition” for the effect of the presence of the mother at the individual scale and the term “population relatedness” for the proportion of juveniles in the presence of their mother within a population. Offspring were released either with their mother or with a surrogate female to keep the age and sex structure constant across treatments and populations.

Results and Discussion

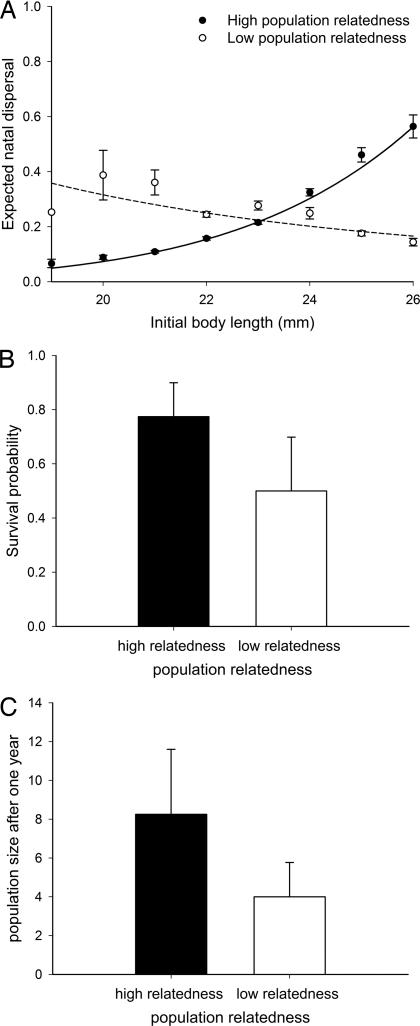
First, we confirmed that kin competition induced the dispersal of individuals with different phenotypes and second, we tested whether these dispersers would show superior colonization abilities. Kin competition at the individual scale had no effect on the dispersal probability, whereas at the population scale, higher population relatedness induced the dispersal of differently sized offspring (Table 1). Offspring dispersing from populations with high population relatedness had significantly bigger body size at birth than nondispersing offspring, and no differences were observed in populations with low population relatedness (Table 1, independent contrasts; high population relatedness: F_1,790 = 9.65, P = 0.0022; low population relatedness: F_1,790 = 0.57, P = 0.4506). This suggests that the strength of the mother–offspring competition was modulated according to the number of offspring experiencing similar conditions in the population, i.e., that mother–offspring competition had a condition-dependent expression. Context-dependent responses to mother–offspring competition have already been found (17, 29), but the previous response was with respect to the female condition not with respect to population characteristics. The difference here is that, in the high-relatedness treatment, mother–offspring competition not only affects juveniles in the presence of their mother but also other juveniles in the same population. Previous studies have shown that the sensitivity of juveniles to the presence of their mother, and therefore the sensitivity to kin competition, is determined prenatally (26, 42). However, our results demonstrate that the reaction to the presence of the mother may also be modulated by the population relatedness and thus postnatally. In our experiment, most mothers were healthy, i.e., high female life expectancy, and thus the sensitivity of the offspring to kin competition should have been enhanced prenatally. Furthermore, because females were randomly assigned to treatments, the sensitivity of the offspring to kin competition was on average similar among all treatment groups. In the high-relatedness treatment, juveniles without mothers, but prenatally sensitized to kin competition, dispersed with a similar likelihood as the juveniles released with their mothers, and thus similar phenotypes dispersed. This indicates that offspring perceived the strength of the kin competition of the juveniles released with their mothers and thus that they relied on these external cues on the population level to decide whether to disperse. There are several possible reasons for this. One possibility is that juveniles in the absence of their mothers used the behavior of other offspring for assessing the likelihood of the future presence of their own mother. Indeed, we know from observations in natural populations that just after laying, some healthy females make large excursions out of their core home range in search of food, i.e., being out of contact with their offspring. The offspring of these females will not be able to assess the presence of the mother to trigger dispersal and might then rely on the number of other offspring being in presence of their mother to estimate the probability that their own mother will still be alive. There are, however, other possible explanations, such as population characteristics (e.g., proportion of senescent females, predation risk) to which juveniles sensitized to dispersal might respond. Previous investigations compared populations in which all offspring were either in the presence or absence of their mother, i.e., with either 100% or 0% of kinship (31). Although that experiment revealed the importance of mother–offspring competition as a factor promoting dispersal in the common lizard, it confounded individual and population level effects and therefore could not fully describe the context in which mother–offspring competition promoted juvenile dispersal. In summary, our results confirm that kin competition promotes the departure of individuals with a specific phenotype, which also has been found in fig-pollinating wasps (27). This result forms the basis for investigating whether the kin-induced phenotype-dependent dispersal induces the departure of individuals with superior colonization abilities. Indeed, offspring dispersing from populations with high relatedness showed significantly bigger body size at dispersal than offspring dispersing from populations with low relatedness [estimate (low relatedness), −3.49 ± 1.29 SE; t test on estimates: value = −2.69, df = 6, P = 0.036; conditional F test: F_1,6 = 7.5, P = 0.03; high population relatedness: 40.69 mm ± 0.75 SE; low population relatedness: 37.43 mm ± 0.85 SE]. Because body size positively predicts competitive ability, reproduction, and survival in the common lizard (43, 44), dispersers from high-relatedness populations should display increased colonization success compared with dispersers from low-relatedness populations (7). Indeed, colonizers (i.e., dispersers settled in an empty patch) from populations with high relatedness survived better [estimate (low relatedness) = −1.59 ± 0.53 SE; t test on estimates: value = −2.99, df = 6, P = 0.0240; conditional F test: F_1,6 = 8.99, P = 0.0240; Fig. 1B] and showed increased body growth rates (the difference between body size at the end of the experiment and the body size at dispersal) in the newly colonized patches than individuals originating from populations with a low level of relatedness [estimate (low relatedness) = −5.62 ± 2.42 SE; t test on estimates: value = −2.32, df = 5, P = 0.027; conditional F test: F_1,5 = 11.36, P = 0.02; high population relatedness: 18.86 mm/yr ± 1.69 SE; low population relatedness: 10.87 mm/yr ± 1.83 SE]. In squamate reptiles, sexual maturity is body-size-dependent (44). Individuals that are bigger at birth or that grow faster should reach sexual maturity sooner. Indeed, our results showed that independent of the treatment, bigger 1-yr old females (body size: F_1,123 = 4335.26, P < 0.0001) and colonizers (F_1,123 = 10.41, P = 0.0016) were more likely to reproduce. However, we did not find any treatment effect (F_1,4 = 0.13, P = 0.7347) on female reproduction, which is not surprising because in this species, females start to reproduce in their second year and only occasionally in their first year (45). However, increased body size should affect reproduction in the subsequent years, because bigger females are sexually mature earlier, have a higher probability of reproduction, and lay bigger clutches (45). Differences in colonization, survival, and growth rates resulted in higher population sizes of the initially empty patches when individuals came from a population with high relatedness compared with populations with low relatedness (logistic regression with Poisson distribution: χ₁ = 6.02, P = 0.014; see Fig. 1C). To measure the impact of the above results on the probability of a successful establishment, we constructed stochastic two-sex models of structured populations in which the means and SEs of the dispersal probability, survival, and fecundity characteristics corresponded to the low and high kin population treatments of this field experiment. (For additional details, see Materials and Methods). The probability of failing to colonize an empty patch for individuals originating from a population with high relatedness was half that of individuals from low-relatedness populations [extinction risk (Pe); high relatedness: Pe = 0.23; low relatedness: Pe = 0.46]. Our results thus provide experimental demonstration that kin competition affects colonization success. We demonstrated that offspring leaving a population because of high overall levels of kin competition were of bigger body size than offspring leaving a population with low levels of kin competition. In the newly colonized habitats, individuals from the high kin-competition populations displayed increased growth rate and survival, and newly founded populations were less likely to go extinct than those founded by individuals from low kin-competition populations. This clearly demonstrates that the colonization ability of an offspring depends on the level of kin competition experienced in its natal population. In an earlier experiment, we found that individuals of bigger body size preferentially colonized empty habitats (46), which shows that the likelihood of colonizing empty habitats might also be increased because in high-relatedness populations, bigger individuals were more likely to disperse. Together, these results suggest that kin competition is a key factor in the colonization processes, at least in the common lizard. Specifically, in situations in which individuals leave their natal populations because they have no other choice than to settle in empty patches (e.g., isolated or introduced populations), those leaving the population for reasons of kin competition will have better colonization success.

Table 1.

Effects of kin competition on natal dispersal probability at the individual and population levels

Factors	Estimates ± SE	t for estimates (P)	F statistics (P)
Intercept	−13.0 ± 3.55	−3.65 (0.0003)	—
Family kin competition (SF)	0.27 ± 0.24	1.14 (0.26)	F1,807 = 1.34 (0.25)
Relatedness (L)	11.99 ± 4.56	2.63 (0.039)	F1,6 = 0.34 (0.57)
Initial body length	0.45 ± 0.15	3.01 (0.003)	F1,807 = 0.78 (0.38)
Sex (M)	0.47 ± 0.25	1.89 (0.06)	F1,807 = 3.19 (0.07)
Initial body length × relatedness (L)	−0.53 ± 0.20	−2.73 (0.0065)	F1,807 = 7.45 (0.0065)

Estimates are given for offspring released with a surrogate female (SF) released in low-relatedness populations (L) and for male (M) offspring. Dispersal probability was modeled with mixed-effect logistic regressions by using the glmmPQL function in R 2.0.1. The initial model included the effects of the experimental treatments (at the individual and population level), sex, body size at birth, and interactions as fixed factors, as well as enclosure nested within the population treatment and family nested within both enclosure and family treatment as a random effect. The final model was obtained by backward elimination, dropping in a stepwise process all of the nonsignificant effects. Statistical tests are t tests for the estimates of the model and conditional F tests for fixed effects.

Fig. 1.

Effect of population relatedness on parameters of colonization success. (A) Offspring-dispersal probability from the source population. Offspring dispersing from populations with high relatedness had significantly bigger body size at birth than nondispersing offspring, and no differences were observed in populations with low relatedness (Table 1; independent contrast high population relatedness: F_1,790 = 9.65, P = 0.0022; low population relatedness: F_1,790 = 0.57, P = 0.4506). The data have been back-transformed from values predicted by the logistic regression; each circle corresponds to a single individual. The fitted curves are represented for high population relatedness (solid line) and for low population relatedness (dashed line). (B) Survival of colonizers in relation to the average relatedness of the source population. Colonizers from populations with high relatedness survived better than individuals originating from populations with low relatedness (F_1,6 = 8.99, P = 0.0240). The values are least-square mean ± SD. (C) Population size in relation to the average relatedness of the source population. The population size of the empty patches was significantly higher when individuals originated from a population with high relatedness compared with low relatedness (logistic regression with Poisson distribution, Proc GENMOD: χ₁ = 6.02, P = 0.014). Values are means ± SE.

Theory suggests that kin-based dispersal is important for most species (47, 48), except for those living in metapopulations with high levels of local extinction and species living in successional habitats. As mentioned above, evidence for the existence of kin-based dispersal or habitat selection is accumulating. This suggests that technical difficulties rather than its rarity may be the reason that the effect of kin competition on dispersal and habitat selection has been overlooked (10). The generality of our findings will also depend on the extent to which kin-based problems promote the departure of individuals with particular morphological or behavioral phenotypes. Although particular morphological, physiological, and/or behavioral phenotypes of dispersers have recurrently been found in many studies [reviewed elsewhere (10, 33, 49)], the link between a given dispersal cause and a given dispersal-dependent phenotype has been assessed in only a few species (32). Work on one insect, one lizard, and one mammal species (24, 27, 32) has showed that different components of kin competition (sister–sister, among offspring, and mother–offspring) lead to different dispersal phenotypes. The breadth of taxonomic examples suggests that the link between kinship and dispersal is not taxonomically constrained. Finally, the extent to which kin-based dispersers of other species will display higher colonizing abilities relative to other types of dispersers remains to be discovered because no other studies have examined this hypothesis.

However, if proved as a general rule, the above results are likely to have important implications for the study of invasions, range expansion, and metapopulation processes in which colonization is a driving force behind population dynamics. Whenever the level of kin interactions within a population increases, the capacity of this population to produce good colonizers should be modified. For example, small, introduced populations, which are likely to rapidly build up high levels of relatedness (50), should export a greater number of good colonizers. The repetition of such situations could potentially lead to an invasion (51). In the same way, range expansions due to global warming could be accelerated or decelerated depending on kin structure along the habitat margins. Because kin interactions are a widespread phenomenon that all species encounter, our findings are likely to be general. Species might, however, vary in the extent to which dispersal evolution has been driven by kin interactions or in the way they can assess population relatedness. Further studies comparing species with different modes of habitat occupation (such as sedentary versus vagrant species) will help assess the generality of our results and our predictions. Evaluating the role of kin interactions in dynamical processes is likely to be an important issue in population dynamics because it is in the evolution of dispersal and sociality. Our results further stress that accounting for kin structure and kin competition in conservation policies and reintroduction programs may have important consequences for the conservation of animal species.

Materials and Methods

Experimental System.

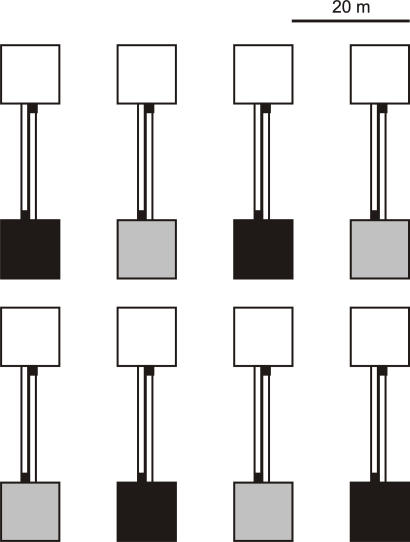
The experiment was conducted in 2003 at the Ecological Research Station of Foljuif (Seine-et-Marne, 48°17′N, 2°41′E). Lizards were maintained in eight enclosed patches (10 × 10 m) containing natural habitat, which offered seminatural conditions. The enclosure size corresponded to core home-range size of the individual under natural conditions (41). However, home ranges overlap in this species, and 30 adults can be found within a similar area size in natural conditions (45, 52). The densities used in this experiment were similar to densities observed in natural populations (41). Pairs of enclosures were connected by two one-way corridors (20 m, Fig. 2). Conditions in the corridor did not allow lizards to settle permanently (almost no direct sun light and poor vegetation, i.e., a hostile habitat for lizards because thermoregulation is impossible), thus excluding the possibility that a lizard is crossing the corridor as part of its everyday movements. A 30-cm deep pitfall trap at the end of each corridor allowed for the daily capture of dispersing lizards. Lizards captured in pitfall traps are referred to as dispersers, whereas lizards that stayed in their populations are referred to as residents (i.e., philopatrics). The length of the dispersal corridors corresponded to the minimal dispersal distance observed in natural populations (41). Indeed, the diameter of the home range of an adults is between 20 and 30 m in natural populations (45). In our experimental system, the distance between the centers (where juveniles were released) of the two connected enclosures was 30 and 25 m between the center of an enclosure and the pitfall trap. In nature, individuals that move 30 m or more from their natal site have been defined as dispersers because these individuals rarely return to their natal site [2% of all individuals (40)]. Rates of secondary movements observed in natural populations are similar to the one observed in our design. Our experimental measure of dispersal directly corresponds to the distance moved by dispersers in nature. Moreover, in our experimental system, the timing of dispersal as well as the dispersal rate are similar to those observed in nature [≈20% (M. Massot and J. Clobert, unpublished data)]. Most of the results found in our experimental systems matched observations from our long-term study or in experiments done by using natural populations [e.g., effect of the presence of the mother (26, 34) and density-dependent dispersal (53, 54)]. Therefore, our experimental system seems to mimic conditions found in natural populations.

Fig. 2.

Experimental design. Gray indicates enclosures in which 67% of the offspring were released with their mother (i.e., populations of high kin competition), whereas black indicates enclosures in which 33% of the offspring were released with their mother (i.e., populations of low kin competition). White indicates enclosures that were initially empty. Pitfall traps at the end of each one-way corridor are represented in black. (Scale bar, 20 m.)

Kin Competition Treatments.

In June 2003, we established lizard populations in eight enclosures (one lizard population per enclosure) (Fig. 2). Each populated enclosure was connected to an empty enclosure by a dispersal corridor. Populations were initiated with 10 adult males, 18 adult females, 12 yearlings (6 males and 6 females), and 103.3 ± 3.08 SE juveniles. These patterns corresponded to the age and sex structure and to the density of natural populations from which the introduced individuals originated (45). All lizards used in this experiment had been housed for at least 1 yr in seminatural populations located at the Ecological Research Station of Foljuif. At the start of the experiment, all lizards were collected over 2 consecutive days. Females were maintained in the laboratory until they gave birth (34), and males were released into the empty populations a few days after capture. Kin competition may occur among parents and offspring, as well as among offspring. In the common lizard, Massot and Clobert (40) did not find evidence for kin competition among offspring in their 18-yr study in natural populations (no correlation between offspring dispersal and clutch size), and they found only weak evidence for same-sex offspring competition [weak correlation between offspring dispersal and clutch sex ratio (35)]. Nothing is known about father–offspring competition, but because females are polyandrous (54) and no parental care exits in this species, this type of kin competition should be less important. However, mother–offspring competition was repeatedly found to be crucial (see Introduction), indicating that it is the major component of kin competition in this species. We therefore modified kin competition by manipulating the presence of the mother. The results obtained in this experiment were consistent with these findings, because mother–offspring competition, but not offspring competition (measured by clutch characteristics) did affect the dispersal probability (clutch size: χ₁ = 1.62, P = 0.20; clutch–sex ratio: χ₁ = 1.08, P = 0.30). Two days after birth, all offspring of a family were released with their mother or with a surrogate female to manipulate kin competition at the individual scale. To manipulate kin competition at the population level, we released in four of the eight populations six families with their mother and 12 with a surrogate female, and in the remaining four populations, we released 12 (67%) families with their mother and six with a surrogate female. These levels of kin structure were selected because they correspond to the upper and lower limits of adult female survival rates observed in our long-term study (42). Families were randomly selected to be released with or without their mothers, and populations were randomly distributed among treatments. Family characteristics (i.e., body length of the female released, number and body length of offspring) were not significantly different between the two kin-competition treatments (individual and population scale), and there were no interactions (P > 0.1). These findings show that the starting conditions were indeed random with respect to the treatments.

Field Monitoring.

Lizards were individually marked by toe clipping, and both snout-vent length and body mass were measured before release. Body condition was defined as body mass relative to snout-vent length, by adding snout-vent length as a covariate in our analyses. Pitfall traps were checked daily to monitor dispersal. Dispersers were identified, measured (snout-vent length and body mass) and thereafter released into the arrival enclosures. Some dispersers attempted a secondary dispersal from the arrival enclosures. These secondary dispersal attempts were not dependent on population relatedness (F_1,6 = 1.47, P = 0.2709), and the secondary dispersers were subsequently released in nonexperimental enclosures. To measure survival probability and growth rate, we recaptured all surviving individuals in May 2004, almost 1 yr after release. To ascertain that no individuals were left in the enclosure, we conducted 10 successive recapture sessions. Immediately after capture, lizards were brought to the laboratory, where they were measured and housed until the end of the tenth capture session. The escape-proof enclosure and the absence of living lizards during the last six recapture sessions allowed us to ascertain that all survivors were recaptured.

Statistics.

Dispersal probability, colonizer survival, and reproduction probability were modeled with mixed effects logistic regressions by using the glmmPQL procedure in R 2.4.0 (55). These mixed-effect logistic regressions fitted the data well, as shown by the Pearson χ² statistics of the initial models. The body size at dispersal and average growth rate of colonizers were modeled by using the lme procedure in R 2.4.0 (55). The normality and homoscedasticity of the residuals of these models were approved in all cases. All initial models included the following factors: experimental treatments (at the individual and population level), sex, body size at birth, and interactions as fixed effects as well as the enclosure nested within the population treatment and family nested within the enclosure factor. For the analyses on the morphology of the colonizer (body size at dispersal, average growth rate, survival), the date of dispersal was added as a covariate to control for individual variation in timing of dispersal and therefore growth. The best model was obtained by backward elimination, i.e., dropping in a stepwise process all nonsignificant effects (P < 0.05). Statistical tests are conditional tests for fixed effects. Conditional tests for the significance of a term in the fixed effects specification are given by the usual F tests based on the usual (REML) conditional estimate of the variance (56). We also provide t tests on the estimates of the model fit by maximum likelihood.

Population Model.

Stochastic two-sex models (57, 58) were used to compare the overall colonization success across treatments. We modeled the population growth rate in the colonized patch during the first year of the colonization process (from establishment of the source population in August year t to the last recapture session in June of year t + 1). The postbreeding census lifecycle graph (58) describes the juvenile class that is the colonizing age class in our experiment. The demographic parameters characterizing the newly founded populations are the means over replicates of survival, fecundity, and immigration rate split by sex and treatments (high versus low relatedness). The model included demographic stochasticity of survival probability with a binomial distribution and of fecundity with a Poisson distribution. Environmental stochasticity was included for survival by using means and standard errors at the replicate level. For each combination of parameters, 100 population trajectories of 1-yr length were drawn by using Monte Carlo simulations. Extinction probabilities were computed as the number of extinct trajectories over the total number of simulated trajectories (59). Simulations were performed with the ULM computer program (60).