Mechanisms for climate-induced mortality of fish populations in whole-lake experiments

Abstract

The effects of climate change on plant and animal populations are widespread and documented for many species in many areas of the world. However, projections of climate impacts will require a better mechanistic understanding of ecological and behavioral responses to climate change and climate variation. For vertebrate animals, there is an absence of whole-system manipulative experiments that express natural variation in predator and prey behaviors. Here we investigate the effect of elevated water temperature on the physiology, behavior, growth, and survival of fish populations in a multiple whole-lake experiment, by using 17 lake-years of data collected over 2 years with differing average temperatures. We found that elevated temperatures in excess of the optimum reduced the scope for growth through reduced maximum consumption and increased metabolism in young rainbow trout, Oncorhynchus mykiss. Increased metabolism at high temperatures resulted in increased feeding activity (consumption) by individuals to compensate and maintain growth rates similar to that observed at cooler (optimum) temperatures. However, greater feeding activity rates resulted in greater vulnerability to predators that reduced survival to only half that of the cooler year. Our work therefore identifies temperature-dependent physiology and compensatory feeding behavior as proximate mechanisms for substantial climate-induced mortality in fish populations at the scale of entire populations and waterbodies.

As our climate continues to warm, there must be corresponding direct effects on animal populations because the two fundamental physiological components of growth, consumption and metabolism, are strongly affected by temperature (1). Populations are often highly adapted to their local climates, and so increases in temperature in excess of their evolved optimum value for growth (2) must reduce maximum consumption rates and increase metabolic rates (1). Resultant decreased growth may lead to negative effects on important ecological processes that depend on body size. For instance, low growth rate and small body size reduce survival of juvenile fish faced with risks of starvation and predation (for review, see ref. 3). On the other hand, compensatory (or catch-up) growth is common in fishes (4), resulting from greater foraging effort to increase food consumption (5, 6). Thus, fish may behaviorally compensate for poor growing conditions caused by climate. However, although greater foraging effort will increase growth, it can also result in greater mortality rates because of greater visibility to, and encounter rates, with predators (7, 8).

Although we now have a broad perspective on the potential impacts of a warming climate on a variety of plant and animal populations, including fish (9, 10), there is an absence of truly large-scale manipulative experiments in vertebrate animal populations. As a result, we have a good understanding of the effects of climate warming on processes that impact individuals, but assessments of the outcome of these processes at the population level remains unclear (9). For instance, we know of no whole-system replicated field experiments directly documenting climate-driven effects on survival and growth in a vertebrate population. Yet, such experiments are critical to our understanding of climate impacts because the common large-scale correlative, and small-scale manipulative experiments, do not possess the realism or experimental control necessary to make convincing links between effects on individuals and populations-level outcomes.

Here, by using entire lakes as replicates, we show that relatively small increases in water temperature can dramatically reduce survival in experimental fish populations, and we identify the temperature-dependent physiological and behavioral mechanisms responsible for it. We exposed closed experimental populations of age-0 rainbow trout (Oncorhynchus mykiss) in a set of small lakes to a consecutive warm and cool year (eight and nine replicate lake populations, respectively), and we provide evidence for a behavioral mechanism that compensates for low growth efficiency in warm years but incurs a high-mortality cost. On the basis of known temperature-dependent consumption and metabolism rates for rainbow trout, we predicted that for a given level of food abundance, trout growth is depressed in warm years compared with years when trout growth is near its optimum temperature (11). An optimum results from the simple fact that maximum consumption follows a dome-shaped function with temperature, whereas metabolism increases exponentially with temperature (1, 12). These facts led us to make two quite different predictions. First, decreased growth efficiency at high temperatures could reduce growth and survival because of an extended period of exposure to size-dependent predation while foraging (3). If so, we should observe that survival depends on realized growth rate and that growth rate declines at high temperatures. Alternatively, decreased growth efficiency at high temperatures could result in compensatory behavior, whereby trout increase foraging activity to maintain growth but, because of greater activity-dependent exposure to predation risk, they experience lower survival. To isolate the effect of climate from other variables known to affect fish survival and growth, we quantified and statistically controlled for variation in food abundance among lakes as well as fish density. Previous studies have shown that adult trout are the only major source of mortality for young trout in these lakes (13, 14), and young trout grow quickly in these productive lakes [i.e., starvation does not occur (15)]. Although variation in the density of adult trout predators varied among lakes, it is the activity-dependent vulnerability of young trout to them that determines mortality and not variation in predator density (7, 8, 15).

Results and Discussion

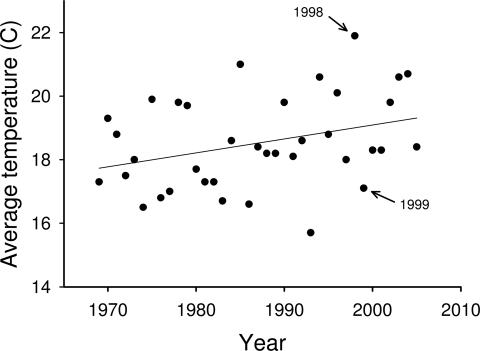
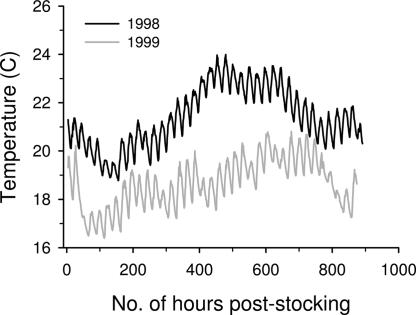
We found that average July air temperatures have increased over time between 1969 and 2005 at Merritt, BC, Canada (F_1,35 = 4.2, P < 0.05; Fig. 1). The average July temperature in 1998 was the highest on record (21.9°C), whereas 1999 was among the lowest (17.1°C; Fig. 1). Not surprisingly, there was a close correspondence between July air temperatures and average water temperatures from early July to mid-August; average littoral water temperatures were 2.7°C warmer in our lakes in 1998 (mean, 21.4; range, 20.5–22.1°C) than in 1999 (mean, 18.7; range, 17.5–19.8°C; F_1,15 = 90.7, P < 0.0001; Fig. 2).

Fig. 1.

Mean July air temperatures from 1969 to 2005. Solid line represents the significant (P < 0.05) linear increase in temperature over time. Labeled are the 2 years for which we present comparative survival, growth, and behavior of young trout in small lakes (1998, n = 8 lakes; 1999, n = 9 lakes).

Fig. 2.

Average (across eight or nine lakes) hourly temperatures in the littoral zone from stocking in early July to mid-August in the experimental lakes in 1998 and 1999. Every 100 h represents just over 4 days for a total of ≈37 days (or 900 h) total duration. Hourly temperatures are shown to illustrate the variation in water temperature over the entire day and to show lack of temperature overlap between years.

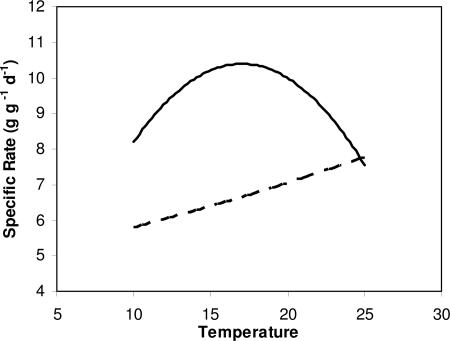
We calculated that trout maximum consumption declines rapidly with temperature in excess of the optimum (≈17.5°C), and metabolism increases exponentially with temperature (Fig. 3). Even though our temperature-dependent rates were calculated from data on trout larger than used in the present experiment (12), the optimum for growth corresponds almost identically to the 18°C optimum determined for age-0 trout (11). Given the patterns of temperature-dependent consumption and metabolism, trout must increase consumption rates to keep growing when temperatures increase (Fig. 3). Water temperatures in 1999 were at or near the optimum for growth for much of the time, whereas in 1998 temperatures were frequently in excess of 20° and even 22°C (i.e., 1–3°C above the optimum range). Therefore, if fish were consuming maximum rations, then growth rates must be lower in 1998 compared with 1999. If, however, prey consumption by fish was submaximal, then fish could either grow more slowly or increase consumption in 1998 to maintain growth rates (Fig. 3).

Fig. 3.

Temperature-dependent rates of metabolism (dashed line) and maximum consumption (solid line) for rainbow trout (see Methods). Note that the maximum growth rate and the scope for growth (difference between maximum consumption and metabolism) decline with increases in temperatures above 17.5°C and become zero at 25°C.

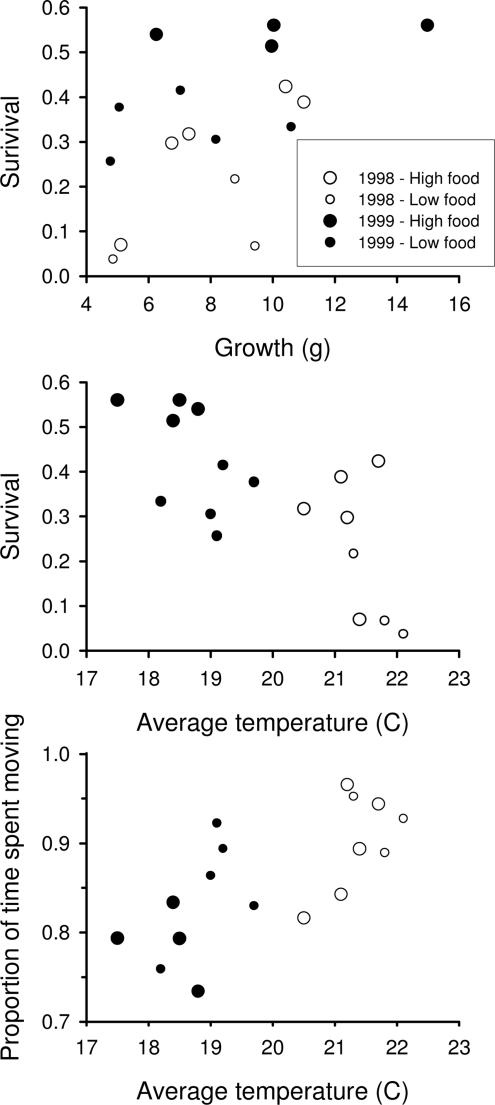
Contrary to our first prediction, we found that survival was not related to growth rate, and growth rate did not vary with temperature. First, survival of age-0 trout was not related to growth rate because it was not more likely than a null model containing only a constant (model 2 vs. 1; Δ_i between these two models, 1.8; Table 1 and Fig. 4 Top). Second, growth of age-0 trout was constant (model 1) and did not vary with temperature, food abundance, or density (Table 1; see also Fig. 4 Top). Including any additional interaction effects did not improve model fits (all Δ_i > 3.0), and they were therefore not included in Table 1. Use of the number of hours above 20, 22, or 24°C in place of average temperature did not improve the fit for models containing temperature (all three Δ_i > 2.0).

Table 1.

Structure and fit statistics for models predicting survival, growth, and activity of age-0 trout populations as a function of growth rate, food abundance, temperature, and trout density

Model	Formula	Survival			Growth			Activity
		R2	AICc	Δi	R2	AICc	Δi	R2	AICc	14.8
1	c	0	−2.4	13.7	0	15	0	0	−23.8	8.4
2	c + growth	24	−4.2	11.9	NA			NA
3	c + food	21	−3.3	12.8	10	16.2	1.2	2	−21.0	11.2
4	c + temperature	52	−11.9	4.2	7	16.8	1.8	45	−30.3	1.9
5	c + density	7	−0.7	15.4	6	17	2.0	1	−20.8	11.4
6	c + growth + temperature	62	−12.5	3.6	NA			NA
7	c + food + temperature	70	−16.1	0	16	18.5	3.5	47	−27.2	5.0
8	c + density + temperature	53	−8.7	7.4	24	16.9	1.9	61	−32.2	0
9	c + food + density	27	−1.3	14.8	16	18.5	3.5	2	−17.4	14.8
10	c + food + density + temperature	70	−12.4	3.7	33	18.8	3.8	62	−28.3	3.9

AICc values (smaller is better), Δ_i values comparing each model with the one with lowest AICc value, and R² values are presented for each. Only models containing the main effects are shown for clarity because all interaction effects did not improve model fit in any instance (see Results). Values in bold indicate the most likely model given the data. NA, not applicable.

Fig. 4.

Survival of age-0 trout. (Top) Survival in relation to growth rate. (Middle) Survival in relation to average water temperature. (Bottom) Proportion of time spent moving by individual age-0 trout in the littoral zone (where most reside) in relation to average water temperature. Each datum represents the estimate obtained for an entire trout population in a given experimental lake; n = 17 lake populations in total.

In support of our second prediction, we observed that trout survival declined predominantly with temperature and that trout activity rates increased with temperature. Trout survival decreased with increases in temperature (Δ_i = 9.5, model 4 vs. 1, R² = 0.52), and survival was most strongly related to a combination of average temperature and food abundance (R² = 0.70; Table 1, model 7; Fig. 4 Middle). As in previous analyses, including interaction effects did not improve the fit of any of the models (all Δ_i > 3.0), and use of alternate measures of temperature did not improve the fit of any models containing temperature (all three Δ_i > 2). Activity (proportion to time spent moving) of individual trout foraging in the littoral zone increased with temperature and their own density (R² = 0.61, best-fit model 8; Fig. 4 Bottom); however, a simpler model with only temperature (R² = 0.45, model 4) was equally likely (Δ_i < 2) and explained most of the variance of the model containing both predictors (Table 1 and Fig. 4 Bottom). As before, interaction terms (all Δ_i > 3.0) and use of alternate temperature measures (all Δ_i > 2) did not improve model fit.

We have shown that relatively small increases in water temperature caused by climate, in excess of the optimum for growth for rainbow trout, substantially reduced survival of trout populations. Fewer than half as many trout survived on average when temperatures were above the optimum rather than near the optimum. Those populations at high temperatures and low food abundance experienced the lowest survival, whereby only a few percent of the original cohort survived their first growing season before winter. After statistically controlling for the effects of food abundance on survival, direct temperature effects accounted for substantial variation in survival, leaving relatively little unexplained variation in the data. Although we had only 2 years of data to assess the temperature effect on survival, significant within-year replication suggests that our results are highly robust. For instance, we had eight and nine whole-system replicates in each year, with each replicate system differing from one another in terms of lake productivity, morphometry, and size. Low residual variance in the data indicates that any remaining factors (other than food abundance and trout density that we statistically controlled for) that might influence behavior, growth, and survival and that were not accounted for by this work, are unlikely to be important (e.g., lake morphology or habitat structure differences).

In addition to demonstrating significant direct survival effects on fish resulting from climatic-driven temperature differences, we also identify physiological and behavioral mechanisms that underlie the patterns of survivorship. Reduced scope for growth at higher temperatures did not reduce growth rates in fish populations, but rather individual fish increased their foraging effort through greater activity levels, leading to greater predation mortality. Elevated activity in trout and other animals is known to increase feeding and growth rates but reduces survivorship because of greater visibility to and encounter rates with predators (7, 8, 16). Thus, we have demonstrated here the magnitude of the population-level consequences of temperature-dependent physiological and behavioral mechanisms operating at the individual level in a variable and changing climate.

Effects of climate change on plants and animals have been broadly documented (10), although few studies exist at large spatial and temporal scales or at whole-population levels. By contrast, this work is a controlled and replicated whole-system (whole-population) evaluation of climate effects on a vertebrate animal population. Our results also have important implications for understanding mechanisms leading to population decline in a warming climate, in particular for fisheries on which we are so dependent. As pointed out by Parmesan (9), projections of climate impacts will require a better mechanistic understanding of ecological and behavioral responses to climate change and climate variation. In particular, our study illustrates well how individuals within populations can compensate behaviorally for poor growing conditions related to elevated metabolism in a warming climate. In fact, it seems as although the fish modify their behavior to achieve a target growth rate (an intrinsic growth rate), or autumn body size, rather than being passively affected by temperature and growing slowly as temperatures rise. It is interesting to point out that observed mortality was related to greater risk taking by young trout attempting to maintain growth rates rather than to predator density. In fact, adding predator density into our statistical models had no effect (data not shown), as we have shown previously (7, 15, 17), suggesting that mortality rates of young trout are determined largely by their behavior. Given the observation of behavioral compensation in this work, predictions about climate effects based solely on an understanding of temperature-dependent animal growth determined in the laboratory can be erroneous. For instance, temperature effects on growth from the laboratory would predict a reduction in growth rate of trout, whereas we observed that growth rate was maintained in warm conditions.

Not surprisingly, we identified significant increases in water temperatures as being related to a trend for increasing summer air temperature in recent decades. Given the wide variation in temperatures about the trend line, warm years that will lead to detrimental effects on fish populations will become more common and more severe. In particular, when average summer temperatures rise to 24°C, trout will not be able to grow at all because there is no scope for growth, and therefore behavioral compensation is not possible. As a consequence, we predict increasing frequency of poor or failed year-classes in the future because, in contrast to marine systems where migration is possible, fish cannot emigrate from lakes. Given current climate-warming scenarios, modest increases in temperature of the magnitude we show here can severely impact the tens of thousands of cool- and cold-water recreational and commercial freshwater fisheries in North America, potentially costing economies tens of millons of dollars in lost revenue.

Methods

Data used in this work came from experiments conducted in 1998 and 1999 (7, 18). Our experiments were performed in a set of nine experimental lakes located within 5 km of one another in southcentral British Columbia (BC), Canada. The lakes are small [<5 hectares (ha)] and contain no natural fish populations. Nonetheless, these lakes possess all of the morphological and limnological features present in much larger lakes, and fish introduced into them display all of the normal predatory and antipredator behaviors observed in larger systems (13, 15). Eggs and sperm were collected from a nearby wild population in Tunkwa Lake, BC, and young were raised at the Fraser Valley Trout Hatchery (Abbotsford, BC). Age-0 trout were stocked on July 10, 1998 at a density of either 1,500 or 15,000 fish per ha within several days of completely absorbing their yolk, at a mean length of 27 mm and mean mass of 0.146 g (n = 200). Stocking in 1999 occurred on July 12 at 15,000 fish per ha (27 mm and 0.152 g, n = 200). Stocking took place about the time young trout normally emerge into lakes in local wild populations. Replicate batch samples of age-0 trout were weighed, and all individuals were counted to obtain a mass density that was used to estimate the number to be stocked. Age-0 trout dispersed around the entire littoral zone of each lake and fed actively within 24 h of stocking. Density of predatory (cannibalistic) age-1 and older trout in the lakes varied between 200 and 400 trout per ha, but we have shown previously that variation in density within these ranges has no effect on young trout survival (7, 13) beyond the effect resulting from their presence (13, 19). Therefore, we do not consider this factor in our analyses. Details about the experimental lakes and specific lakes for each density treatment are found elsewhere (7, 18).

To test for behavioral compensation caused by warm temperatures, we quantified the foraging activity of trout in all lakes and years. Activity of individual age-0 trout was determined by direct observation of individuals residing in the nearshore littoral zone where most young trout reside (7, 18). In 1998, trout were observed July 14–17, July 29–31, and August 8–11. In 1999, they were observed July 16–19, August 1–4, and August 10–13. Observations were made from shore with the aid of polarized glasses. Focal animal observations were made by only two observers in 1999 (P.A.B. and an assistant) and one in 1998 (P.A.B.), between 1000 and 1630 in weather that was consistently bright and calm. Individual fish were selected randomly for observation several minutes after arrival at an observation location. A minimum of 35 (1998) and 75 (1999) individuals were sampled per lake on each date, from 4–10 evenly spaced locations around the lake. All lakes were visited during a 4-day period to minimize the possibility of time or ontogenetic changes in behavior among lakes during a sampling trial. We observed each individual fish for 2.5 min or less for highly active individuals that swam at speeds up to 40 cm/s and could not followed along the shore. The total time spent moving was measured by using a stopwatch until the end of the observation period, where movement was defined as a displacement of >0.5 body length.

We used lethal gillnet sampling during the first 2 weeks of October to estimate fall population size and growth rate. Gillnet densities were standardized among lakes based on lake area and ranged from 400 to 500 m² per ha² per night², following the identical netting effort and protocol used by Post et al. (15) in these same lakes. We set sinking and floating experimental gillnets with graded mesh from 13 to 89 mm (stretched mesh size) for five nights in all habitats. Nets were set during the day and retrieved 24 h later (for additional details about nets and methods, see ref. 20). The summed catch over 5 nights of netting was adjusted to account for the fact that the smallest fish are caught with a lower probability than large fish (see the capture-probability model presented in refs. 7 and 13). We modified their capture-probability model by reanalyzing that same extended data set (years 1993–1999) to account for size bias in the gear for age-0 trout only (omitting older fish). Using the raw binomial data and Proc Genmod (SAS Institute, Cary, NC), we estimated a new mean capture-probability model and found that a model containing fish size and initial density best predicted the proportion of marked fish that were recaptured. Therefore, estimates of survival and growth over the growing season differ slightly from those we presented previously that did not incorporate a density effect (7, 18). We expressed survival as the proportion of stocked fish estimated to have survived and growth rate as the mean autumn mass given identical length and mass at stocking.

Temperature data loggers recorded water temperatures in each lake continuously every hour. To ensure that temperatures were comparable among lakes, we secured data loggers to within 10 cm of the lake substrate, in relatively open habitat, at 0.75-m depth on the west side of each lake. We used average temperature, and the number of hours above 20, 22, and 24°C as four different measures of temperature variation among lakes and years measured over an equal number of days. These values were averaged and summed, respectively, over the period from stocking until mid-August to correspond with our behavioral measures and to correspond with the period over which age-0 trout mortality is highest. For instance, survival of young trout in the presence of larger cannibalistic adult trout increases as a steep nonlinear function of body size in our lakes (21). By late-August, fish have grown sufficiently to have reached the upper asymptotic size-dependent survival (21), and at that time age-0 trout use deep littoral and pelagic habitats that are normally highly risky (7, 13). Survival rates of young trout reach a high asymptote at a length of ≈80 mm (21), which corresponds with observed trout size by late August (7). Average air temperatures over time were obtained from the nearest weather station located at the nearby town of Merritt, BC.

We used empirical data from Myrick and Cech (12) to calculate temperature-dependent consumption and metabolism of trout from a series of experiments conducted with rainbow trout that were fed to satiation twice daily. Although they measured routine oxygen consumption directly, we elected to estimate metabolic rate from the series of experiments in which they directly measured both consumption and growth. We used the principle of mass balance to estimate total metabolic rate by calculating the difference between mass-specific consumption and mass-specific growth across a temperature range of 10–25°C. This results in an estimate of total metabolism in units of mass-specific gram equivalents rather than the estimates of routine metabolism in units of oxygen consumption that Myrick and Cech (12) reported. Note that this estimate of metabolism therefore includes the metabolic costs associated with normal routine swimming in tanks and swimming to capture food pellets. We fitted an exponential function to the metabolic rate data (n = 10, R² = 0.74) and a quadratic function to the consumption rate data (n = 10, R² = 0.81) as functions of temperature. Note that we eliminated two clear outliers from their data, both from trials conducted at 22°C.

To control for variation among lakes in food abundance that can affect fish behavior and growth (7, 15), we categorized lakes as high- and low-food abundance based on estimates of pelagic plankton abundance, a strong correlate of food productivity and abundance. Our rationale was twofold: First, age-0 trout are predominantly planktivores (15, 22); second, plankton abundance is notoriously difficult to estimate because of spatial and temporal dynamic fluctuations. Pelagic plankton abundance did not differ between years in low-food lakes or between years in high-food lakes (1998: high = 2,329 μg/liter, low = 949 μg/liter; 1999: high = 2,763 μg/liter, low = 985 μg/ liter; both P > 0.1). However, plankton abundance differed markedly between low- and high-food lakes within years (both P < 0.0005). Additionally, total phosphorus (a predictor of plankton abundance and productivity) differed substantially between low- and high-food lakes during springtime (high: range, 30–53 μg/liter; low: range, 15–22 μg/liter). Details of plankton sampling methods and enumeration are given by Biro et al. (13, 18).

Age-0 trout survival and the proportion of time spent moving by young trout were analyzed assuming normally distributed errors on arcsine square root-transformed data. Mean autumn mass (growth rate) was log-transformed. We compared various statistical models to explain variation in survival, growth, and activity by using the information theoretic criterion, AICc. We considered two models within 2 AICc units of each other as equally likely [i.e., not different (ref. 23)]. This method allowed us to compare nested and unnested models with one another objectively to determine the most probable model(s) given the data. All graphs are presented using the raw untransformed data.

Abbreviation

ha

hectare.