TABLE 2.

Comparison of analysis methods

Estimation method	U		β
Data-driven estimates of the distribution of fixed mutations
Detected mutationsa (Umin, 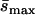)	0.011	0.169	0.076
MLEb (nDEL = 56)	0.028	0.066	0.162
MLEb (nDEL ≤ 56)	0.017	0.109	0.116
Data-driven estimates of the distribution of new mutationsc
MLE (nDEL = 56)	0.030	0.093	0.204
MLE (nDEL ≤ 56)	0.021	0.142	0.141
Model-based estimates of the distribution of fixed mutations
Bateman–Mukai	0.035	0.0269	0d
Maximum likelihoode	0.045	0.0207	0

^aMutations whose fitness effects were detected by the stepwise regression analysis.

^bEstimated using the method of Otto and Jones (2000) by specifying that all of the accumulated mutations were deleterious (n_DEL = 56) or allowing a fraction of the accumulated mutations to be neutral (n_DEL ≤ 56).

^cEstimated by correcting the estimated fixed mutation distributions for the probability that mutations of various effect sizes were lost due to selection during plaque growth.

^dThe Bateman–Mukai analysis method does not estimate Var(s). Rather, it assumes Var(s) = 0.

^eEstimated using the method of Keightley (1994).