The mechanism of addition of pyridoxal 5′-phosphate to Escherichia coli apo-serine hydroxymethyltransferase

Abstract

Previous studies suggest that the addition of pyridoxal 5′-phosphate to apo-serine hydroxymethyltransferase from Escherichia coli is the last event in the enzyme's folding process. We propose a mechanism for this reaction based on quenched-flow, stopped-flow and rapid-scanning stopped-flow experiments. All experiments were performed with an excess of apo-enzyme over cofactor, since excess pyridoxal 5′-phosphate results in a second molecule of cofactor binding to Lys³⁴⁶, which is part of the tetrahydropteroylglutamate-binding site. The equilibrium between the aldehyde and hydrate forms of the cofactor affects the kinetics of addition to the active site. Direct evidence of the formation of an intermediate aldimine between the cofactor and the active-site lysine was obtained. The results have been interpreted according to a three-step mechanism in which: (i) both aldehyde and hydrate forms of the cofactor bind rapidly and non-covalently to the apo-enzyme; (ii) only the aldehyde form reacts with the active-site lysine to give an intermediate internal aldimine with unusual spectral properties; and (iii) a final conformational change gives the native holo-enzyme.

INTRODUCTION

The encounter between cofactors and apo-proteins in the cell is a crucial event that can occur at different stages of polypeptide folding and affect it to a variable extent [1,2]. The form in which the cofactor is available in the intracellular medium may also differ according to its reactivity or toxicity [3]. The role of PLP (pyridoxal 5′-phosphate) in folding and structural stabilization apparently varies among the enzymes which use it as cofactor [4–8]. This is not surprising, considering that there are at least five evolutionary unrelated families of such enzymes, corresponding to completely different protein folds (fold-types I–V) [9].

The mechanism of PLP homoeostasis and targeting to the newly synthesized apoEs (apo-enzymes) is largely unknown. A first step in elucidating this process is to understand how PLP reacts in vitro with a purified PLP-dependent apoE, to form the active holoE (holo-enzyme). We have chosen Escherichia coli and its serine hydroxymethyltransferase (eSHMT) (fold-type I) as our model system because of: (i) the known intracellular distribution and concentration of the B₆ vitamers in E. coli [10]; (ii) the knowledge of the folding mechanism of eSHMT and its relationship to the addition of PLP [8,11–13]; (iii) the availability of a number of important site-specific mutants of eSHMT; and (iv) the published high-resolution structure of the holoE [14].

The mechanism of addition of PLP to several different fold-type I apoEs has been investigated previously for aspartate aminotransferase, glutamate decarboxylase and tryptophanase [15–19]. These studies suggested a three-step mechanism, but were unable to identify unambiguously the structure of the intermediates. Since these studies were performed, advances in rapid-scanning spectrophotometry and in the knowledge of folding mechanisms have provided a new impetus to further research efforts.

The folding mechanism of eSHMT has been investigated in detail and is understood better than that of any other fold-type I PLP-dependent enzyme. It may be divided into two phases. In the first, relatively rapid, phase, two domains fold into their native state, forming an intermediate that has virtually all of the native secondary structure, exhibits most of the native tertiary structure and is a dimer, but is not able to bind PLP. In this intermediate, the N-terminus and an interdomain segment remain exposed to solvent. In the slow (second) phase, the intermediate is converted into the apoE, which is able to bind PLP. Inspection of the crystal structure of the holoE shows that PLP is buried in a deep cavity with no obvious route of entrance or escape to the solvent [14]. Thus, in the apoE, the active-site entrance must be more accessible than in the holoE.

The present study determines the mechanism of addition of PLP to apo-eSHMT and the absorption spectra of all kinetic species involved. The effect of the equilibrium between hydrate and aldehyde cofactor on the kinetics of holoE formation is also determined. Future studies will focus on cofactor specificity and the structure of the protein in all steps of the proposed mechanism. These will use eSHMT site-specific mutants and aldimine complexes of PLP with substrate and non-substrate amino acids.

EXPERIMENTAL

Materials

Ingredients for bacterial growth were from Sigma–Aldrich. Chemicals for the purification of the enzymes were from BDH; DEAE-Sepharose and phenyl-Sepharose were from GE Healthcare. Alcohol dehydrogenase was from Sigma–Aldrich. eSHMT and methylenetetrahydrofolate dehydrogenase were purified as described previously [20,21]. (6S)H₄PteGlu (tetrahydropteroylglutamate) was a gift from Eprova AG. PLP was from Sigma–Aldrich (98% pure). All other reagents were from Sigma–Aldrich. Apo-eSHMT was prepared using L-cysteine as described previously [8]. The apoE was stored in 10% glycerol at −20°C for no more than 3 days before use. The concentration of the apo-eSHMT is calculated from a molar absorption coefficient at 278 nm of 42790 cm⁻¹·M⁻¹. A small residual fraction (approx. 5%) of holoE was always present, as judged by activity assays.

Measurement of PLP molecules bound per monomer of enzyme

Apo-eSHMT samples (10 μM in 1 ml) containing PLP at various concentrations (including control samples from which PLP was absent) were prepared in 50 mM Hepes/NaOH buffer at pH 7.2, equilibrated at 30°C for 30 min and then reduced with NaBH₄ (0.2 M). Reduction of PLP–enzyme Schiff base irreversibly links the cofactor to the protein [22]. NaBH₄ was prepared as a concentrated solution (2 M) in 50 mM NaOH. After 30 min from NaBH₄ addition, samples were concentrated in Amicon Ultra centrifuge filters (30 kDa cut-off) (Millipore) and diluted with Hepes buffer repeatedly, so as to eliminate low-molecular-mass molecules, including reduced free cofactor. The final samples were diluted to 1 ml and an absorption spectrum was recorded. The A₃₃₅/A₂₈₀ ratio was calculated in order to normalize the absorbance of the reduced internal aldimine on the basis of protein concentration, and then divided by the ratio found for a holoE sample. The result gives the fraction of PLP molecules bound per monomer of enzyme.

MS analysis

Two apoE samples (10 μM in 1 ml) were incubated with either 40 μM or 600 μM PLP. A third similar control sample did not contain PLP. After 30 min, 0.2 M NaBH₄ was added to the samples. Low-molecular-mass molecules were removed using centrifuge filters as described above. Proteolytic digestion of each sample (1.5 μg) was performed adding approx. 0.1 μg of modified porcine trypsin (Millipore) in a solution of 25 mM ammonium bicarbonate and incubated at 37°C overnight. MALDI–TOF (matrix-assisted laser-desorption ionization–time-of-flight) analyses of each tryptic peptide mixture were performed in a Voyager-DETM STR instrument (Applied Biosystems).

Activity assays, spectral and stopped-flow studies

The hydroxymethyltransferase activity was measured with L-serine and H₄PteGlu as substrates as described previously [23]. The rate of L-allo-threonine cleavage was measured by coupling the reaction with the reduction of the product acetaldehyde by NADH and alcohol dehydrogenase [24].

Absorbance spectra and steady-state kinetic studies were performed on a Hewlett-Packard 8453 diode array spectrophotometer. Fluorescence emission measurements at equilibrium were carried out at 20°C with a Fluoromax-3 spectrofluorimeter (HORIBA Jobin-Yvon), using a 1-cm-pathlength quartz cuvette. PNP (pyridoxine 5′-phosphate) fluorescence emission spectra were recorded from 350 to 500 nm (1 nm sampling interval; 5 nm emission slit) with the excitation wavelength set at 325 nm (1 nm excitation slit); PNP in the cuvette was 2 μM, while apoeSHMT varied between 0.085 and 6 μM. The dissociation constant for the binding equilibrium was calculated from a Scatchard plot [25]. Curve-fitting procedures and statistical analysis were carried out using Prism (GraphPad Software).

Stopped-flow (absorbance and fluorescence) experiments were performed with an Applied Photophysics SX18 apparatus equipped with a 1 cm optical path observation chamber. A 360 nm filter was applied when measuring fluorescence emission obtained when exciting PNP at 325 nm. Transient spectroscopy experiments were performed with the same apparatus reconfigured with the photodiode array accessory. All experiments were carried out in Hepes/NaOH buffer, pH 7.2, at 30°C.

Chemical quenched-flow experiments

The rapid kinetics of internal aldimine formation were analysed by means of quenched-flow experiments carried out on a BioLogic QFM-400 apparatus, using NaBH₄ as quencher. Borohydride is known to reduce imines and aldehydes rapidly and efficiently [26]. When the internal aldimine of PLP-dependent enzymes is reduced, the cofactor is irreversibly attached to the protein, giving an absorption spectrum with a band at around 330 nm [27].

The four syringes of the quenched-flow apparatus at 30°C contained, respectively, apo-eSHMT (120 μM) in 50 mM Hepes/NaOH buffer at pH 7.2, PLP (20 μM) in the same buffer, water, and NaBH₄ (2 M) in 50 mM NaOH. In each experiment, equal volumes of apoE and PLP (100 μl) were mixed, filling a 200 μl ‘delay line’. Then, water pushed 180 μl of the reaction mixture from the first mixer into the second mixer where it encountered 20 μl of the borohydride solution. The quenched reaction (200 μl) was collected in a vial. The aging time of reactions was determined by the flow speed through the delay line. Five reactions were carried out for each single aging time. In the experiments with aging times longer than 1 s, the flow was interrupted for the desired time interval once the reaction mixture filled the delay line, and then started again in order to quench the reaction. After being quenched, reaction mixtures were left in the vials for 30 min, in order to dissolve the gas bubbles formed from reaction of borohydride with water. Subsequently, the five samples relative to each aging time were pooled (1 ml final volume), concentrated in a centrifuge filter and diluted with 50 mM Hepes/NaOH buffer (pH 7.2) repeatedly, so as to eliminate the low-molecular-mass molecules, including the reduced free cofactor. In the last dilution step, buffer was added to obtain a final volume of 1 ml, and absorption spectra were recorded. The concentration of the reduced internal aldimine was calculated as described above.

Control stopped-flow experiments were carried out in order to compare the rate of NaBH₄ reduction of holo-eSHMT and free PLP in the aldehyde form. The extrapolated half times of the reactions at 0.2 M NaBH₄ (which was the concentration used in the quenched-flow experiments) were calculated to be 0.1 and 3.4 ms for holo-eSHMT and aldehyde PLP respectively.

Data analysis

Binding of PLP to the second site was analysed according to eqn (1), in which N and K_d stand, respectively, for the number of PLP molecules bound per monomer of enzyme and the apparent dissociation constant of the equilibrium.

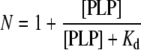(1)

Fitting to eqn (2) returned an initial velocity (v_i) of the reaction in the absence of exogenous PLP (v₀) of 90±3 μM·min⁻¹, while the velocity at infinite PLP concentration (v_inf) was 31±5 μM·min⁻¹ (at pH 7.2 and 30°C; holoE concentration was 0.1 μM).

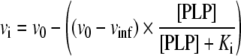(2)

Fitting to eqn (3) gave an v₀ of 45±5 μM·min⁻¹ and a v_inf of 72±6 μM·min⁻¹ (at pH 7.2 and 30°C; holoE concentration was 1.25 μM).

(3)

Eqns (1), (2) and (3) are intuitively derived from the following relationship, that may be generally applied to binding equilibria in which the ligand (in our case PLP) is in large excess with respect to the protein [25]:

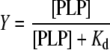(4)

Y is the fraction of enzyme monomers that bind the cofactor at the second binding site, [PLP] is the concentration of free cofactor and K_d is the dissociation constant of the related equilibrium.

Eqn (5) is the sum of three exponential processes [25].

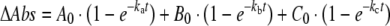(5)

In order to evaluate the accuracy of the fit to the sum of either three or two exponential processes, we performed the F test and the analysis of the explained variance [28]. A comparison of the fits obtained with either two or three exponentials gave an F value of 2.2, which corresponds to a probability of approx. 5% (one-tail; 19 and 14 degrees of freedom for three and two exponentials respectively; analysis carried out on time courses obtained at the four highest apoE concentrations). Fits of the same set of data to either one, two or three exponentials gave variances of 3.93×10⁻⁵, 3.90×10⁻⁵ and 1.77×10⁻⁵ respectively, demonstrating a clear-cut decrease of the explained variance with three exponentials. Finally, the distribution of the fit residuals when fewer than three exponentials were used to fit the data was non-random. These results clearly indicate that data fitted better to the sum of three exponentials.

On and off rate constants (k_on and k_off) for PNP binding kinetics were derived according to Cornish-Bowden [25].

The differential spectra obtained from the rapid scanning experiments were analysed using SVD (singular value decomposition) [29] with the software MATLAB (MathWorks). The analysis was aimed at determining the number of independent spectral components involved in the reaction. Absorption spectra were placed in a rectangular (m×n) matrix A, each column being a spectrum and each row a time course of absorbance at a single wavelength. Matrix A was decomposed using the SVD into the product of three matrices: A=U×S×V^T, where U and V are orthogonal matrices, and S is a diagonal matrix, with its non-zero elements arranged in decreasing order. The columns of matrix U contain the ‘basis spectra’, and those of the V matrix contain the time-dependence of each ‘basis spectrum’. The diagonal S matrix contains the singular values that quantify the relative importance of each corresponding vector in U. Each column of matrix U×S represents a pseudospectrum, i.e. the absorption of one of the spectroscopic components required to approximate the original data and only the first few columns are significant, the last ones having negligibly small values. The signal/noise ratio is indeed very high in the earliest columns of U and V, while the random noise is mainly accumulated in the latest columns.

The global analysis of rapid-scanning stopped-flow data and the band-shape analysis of absorption spectra were carried out using the software Scientist (Micromath). Time traces extracted from the hybrid stopped-flow diode array set of data and the kinetics of formation of the internal aldimine were globally fitted by numerical integration to systems of differential equations describing all possible models (made by reversible monomolecular steps) that would give four independent spectral components when analysed using the SVD. Models were made by: (i) three consecutive reactions; (ii) three parallel reactions; (iii) three reactions branching from a single species; and (iv) two consecutive reactions paralleled by a single reaction. All reasonable combinations of the initial concentrations of components (as well as combinations of components that corresponded to the internal aldimine) were tested. In total, 19 different versions of the four models were tested. Because of the limited capability of the software employed, only nine different time traces (corresponding to the most representative wavelengths) were fitted at once. The capability of the models to fit the data was evaluated on the basis of the distribution of fit residuals. All models except the one made by three consecutive reactions gave clearly non-random residuals. Several different fitting sessions were then carried out according to Scheme 1, so as to cover the entire range of wavelengths acquired (95 different wavelengths).We noticed that the parameters produced by the least-squares minimization routine were somewhat dependent on the initial estimates. To overcome this problem, the set of time courses was simulated over a wide range of the variable parameters in order to map the variance s² in the parameter hyperspace (as suggested by Bevington [30]). The best parameter sets obtained by this procedure were used as the initial estimates in the minimization routines. Often, but not always, different initial estimates converged to the same minimum. In the end, at least two clearly different minima were obtained, and the lower one was chosen as our best description of the experimental data.

Scheme 1.

RESULTS

Evidence of a second PLP-binding site

PLP is a very reactive aldehyde. Before we could analyse the mechanism of PLP addition to eSHMT, we had to make sure that we were observing PLP binding only at the active site. The absorption spectrum of PLP changes radically as its aldehyde group forms an aldimine with the ϵ-amino group of the active-site lysine residue (Lys²²⁹ in eSHMT), yielding the internal aldimine. A comparison between the spectra of free cofactor and holo-eSHMT shows a shift of λ_max from 388 nm to 422 nm, with the maximum absorbance change taking place at 435 nm (results not shown). Following the change in absorbance at 435 nm with a stopped-flow spectrophotometer at different apoE/PLP ratios resulted in complex kinetics (results not shown). Importantly, the shape and amplitude of the absorbance change with a large excess of apoE (100 μM) over PLP (10 μM) were profoundly different from those obtained with a reversed stoichiometric ratio. In particular, with excess PLP, there was a significant increase of the amplitude, suggesting that PLP was adding to at least one additional site.

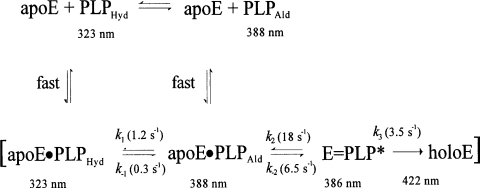
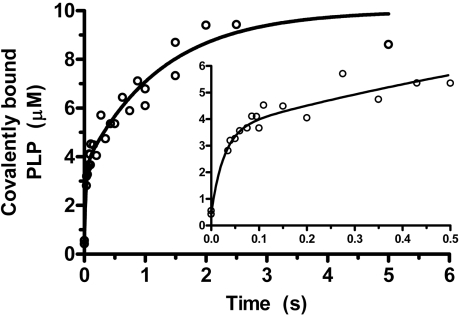
As a test of this hypothesis, at increasing concentrations of PLP the binding was stoichiometric, until a first site was saturated (Figure 1, inset). At higher concentrations, a second molecule of PLP bound, although with a much lower affinity (Figure 1). The best fit of data relative to the holoE to eqn (1), which assumes that one molecule of PLP per enzyme monomer is already bound, yielded a K_d of 230±60 μM for the binding equilibrium of the second molecule of cofactor at pH 7.2 and 30°C.

Figure 1. Equilibrium binding of PLP to eSHMT.

The number of PLP molecules bound per monomer of enzyme (10 μM) was measured as a function of cofactor concentration in 50 mM Hepes/NaOH buffer, pH 7.2, at 30°C. The continuous line through the experimental points (○, apoE; ●, holoE) is derived from the best fit of data to eqn (1). The inset shows the different behaviour of apoE and holoE at low PLP concentration.

Binding of PLP at the second site had an inhibitory effect on the hydroxymethyltransferase activity (results not shown), with an inhibition constant (K_i), calculated by best-fitting the data to eqn (2), of 250±100 μM. On the other hand, binding of the second PLP resulted in an increase of the H₄PteGlu-independent L-allo-threonine cleavage activity (results not shown). Fitting data to eqn (3) returned an activation constant (K_a) of 230±40 μM.

The enzyme residue involved in the covalent binding of PLP to the second site was identified by MS analysis of samples of apoE (10 μM) incubated with either 40 μM or 600 μM PLP. The compared analysis of tryptic peptides showed that the cofactor was bound to Lys²²⁹ in the sample with 40 μM PLP and to both Lys²²⁹ and Lys³⁴⁶ in the sample with 600 μM PLP.

Single-wavelength analysis of holo-eSHMT formation

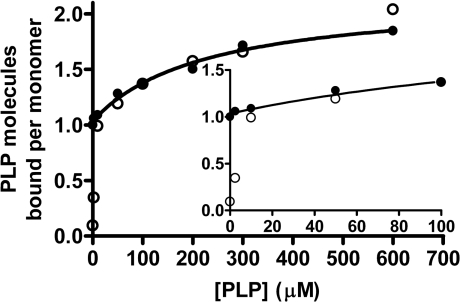
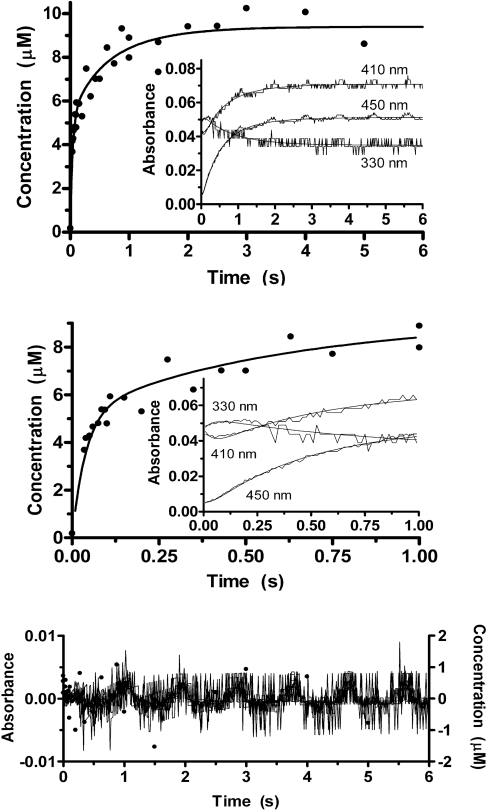
The finding of a second PLP-binding site requires that the studies on the mechanism of addition of PLP be carried out with an excess of apoE over cofactor, to minimize complications in determining a kinetic pathway and to maintain pseudo-first-order kinetics. A stopped-flow investigation was carried out, mixing equal volumes of 20 μM PLP with apoE at several different subunit concentrations (584, 350, 210, 126, 76, 44 and 27.2 μM) and recording absorbance changes at 435 nm (Figure 2). Kinetic traces resulting from the four higher apoE concentrations were virtually superimposable and are well described by the sum of three exponential processes (eqn 5). The sum of two exponential processes did not adequately fit the data, as indicated by the F test and the analysis of variance.

Figure 2. Absorbance changes at 435 nm observed upon stopped-flow mixing apoE and PLP.

Absorbance changes at 435 nm upon stopped-flow mixing equal volumes of 584 (——), 350 (——), 210 (——), 126 (——), 76 (—–), 44 (·······) and 27.2 (-·-·-·-) μM apoE and 20 μM PLP. Conditions were as in Figure 1. The inset shows the lag phase.

Global fitting of the four kinetic traces to eqn (5) indicated that the faster exponential process corresponded to a lag phase with a rate constant k_a=23.8±0.9 s⁻¹ and an amplitude A₀=−0.0074±0.0001 AU (arbitrary units) (Figure 2, inset). This was followed by two exponential increases in absorbance at 435 nm, whose rate constants and amplitudes were k_b=3.44±0.03 s⁻¹, B₀=0.0605±0.0001 AU, k_c=0.53±0.02 s⁻¹ and C₀=0.0110±0.0002 AU. At apoE concentrations lower than 126 μM (before mixing), absorbance changes were systematically slower. The observation that k_a does not change above 126 μM subunit concentration rules out that the lag corresponds to the bimolecular binding step. It rather suggests that a rapid equilibrium, corresponding to the binding of PLP to the enzyme, was established in the dead-time of the stopped-flow instrument. Therefore the lag phase indicates that a reaction intermediate precedes the formation of the 422 nm absorbing internal aldimine.

Rapid-scanning analysis of holo-eSHMT formation

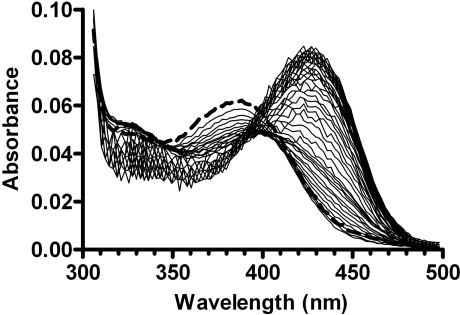
The course of the reaction of PLP with apo-eSHMT was followed by acquiring spectra with the stopped-flow spectrophotometer in the rapid-scanning configuration. Spectra (800) were acquired at 10 ms intervals over a period of 8 s after a 9 ms delay from stop of flow. A control experiment was performed using the same conditions, but with the instrument set up to measure absorbance at a single wavelength (435 nm). Comparison of absorbance changes at 435 nm recorded in the rapid-scanning and single-wavelength configurations revealed that, when spectra are acquired in the scanning configuration, the absorbance change is smaller and takes place with a different kinetic pattern (results not shown). Traces by the two methods are superimposable up to 1 s, but diverge thereafter. A difference in the single-wavelength and rapid-scanning methods is the much higher light intensity used in the latter. A repeat of the rapid-scanning experiment at a lower light intensity showed that photobleaching was occurring after 1 s of reaction (400 spectra were acquired at 16 ms intervals over a period of 6.4 s, after a 14 ms delay from stop of flow). However, the low intensity of light in this experiment yielded increased noise in the data. In order to overcome this problem, a hybrid dataset was created, gathering the first 25 spectra acquired with intense light (at 10 ms intervals, from 9 ms to 0.26 s after stop of flow) and 385 spectra acquired using low-intensity light (at 16 ms intervals, from 0.27 s to 6.4 s after stop of flow) (Figure 3).

Figure 3. Spectral changes observed upon stopped-flow mixing of 120 μM apoE and 20 μM PLP.

Only spectra taken at 20 ms intervals (after 9 ms from stop of flow) with intense light and at 64 ms intervals with low-intensity light are shown for clarity. The sum of the spectra of PLP and apoE obtained after mixing with buffer is shown as a thick broken line. Conditions were as in Figure 1.

Differential spectra of the hybrid dataset (with respect to the last spectrum acquired) were analysed using SVD [29]. The result of the analysis suggested that three independent spectral components were required to describe the experimental data (the S values for the first seven components were 1.36, 0.79, 0.26, 0.18, 0.16, 0.15 and 0.14). Considering that a fourth spectral component has to be added because the analysis was carried out on differential spectra, this interpretation agrees with the single-wavelength studies at 435 nm, described by the sum of three exponential processes.

Two additional experiments, which used intense light, were carried out in which either apoE (120 μM) or PLP (20 μM) were mixed with equal volumes of buffer. No spectral changes were observed in either experiment over a 6 s time period. These experiments gave the spectra of PLP and apoE after mixing (broken line in Figure 3).

PLP in solution is an equilibrium of several different ionic and tautomeric structures with unique absorption properties. At pH 7.2, PLP is mainly present with its ring in the neutral form (approx. 5% of the cofactor is in the anionic form). Both dipolar ionic (where N₁ is protonated and O₃′ is negative) and uncharged tautomers of the neutral ring exist, and each as both aldehyde and hydrate, although the uncharged hydrate is present as a negligible fraction [31]. The spectrum of PLP did not change significantly in the 9 ms after mixing with apoE (Figure 3). We conclude that the rapid-binding equilibrium established in the dead-time of the stopped-flow instrument does not alter the distribution of PLP ionic and tautomeric forms. Spectral resolution with log-normal curves permits a quantitative description of equilibria for hydration and tautomerization [32,33]. The control spectrum of the cofactor after mixing with buffer (which corresponds to the spectrum of PLP at zero time of reaction) was analysed by fitting the experimental data points to the sum of the expected component bands, using Metzler's equation [33]. The parameters returned by the fitting were within ±5% of the values found in the literature. Using the molar absorption coefficients found in the literature, the analysis showed that the uncharged aldehyde (λ_max corresponding to 350 nm) was present as a 28% fraction, while the dipolar ionic aldehyde (388 nm) and the hydrate (323 nm) were present as 52% and 16% fractions respectively. These values are in agreement with literature values for neutral PLP. A fourth band with an absorbance maximum at around 302 nm had to be included in the calculations in order to obtain a satisfactory fit and may account for the remaining 4% of the cofactor. This component may be attributed to impurities and, to a minor part, to the cofactor being in the anionic form, which absorbs at this position. We do not know the exact nature of such impurities; however, the low absorbance maximum may indicate that the carbonyl group is either absent or saturated (and therefore not reactive).

The spectrum of the reaction acquired after 20 ms from stop of flow was also deconvoluted assuming that the absorption bands given by the hydrate form (323 nm) and the material absorbing at 302 nm were unchanged (all related parameters were therefore fixed in the fitting). Only the amplitudes of the bands corresponding to the aldehyde form of the cofactor (350 and 388 nm) were left free to vary during the fitting, while the other parameters were fixed to the values found in the previous deconvolution. A fifth absorption band with a maximum at 335 nm had to be included in order to obtain a good fit. This corresponds to a reaction intermediate generated in the very early phase of the reaction. The amplitudes of both bands relative to the aldehyde form of PLP (350 and 388 nm) decreased. This analysis suggested that only the aldehyde form of PLP reacts in the first few milliseconds of the reaction, giving the intermediate that absorbs at 335 nm.

Quenched-flow analysis

The formation of the internal aldimine between the PLP aldehyde group and the Lys²²⁹ ϵ-amino group was monitored by chemical quenched-flow experiments in which equal volumes of apoE (120 μM) and cofactor (20 μM) were mixed rapidly, and the reaction was quenched at different time intervals with concentrated NaBH₄ (0.2 M). This experiment correctly reports the formation of the internal aldimine only if the aldehyde PLP and the internal aldimine are reduced by NaBH₄ much more rapidly than formation of the internal aldimine. This point was checked by stopped-flow control experiments, which used either holo-eSHMT or free PLP.

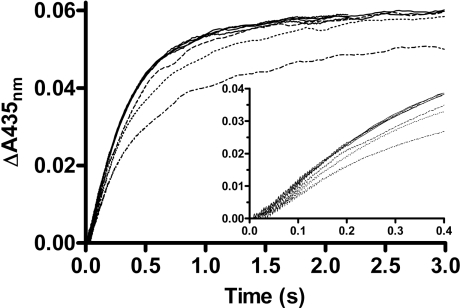
The kinetics obtained fitted well to the sum of two exponential processes with rate constants of 38±16 s⁻¹ and 0.79±0.15 s⁻¹ and amplitudes of 3.1±0.5 μM and 6.4±0.4 μM respectively (Figure 4). A constant 0.5 μM internal aldimine had to be added to account for a small amount of holoE present as a contaminant in the apoE samples. Taking into account the large S.D. of the two rate constants, their values roughly correspond to k_a (23.8±0.9 s⁻¹) and k_c (0.53±0.02 s⁻¹) of absorbance changes measured at 435 nm in the stopped-flow experiments.

Figure 4. Kinetics of Schiff base formation between 10 μM PLP and 60 μM apoE, using chemical quenched-flow.

The experimental points represent covalently bound PLP, and the theoretical line is from fitting to the sum of two exponential processes. Conditions were as in Figure 1. The inset shows the burst in the early phase of the reaction.

Global analysis

Any kinetic scheme describing the reaction between apoE and PLP should be consistent with the results of the SVD analysis of the rapid-scanning data, which indicated the presence of four independent spectral components. To begin with, we tested all kinetic models, made by reversible monomolecular steps, that satisfy this requirement, regardless of their consistency with the chemistry of the system under study. Single-wavelength traces from the hybrid diode array data and the kinetics of internal aldimine formation were globally fitted to all models. Because of the limitations of the software, no more than nine time traces (chosen among the most representative ones) could be fitted at once. Only the model corresponding to three consecutive reactions fitted the data.

A three-step model that is consistent with both our data and the expected mechanism of the reaction is represented by Scheme 1, in which PLP_Ald and PLP_Hyd are the cofactor in the aldehyde and hydrate forms respectively; and apoE•PLP_Ald and apoE•PLP_Hyd are the respective related non-covalent complexes with the apoE; E=PLP* is an intermediate internal aldimine. Fitting data to Scheme 1 (several fitting sessions were carried out so as to cover the entire range of wavelengths acquired), we assumed that, when the stopped-flow registration of the reaction begins, only the species in square brackets are observable and the concentrations of the non-covalent complexes (apoE•PLP_Hyd and apoE•PLP_Hyd) correspond to those of their related free PLP forms. This assumption is justified by the saturation behaviour observed in the single-wavelength experiments (Figure 2) and the results of band-shape analyses. Concentrations of apoE•PLP_Hyd and apoE•PLP_Ald at zero time were, respectively, 1.6 and 8 μM, while those of E=PLP* and holoE were 0. In the global fittings, the concentration of internal aldimine was made equal to the sum of E=PLP* and holoE. The absorbance at any wavelength corresponded to the sum of the concentrations of each of the four kinetic species multiplied by their micromolar absorption coefficient at that wavelength, plus a constant absorbance contributed by the apoE and the band at 302 nm (found in the band-shape analyses and assumed to be mostly inert material; the analysis would have detected any incongruence with this assumption in terms of a poor fit at wavelengths around 302 nm). In the fitting, the molar absorption coefficients of apoE•PLP_Hyd and apoE•PLP_Ald were fixed at the values calculated in the band-shape analysis of the free cofactor, while those of E=PLP* and holoE were free to vary between 0 and infinity. Under the experimental conditions used, either the second or the third reaction (or both) of Scheme 1 must be virtually irreversible. This hypothesis is confirmed by the observation that all cofactor binds covalently to the apoE (Figure 4). The global fit was therefore carried out with three different versions of Scheme 1. Only the one in which the third reaction was irreversible fitted the data (Figure 5), returning the following rate constants: k₁=1.2 s⁻¹, k₋₁=0.3 s⁻¹, k₂=18 s⁻¹, k₋₂=6.5 s⁻¹ and k₃=3.5 s⁻¹.

Figure 5. Representative results of the global fit of absorbance changes and internal aldimine formation.

Top panel: internal aldimine formation (●) and nine kinetic traces (only three of which are shown for clarity in the inset) were fitted by least squares to differential equations corresponding to Scheme 1. Middle panel: expanded view showing the early phase of the reaction. Bottom panel: residuals of the fit relative to all nine kinetic traces and the internal aldimine formation.

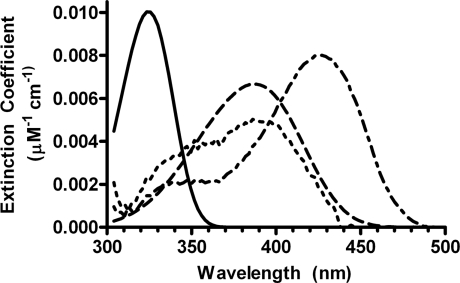
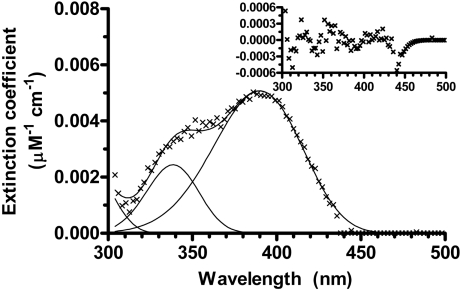
The absorption spectra of the kinetic species, reconstructed from the micromolar absorption coefficients estimated in the fitting, are shown in Figure 6. The spectrum of the intermediate E=PLP* was deconvoluted into its component bands using Metzler's band-shape analysis method (Figure 7) [33]. The main component band has its maximum absorbance at 386 nm. Two additional bands with maxima at 337 and 286 nm respectively had to be included in order to obtain a good fit. The other parameters returned by the fitting were within a ±5% range of the values found in the literature for absorption spectra of PLP-dependent enzymes [34].

Figure 6. Absorption spectra of kinetic species in Scheme 1, as reconstructed from the estimated micromolar absorption (‘extinction’) coefficients yielded by the global fit.

Spectra: ——, apo-E•PLP_Hyd; –––––, apo-E•PLP_Ald;-----, E=PLP*;-·-·-·-, holoE.

Figure 7. Band-shape analysis of the absorption spectrum of the intermediate holoE.

The reconstructed spectrum of E=PLP* (×) was deconvoluted into its component bands (continuous lines) with absorption maxima at 386, 337 and 286 nm. The inset shows the residuals of the fit. Extinction coefficient, micromolar absorption coefficient.

Binding of PNP to apo-eSHMT

Scheme 1 assumes that hydrate PLP binds rapidly to apo-eSHMT. This hypothesis was tested by following the binding of the structural analogue PNP, which cannot proceed further in the reaction sequence because it lacks an aldehyde. PNP does bind to apo-eSHMT, as indicated by the increase of this vitamer's fluorescence emission observed upon mixing with the apoE (results not shown). We calculated a K_d=90±5 nM for this binding equilibrium. Stopped-flow fluorescence experiments in which 2 μM PNP was mixed with excess apoE (60 μM), so as to guarantee pseudo-first-order conditions, gave biphasic kinetics with apparent rate constants of 178±4 and 3.21±0.01 s⁻¹. The linear-dependence of the higher rate constant on protein concentration indicated that it corresponds to the encounter between PNP and apo-eSHMT. The much slower phase that follows is likely to be a conformational change of the enzyme. A k_on of 1.6±0.4 s⁻¹·μM⁻¹ and a k_off of 76±14 s⁻¹ were calculated for the bimolecular step. With 60 μM apoE (as in the rapid-scanning experiments), an observed binding rate constant of approx. 172 s⁻¹ would be measured (k_on×60 μM+76 s⁻¹). This means that binding takes place with a half time of approx. 4 ms, which is not far from the dead time of the stopped-flow instrument (2–3 ms).

DISCUSSION

Second PLP-binding site

The apparent dissociation constants calculated in the binding, inhibition and activation experiments are very similar. This suggests that they are relative to the same binding equilibrium. Lys³⁴⁶, the residue that binds the second PLP molecule, is highly conserved in SHMTs and forms a salt-bridge with the carboxy group of the glutamate residue of H₄PteGlu [35]. PLP binding at this site therefore inhibits the folate-dependent serine-cleavage reaction. The activation of the folate-independent L-allo-threonine cleavage is explained analogously, assuming that PLP binding to Lys³⁴⁶ mimics H₄PteGlu binding. It was indeed reported by Webb and Matthews [36] that H₄PteGlu stimulates the aldol-cleavage reaction. To our knowledge, this second PLP-binding site has not been reported previously. Our discovery was incidental, and we limited its significance to the design of the kinetic experiments.

Proposed mechanism for PLP addition to apo-eSHMT

Before the reaction begins, the free cofactor is present as an equilibrium mixture of hydrate and aldehyde forms (PLP_Hyd and PLP_Ald in Scheme 1). Upon mixing PLP and apoE, a rapid non-covalent binding equilibrium is established in the dead-time of the stopped-flow instrument. Scheme 1 assumes that both hydrate and aldehyde PLP bind rapidly to the apoE. This assumption is well substantiated. The solution rate constant for interconversion of PLP_Hyd and PLP_Ald at pH 7.0 and 25°C has been reported to be approx. 10 s⁻¹ [37]. We found it to be 16 s⁻¹ in the buffer used for our experiments at pH 7.2 and 30°C. This rate constant is not observed in either the single-wavelength or rapid-scanning kinetic results in our binding studies. This suggests that hydrate PLP binds to the enzyme. Moreover, we showed that PNP, a good structural analogue of hydrate PLP, binds rapidly to the apoE.

The rate constants determined for Scheme 1 from the rapid-scanning data compare favourably with those obtained for the single-wavelength studies. The values of k₁, k₋₁, k₂, k₋₂ and k₃ make it clear that the complex of the enzyme with PLP_Ald (apoE•PLP_Ald) reacts much faster than the corresponding complex with the hydrate (apoE•PLP_Hyd). Thus, upon combination of the cofactor with the apoE, the apoE•PLP_Ald complex evolves to the equilibrium species (E=PLP*) before apoE•PLP_Hyd decays to any significant extent. Therefore the apparent rate constants k_a (23.8 s⁻¹) and k_b (3.44 s⁻¹) from the single-wavelength studies correspond roughly to the sum of the intrinsic rate constants k₂+k₋₂ (18 s⁻¹+6.5 s⁻¹) and to k₃ (3.5 s⁻¹) respectively. The slowest exponential process, dominated by k_c (0.53 s⁻¹), represents the decay of apoE•PLP_Hyd, which corresponds to the conversion of the enzyme-bound hydrate PLP (apoE•PLP_Hyd) into the enzyme-bound aldehyde form (apoE•PLP_Ald). Alternatively, it may correspond to the dissociation of hydrate PLP from the enzyme, its dehydration and binding to the apoE as aldehyde.

The absorbance change at 435 nm reports the formation of holoE. There is a pronounced lag in the formation of holoE in the stopped-flow studies (Figure 2, inset). Within experimental error, the rate of the burst in the quench-flow studies (Figure 4) is the same as the lag in the rapid reaction studies. This suggests that holoE is formed from an intermediate aldimine species not absorbing at 435 nm (shown as E=PLP* in Scheme 1).

The spectrum of E=PLP* has a major absorption band with a maximum at 386 nm (Figure 7). Protonated aldimines are normally observed to have maximum absorption between 410 and 430 nm. However, aldimines absorbing between 385 and 400 nm have been reported in the literature [38–40]. In particular, evidence was presented that in the aspartate aminotransferase Y225F mutant at high pH, the chromophore absorbing maximally at 386 nm was the unprotonated internal aldimine [41,42]. In this case, the maximum absorbance of the unprotonated aldimine, usually positioned at around 360 nm, was shifted to higher wavelengths due to the alteration of the active-site environment caused by the mutation. The unusual absorption maximum at 386 nm of the E=PLP* aldimine suggests that the incompletely formed active site of apo-eSHMT may also bind PLP as an unprotonated aldimine. A smaller absorption peak is also observed at 337 nm for E=PLP* (Figure 7). This may be attributed to an enolimine tautomer, or more likely to a required carbinolamine intermediate that is in rapid equilibrium with the aldimine [43].

The final step in Scheme 1 (E=PLP* going to holoE) is most likely to be a conformational change. This step is predicted to be largely irreversible, trapping the PLP in its deep cleft as revealed from its crystal structure. Interestingly, the slower fluorescence change associated with PNP binding to apo-eSHMT takes place with a similar rate constant, suggesting that the final conformational change may be independent from the internal aldimine formation.

Our future studies will be aimed at answering several key questions raised by the proposed mechanism shown in Scheme 1. The first one concerns the structural features that the cofactor requires in order to form the first non-covalent complex with the apoE and then trigger the conformational change that yields the holoE. Do aldimines of PLP with amino acids bind? Does eSHMT bind the aldimines of its substrates glycine and serine selectively with respect to aldimines of non-substrate amino acids? What is the K_d of the first binding equilibrium? Logic would predict that the first complex formed by the apoE with PLP would result in a relatively low K_d, so that PLP would not be sequestered by the cell cytoplasm, where this very reactive aldehyde is subject to reactions with a host of nucleophiles. In the cell there may be little PLP_Ald. Most of it is likely to be present as aldimines with amino acids or complexes with thiol compounds [10]. Studies on PNP binding gave a K_d of approx. 47 μM for the first binding equilibrium of (k_off/k_on).

Other interesting questions relate to the role of Lys²²⁹ in the final conformational change (E=PLP* going to holoE) and the structure of apo-eSHMT. The first one may be answered by studies on site-specific mutants. Folding studies suggest that an N-terminal segment and an interdomain loop that form part of the active site are both exposed to solvent in a folding intermediate that precedes the formation of apo-eSHMT. Maybe these structural elements of the protein are still exposed in apo-eSHMT and E=PLP*.