Scaling metabolic rate fluctuations

Abstract

Complex ecological and economic systems show fluctuations in macroscopic quantities such as exchange rates, size of companies or populations that follow non-Gaussian tent-shaped probability distributions of growth rates with power-law decay, which suggests that fluctuations in complex systems may be governed by universal mechanisms, independent of particular details and idiosyncrasies. We propose here that metabolic rate within individual organisms may be considered as an example of an emergent property of a complex system and test the hypothesis that the probability distribution of fluctuations in the metabolic rate of individuals has a “universal” form regardless of body size or taxonomic affiliation. We examined data from 71 individuals belonging to 25 vertebrate species (birds, mammals, and lizards). We report three main results. First, for all these individuals and species, the distribution of metabolic rate fluctuations follows a tent-shaped distribution with power-law decay. Second, the standard deviation of metabolic rate fluctuations decays as a power-law function of both average metabolic rate and body mass, with exponents −0.352 and −1/4 respectively. Finally, we find that the distributions of metabolic rate fluctuations for different organisms can all be rescaled to a single parent distribution, supporting the existence of general principles underlying the structure and functioning of individual organisms.

Living organisms have been described as the most complex system in the universe, emerging from the activity of an adaptive network of interacting components that allows energy, materials, and information to be acquired, stored, distributed, and transformed (1, 2), and whose end result is the maintenance and reproduction of the network itself (3). A striking feature of complex systems is that they show regularities in the behavior of macroscopic variables, which emerge as the result of nonlinear interactions among multiple components and because of the competition of opposing control forces (4–6). These regularities commonly take the form of simple scaling relationships or power-laws (7, 8). A macroscopic variable that shows scaling relationships is metabolic rate (VO₂) (the rate at which an animal consumes oxygen), which scales with body mass (M) such that VO₂ ∝ M^a with α<1.

For over a century, biologists have documented and tried to explain both the value of α, and the effects ecological factors have on it (1, 9–17). Most of these studies focus on average values of VO₂ and M, and do not consider the temporal variability in individual energy use. However, physiological variables, such as cardiac and breathing dynamics, display complex rhythms, which often show changes both with disease and aging (17–20). In this context, the study of fluctuations in VO₂ can shed light on the determinants of metabolic scaling and provide a way to test competing models and explanations. Indeed, work on complex systems has shown that study of the scaling properties of fluctuations in macroscopic quantities can provide insights on the processes responsible for the macroscopic behavior, even in the absence of detailed mechanistic descriptions of the functioning of the system (4–6). Most comparative analyses of VO₂ variability study circadian rhythms (21–24), and do not examine high frequency variation. In this contribution, we argue that the study of high frequency fluctuations in VO₂ across different species may provide insights on the processes determining its dynamics and their interaction with body size and physiology.

In general terms, the rates of whole-body VO₂ displayed by animals represent the interaction between a supply component, represented by the network that supplies metabolic substrates, removes waste products and regulates activity and a demand component, represented by the sum of cellular respiration rates in various metabolically active organs within the whole organism. Although the relative importance of supply and demand components in accounting for metabolic rate and in particular for the value of the scaling exponent α is still debated (1, 14, 16, 17), it is accepted that to maintain homeostasis, living organisms must allocate their available resources to meet the demands of different organs and their component tissues. This has for long been recognized by physiological ecologists in the context of allocation to generic functions such as growth, reproduction, and maintenance (25, 26). In this regard, the allocation of limited resources to varying functions implies the existence of a complex web of competing forces, which together drive the resultant metabolism. Furthermore, some of the processes involved in the supply of oxygen and its consumption at cellular level are usually driven by competing forces, such as the case of respiratory and cardiac systems, which respond to parasympathetic versus sympathetic stimuli from the autonomic control system (27, 28). These two characteristics, the emergence of a macroscopic phenomenon (in this case whole-body VO₂) from microscopic interactions with a large number of degrees of freedom and the competition of opposing control forces, are hallmarks of complex systems such as those studied in statistical physics and economy (4, 6).

In recent years, Stanley and coworkers (29–31) have studied fluctuations in diverse complex systems, such as business firms, countries, universities, and bird assemblages, and have shown that despite the many striking differences setting them apart, they all show non-Gaussian tent-shaped distributions of growth rates with power-law decay. This has led to the proposition that the fluctuations of complex systems are governed by universal mechanisms, independent of particular details and idiosyncrasies (4, 5, 29, 31). If this is so, this hypothesis should hold true in other complex systems, and thus we should expect the statistical properties of fluctuations in VO₂ of individual animals to follow these universal laws. In this context, we aim to test the working hypothesis that the distributions of VO₂ fluctuations of individual organisms in different species follow a tent shaped distribution. Further, because biological rates, such as breathing or heart rate, scale as M^−1/4 (11, 32, 33), it can be expected that the magnitude of relative fluctuations in VO₂ should decrease with increasing body mass following a −1/4 power. This implies that much of the variability in VO₂ fluctuations can be accounted for by rescaling the original distribution by its observed standard deviation. We thus expect that all distributions, regardless of species, sex, and size will collapse to an universal distribution of fluctuations under rescaling.

Results

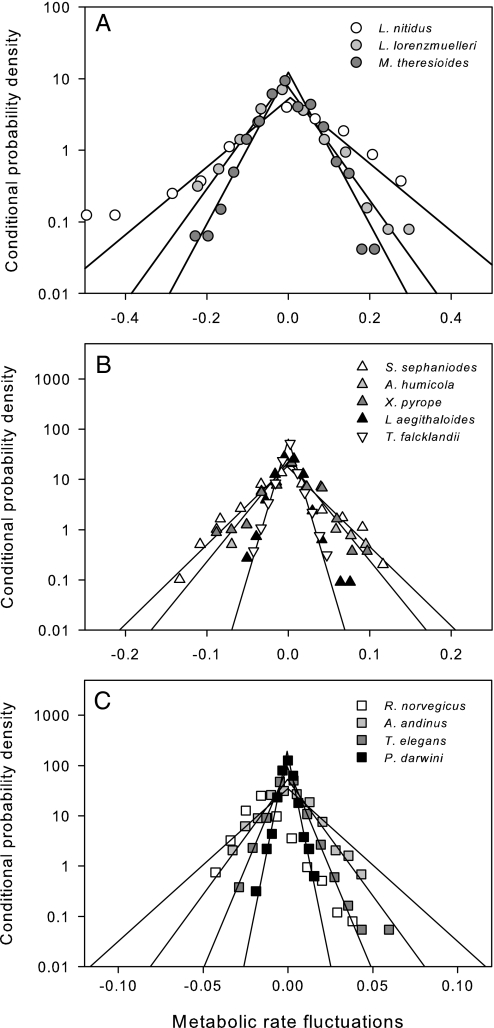
We studied VO₂ time series for 71 individuals belonging to 25 species of small terrestrial vertebrates (10 bird species, 12 small mammals, and 3 lizards) [see supporting information (SI) Table 1]. We found that, for all individuals studied, the conditional probability density of VO₂ fluctuations p(r|v) has a simple “tent” shape, although with different widths. Given that individuals of the same species did not differ greatly in their body sizes, we pooled the information from conspecific individuals, and then compared the distributions of fluctuations between different species (SI Table 2 shows results for individual organisms). Fig. 1 shows the results for a subset of the species we studied. This tent-shaped distribution corresponds to the double exponential or Laplace distribution (29, 34)

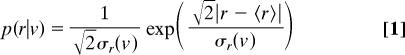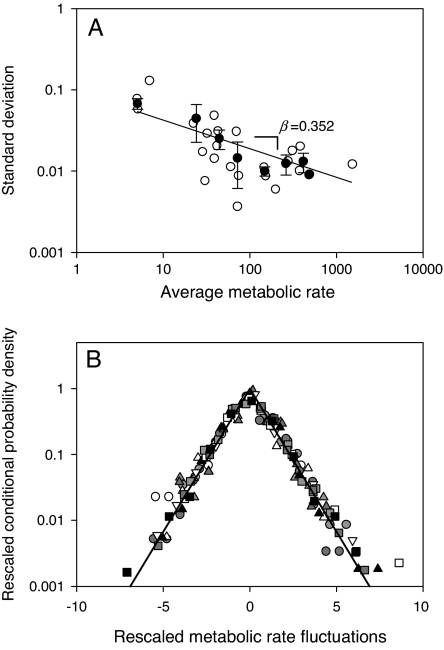
where 〈r〉 and σ_r(v) correspond to the mean and standard deviation of VO₂ growth rates, respectively. A likelihood ratio test statistic (34, 35) showed this fit to be statistically significant for all of the species studied and different from a Gaussian distribution, which is to be expected if system components vary independently of each other (see SI Table 3 for tests results at the species level). In agreement with this result the variation in the width of the distribution of the VO₂ growth rates, measured by its standard deviation σ_r(v), is a function of 〈VO₂〉, the average rate of oxygen consumption. Fig. 2A shows that despite residual variation in the data, σ_r(v) scales as a power-law

with an exponent β = −0.352 ± 0.072 (ordinary least squares regression estimate ± 1 SE, 95% confidence interval: −0.208 to −0.496). On the other hand, σ_r(v) scales with body mass as

with γ = −0.241 ± 0.103 (ordinary least squares regression estimate ± 1 SE, 95% confidence interval: −0.035 to −0.447), which does not differ from the expected −1/4 exponent.

Fig. 1.

Fluctuations of metabolic rate in terrestrial vertebrates. (A) Conditional probability density function p(r|v) of the growth rates r in three lizard species. (B) Conditional probability density function p(r|v) of the growth rates r in five bird species. (C) Conditional probability density function p(r|v) of the growth rates r in four small mammal species. For all three figures, the solid lines are fits to Eq. 1, using the mean 〈r〉 and standard deviation σ_r(v) calculated for the data from each species.

Fig. 2.

Scaling and universality of metabolic rate fluctuations. (A) Filled circles show average standard deviation σ_r(v) of observed metabolic rate fluctuations as a function of average metabolic rate 〈VO₂〉. The solid line shows a least squares regression fit to the log transformed data, with slope β = 0.325 ± 0.07. Error bars show one standard error. Also shown in open circles are the data observed for each species. (B) Scaled probability density function $p_{scal}\text{=}\sqrt{\text{2}}{\sigma }_r(V)p(r|V)$ plotted against the scaled growth rate $r_{scal}=\sqrt{2}\left[r-\langle r(V)\rangle \right]/{\sigma }_r(V)$ for all of the species shown in Fig. 1. Note that the scaled data collapse onto the single scaling curve p_scale = exp(−|r_scal|)

All these species show the same scale invariant probability distribution of VO₂ fluctuations, regardless of the differences in their phylogeny, physiology, and body size, which suggests that they are expressions of a more general phenomenon. If this is indeed the case, we expect these distributions to show data collapse under adequate rescaling (29, 31). Fig. 2B shows that when we plot the scaled probability density function $p_{scal}\text{=}\sqrt{\text{2}}{\sigma }_r(V)p(r|V)$ against the scaled growth rate $r_{scal}=\sqrt{2}\left[r-\langle r(V)\rangle \right]/{\sigma }_r(V)$, the observed distributions for all of the species do indeed collapse, with data from all of the species converging onto a single scaling curve p_scal = exp(−|r_scal|).

Discussion

Our results show that the distribution of metabolic rate fluctuations follows a tent-shaped distribution rather than the normal distribution expected from the null model of a random multiplicative process. This is not so surprising if one considers that such a null model implies that log(VO₂) follows a random walk, and hence is not regulated. However, metabolic rate is under homeostatic regulation and must show dynamic feedback structure. A simple dynamical model showing such a feedback is the biased random walk,

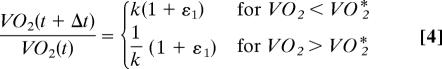where k is a constant >1, measuring the strength of the feedback input biasing the random walk toward a preferred value, and ε_t are uncorrelated Gaussian random numbers with zero mean and variance σ_ε² ≪ 1. For this well studied problem, r is distributed according to Eq. 1 (29). Extensions of this model that include more than one scale of regulation have been shown to generate complex dynamics similar to those observed in other physiological variables (36). Thus, the nonnormality of VO₂ fluctuations provides evidence of homeostatic regulation or feedbacks acting on VO₂.

It has been argued the tent-shaped distributions of growth rates in complex systems may emerge if the units composing the system evolve according to a random multiplicative growth process (e.g., a mixture of lognormal distributions with different variances) (37, 38). However, for this explanation to hold in our system, the amount of oxygen consumed by the units composing the system (i.e., cells, tissues or organs) would need to be independent, with similar mean and different variances. Notwithstanding that the assumption of independent energy use is likely a strong one (see below), considering that energy is usually limited and its allocation to different functions (growth, storage, and reproduction) and trade-offs have fitness consequences (39) we cannot at present provide a definitive test of this explanation, because such a test would require the availability of measurements of metabolic rate dynamics at the level of cells, tissues, and organs within living organisms. Further research on the statistical patterns of VO₂ dynamics within individuals and across different species are needed to gain a better understanding of the nature of the homeostatic processes acting on this emergent attribute of individual organisms.

Our second result is the power-law decay of the width of the distribution p(r|v) as a function of both average metabolic rate and body size. The simplest model to explain the dependence of σ_r(v) on 〈VO₂〉 would be to assume that an organism is made up of n equally sized cells of mass m_c, each consuming oxygen at independent rates. The central limit theorem predicts σ_r(v) decays as n^−1/2 or equivalently under this general assumption, as M^−1/2 (37, 40). If 〈VO₂〉 is assumed to be proportional to n, we would also expect that σ_r(v) ∝ 〈VO₂〉^−1/2. However, the decay in VO₂ fluctuations is much slower, and both β and γ are >−1/2 (β = −0.352 ± 0.072 SE and γ = −0.241 ± 0.103 SE), which suggests that cellular oxygen consumption rates are not independent within an organism, further reinforcing the existence of physiological feedbacks, which do not fully synchronize all cells. On the other hand, if all cells were strongly correlated, then the size of the organism should not matter, and we should find that β = γ = 0. Interestingly, it can be shown that the scaling of VO₂ fluctuations is related to the more widely studied allometric scaling of VO₂ by the following expression: γ = α × β. This predicts a value of γ = −0.27 ± 0.14 SE, which does not differ from the observed −1/4 value. Future research may be directed to examining whether dynamical extensions of existing explanations of the allometry of VO₂, either the supply limitation (1) or the multiple control model (16) can predict statistical patterns in VO₂ variability.

In closing, we want to emphasize that individual organisms are complex systems, the study of which could provide the basis for a deeper understanding of complex ecological and economic systems, which, unlike individuals, do not allow for controlled experimentation. The universality of tent-shaped distributions for VO₂ fluctuations across individuals belonging to species that differ in many regards, including the details of their respiratory system, their thermal physiology, and body size, supports the claim that complex biological systems show power-law dependence in emergent quantities, the same as do other physical and economic systems. Reconciling or resolving the apparent contradiction between such universal patterns and the observed diversity of form and function in animal taxa is an emerging challenge for scientists working at the interface between evolutionary biology, physiology, and complex systems sciences.

Materials and Methods

Determination of Individual Metabolic Rate.

To study the scaling properties of metabolic rate fluctuations, we recorded VO₂ time series for individual organisms at rest during observation periods averaging 1 h. To determine VO₂, we transferred individuals of different species of small terrestrial vertebrates (mammals, birds, and lizards) to the laboratory and housed them individually. VO₂ was determined according to the following protocol for measurements collected over a 3-h period during midmorning: Birds were measured in dark metabolic chambers. Oxygen consumption was measured in a Datacan V computerized open-flow respirometry system (Sable Systems, Henderson, NV). The metabolic chamber received dried air at a rate ranging from 500 to 1,000 ml/min from mass flow-controllers (Sierra Instruments, Monterey, CA), which ensured adequate mixing in the chamber. In all cases, the metabolic chambers allowed the animals a limited amount of movement. It is important to note that, although these movements could potentially increase the observed metabolic rate, all measurements were done in the rest phase of the circadian cycle of these species. Air passed through CO₂ and H₂O absorbent granules of Baralyme and Drierite respectively before and after passing through the chamber and was monitored every 5 s by an Applied Electrochemistry O2-analyzer, model S-3A/I (Ametek, Pittsburgh, PA).

Birds and mammals were fed ad libitum with bird seed and rabbit food pellets respectively, and lizards were fed mealworms (Tenebrio molitor). Water was also provided ad libitum. Ambient temperature (Ta) and photoperiod were held constant at 20 ± 2°C and 12:12 light:dark. Animals were held for 1 and 2 days before VO₂ measurements and then fasted for 6–12 h. before placement in metabolic chambers, at Ta within the thermoneutral zone of each endothermic species (41–43). Standard metabolic rates of lizards were measured at Ta = 30°C. Individual body size was measured by using a digital balance at the beginning and at the end of each experiment. All experiments with animal subjects were conducted according to current Chilean law for ethical manipulation of laboratory animals and under permits issued from Servicio Agrícola y Ganadero.

Data Processing and Analysis.

To study the statistical properties of fluctuations in VO₂, we examine its variation within a single organism during a given period (averaging 1 h of observation). The fluctuations of a variable may be described by many quantitative descriptors, such as their periodicity, amplitude, and frequency spectrum (44). However, as a first approximation, we choose as our measure of variability the growth rate of VO₂ in logarithmic scale, and so we define r ≡ log[VO₂(t+τ)/VO₂(t)], where VO₂ (t) and VO₂ (t + τ) are the metabolic rates observed for a given individual in time intervals t and t + τ, respectively. This measure has the advantage that it removes the effect of any trends and hence is not affected by changes in the average value of the variable (6). We also define v = log[〈VO₂〉], the logarithm of the average metabolic rate observed over the study period. We then calculate the conditional probability density distribution, p(r|v), of growth rates r for each species with a given v.

The simplest model for the fluctuations in VO₂ is one that assumes that it fluctuates independently of organism size and that successive fluctuations are uncorrelated in time. These assumptions can be formalized in a simple random multiplicative process, which predicts that VO₂ values should be log-normally distributed (28). A direct consequence of this is that p(r|v) follows a Gaussian distribution, which would show in our graphs as a parabola. We take this as our null hypothesis for the fluctuations of VO₂. On the other hand, studies on other complex systems have shown that p(r|v) can be described by a Laplace distribution (Eq. 1) (28–30, 34, 37) Therefore, for each of the species studied, we tested the hypothesis that the conditional probability density p(r|v) fits either a Laplace or a Gaussian distribution, using a likelihood ratio test statistic (see refs. 34 and 35 for details).

If the conditional probability density functions of different individuals or species follow the same functional form, one would expect that under a nontrivial scale, transformation that all of these distributions should converge or collapse into a single statistical distribution. By “scaling,” we mean applying the same function of observed parameters to the distributions. If the scaling holds, then, data for a wide range of parameter values [in this case, values of v and σ_r(v)] are said to “collapse” on a single curve. One key parameter in the rescaling procedure is the width of the conditional distribution p(r|v). It can be expected that the magnitude of fluctuations should decrease with increasing body mass following a −1/4 power (11, 45, 46), so that VO₂ in smaller individuals should fluctuate more in than large ones. The magnitude of the variability or fluctuations in a variable can be measured by examining the standard deviation of growth rates, σ_r(v). Thus, we also examined the possible effects of average metabolic rate and body size on the magnitude of VO₂ fluctuations as measured by the value of σ_r(v) by plotting the scaling relationship between these two variables. Given the low measurement error rate in both body size (47) and VO₂, we estimated the scaling exponent, using ordinary least squares regression.

Abbreviations

VO₂

metabolic rate (ml O₂/h)

M

body size (g).