Step Length Measurement—Theory and Simulation for Tethered Bead Constant-Force Single Molecule Assay

Abstract

Linear molecular motors translocate along polymeric tracks using discrete steps. The step length is usually measured using constant-force single molecule experiments in which the polymer is tethered to a force-clamped microsphere. During the enzymatic cycle the motor shortens the tether contour length. Experimental conditions influence the achievable step length resolution, and ideally experiments should be conducted with high clamp-force using slow motors linked to small beads via stiff short tethers. We focus on the limitations that the polymer-track flexibility, the thermal motion of the microsphere, and the motor kinetics pose for step-length measurement in a typical optical tweezers experiment. An expression for the signal/noise ratio in a constant-force, worm-like chain tethered particle, single-molecule experiment is developed. The signal/noise ratio is related to the Fourier transform of the pairwise distance distribution, commonly used to determine step length from a time-series. Monte Carlo simulations verify the proposed theory for experimental parameter values typically encountered with molecular motors (polymerases and helicases) translocating along single- or double-stranded nucleic acids. The predictions are consistent with recent experimental results for double-stranded DNA tethers. Our results map favorable experimental conditions for observing single motor steps on various substrates but indicate that principal resolution limits are set by thermal fluctuations.

INTRODUCTION

Helicases and polymerases are linear molecular motors that translocate along a variety of nucleic acids (NA). Significant insight into the working of these motors has been gained from single molecule experiments (1–6). In particular, optical tweezers have been instrumental in delineating the mechanisms of RNA polymerase (7,8) and RecBCD helicase (9,10). Recent developments in optical trapping technology have suppressed instrumental noise and drift to a level that permits measuring RNA polymerase translocation with single base (∼0.3 nm) resolution (8). In contrast to other linear molecular motors, like kinesin and myosin, the NA tracks of helicases and polymerases are flexible, with persistence lengths (L_p) ranging from <1 nm for single-stranded (ss) NAs (11) to 50 nm for double-stranded (ds) NAs (12,13). In comparison, actin filaments and microtubules are stiffer (L_p > 10 μm) (14), and often rigidly immobilized in single-molecule stepping assays. Immobilization of the NA track is precluded for motors that topologically enclose the NA during translocation. Thus, the flexibility of the NA chain, especially in the case of ssNA, needs to be taken into account in optical tweezers experiments. While recent experimental results have provided a set of favorable experimental conditions for observing steps down to single basepair resolution on dsDNA, no steps have yet been resolved for motors that move along single-stranded substrates. Many replicative DNA and viral RNA polymerases fall into this motor category (15–21). In addition, single-strand translocation is a common activity of helicases (22) and viral RNA packaging motors (23).

A typical optical tweezers experiment involving an NA-translocating motor is performed by observing a trapped handle (∼1 μm diameter polystyrene or silica bead) tethered through the motor and the bound NA to a stationary sample chamber or another trapped bead (8,12).The motor can be bound to either end of the NA, and its enzymatic cycle results in a successive reduction of the NA contour length with a step size characteristic of the motor. However, in experiments performed under physiological conditions, thermal fluctuations of the microsphere due to the flexible NA limit the achievable spatial resolution (24). Thus, to take full advantage of sub-nanometer resolution instrumentation (8,25,26), an understanding of the experimental conditions under which a given step length can be measured is needed. A recent study has assessed the detection of steps in the so-called dumbbell configuration by analyzing correlated motions of the two trapped handles (25). Here we focus on the one-handle, surface-immobilized configuration, which is preferred when simultaneous detection of single-molecule fluorescence is desired (27).

We present a theoretical assessment of the signal/noise ratio (SNR) for a motor step-size measurement in a model optical tweezers experiment (Fig. 1). The idealized motor shortens the tether contour length in discrete steps of uniform length at a given average rate. The tether is modeled as a worm-like chain (WLC). A simple approximate formula for the SNR is also derived from the theory. The theory is verified by Monte Carlo simulations for a range of plausible experimental parameters (force-clamp set point, microsphere diameter, molecular motor step length, stepping rate, and WLC contour/persistence length) relevant to the study of NA translocating molecular motors (Table 1). From the simulations, the minimum SNR at which steps can be measured is predicted. The proposed theory is consistent with the limits observed in recent high-resolution experimental studies on dsDNA motors (8,28). The theory enables predicting SNR for ssNA motors and yields a set of favorable experimental conditions under which short steps can be detected, while exposing the intrinsic limitations of the assay.

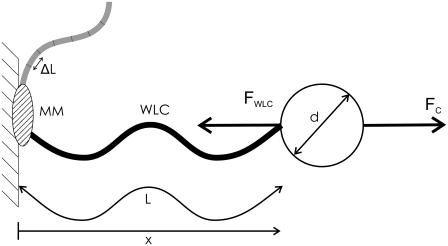
FIGURE 1.

Model for single-molecule motor experiment. A microsphere (diameter d) is tethered to a stationary sample chamber by an NA modeled as a worm-like chain (WLC) with contour length L, end-to-end distance x, and persistence length L_p. The effect of a molecular motor (MM) is modeled by successively shortening the contour length of the WLC by an amount ΔL, the molecular motor step length. The microsphere is held in a force-clamp with a constant pulling force F_C, balanced by the counter-force F_WLC.

TABLE 1.

Input parameters used for simulations

Parameter	Range
Step length ΔL	0.3–6 nm
Step rate kcat	10–1000 s−1
Contour length L	0.1–10 μm
Persistence length Lp	1–100 nm
Microsphere diameter d	0.1–10 μm
Clamp force FC	1–50 pN
Detection bandwidth	100 kS/s sampling followed by low-pass filtering at fLP = kcat

THEORY

The motion of a micron-sized particle of diameter d, with negligible inertia, in a viscous fluid (viscosity η), tethered to a stationary object by a WLC polymer with contour length L and persistence length L_p, (Fig. 1), is described by the Langevin equation (29),

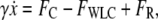(1)

where 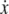is the particle velocity, γ is the hydrodynamic drag coefficient (we use the Stokes formula γ = 6πη(d/2) throughout this article), F_C is the constant clamp-force imposed by the optical tweezers, and F_WLC is the restoring force of the WLC tether. The random thermal force F_R is modeled as white noise with a constant power spectral density of 4 k_BTγ.

The WLC model describes the equilibrium force-extension relationship for dsDNA(12), ssRNA(30), and dsRNA(13) well, but accurate modeling of ssDNA may require use of the modified freely-joined chain model (31). To apply the theory presented here to ssDNA, the force-extension curve can be approximated locally in a limited force region with a WLC model. Here we consider only the equilibrium WLC model, since the time constant for longitudinal relaxation of long dsDNA molecules is ∼10⁻³ s (32), one-to-two orders-of-magnitude faster than the step rate for typical molecular motors.

Due to ease of computation, we use the approximation for the WLC force-extension relationship of Marko and Siggia (33):

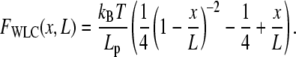(2)

where L_p, L, and x are the persistence length, the contour length, and end-to-end distance, respectively.

As the force clamp is applied the particle relaxes to an equilibrium position x_e, where

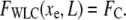(3)

To derive an expression for the SNR we first consider noise, i.e., position fluctuations of the bead around this equilibrium (24). Expanding Eq. 2 into a Taylor series around x_e, and retaining only the first-order term, Eq. 1 can be rewritten as

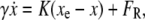(4)

where

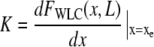(5)

is the effective stiffness of the system, determined by the elasticity of the WLC. Since F_R is a random variable with a white-noise spectrum, its variance can be calculated as the integral of the noise power within the given observation bandwidth f_LP (34). The square-root of the variance, the root mean-square (RMS) of F_R, is thus

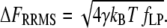(6)

This force uncertainty results in bead position noise

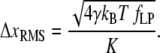(7)

We next consider the magnitude of the position signal produced by an active molecular motor. One enzymatic cycle of the motor results in a decreased WLC contour length L₀−ΔL, where L₀ and ΔL are the original contour length and the step length, thus increasing both the extension of the WLC and the restoring force F_WLC. This produces a change (signal) Δx_e so that a new equilibrium is established where F_WLC (x_e + Δx_e, L₀−ΔL) = F_C. To first-order, this is achieved when

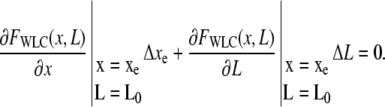(8)

Using Eq. 2, this simplifies to

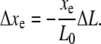(9)

Thus a step measurement will yield a measured step length Δx_e, which is attenuated by the nondimensional extension of the chain 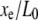compared to the true step length ΔL. The (amplitude) SNR is defined as the ratio of the signal, Eq. 9, to the noise, Eq. 7, as

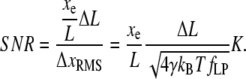(10)

The effect of step length, drag coefficient, and measurement bandwidth on SNR is readily seen. However, from this expression it is not apparent how the SNR behaves as a function of force, WLC contour length, or WLC persistence length, since these affect both x_e and K. Using the root formulas for cubic equations to solve Eq. 3, the equilibrium extension can be found, and substituted into Eq. 5 to obtain the local stiffness. However, these long explicit expressions offer little additional insight into how to design an experiment. To derive a simpler SNR expression from which quantitative SNR estimates in a variety of conditions can be obtained, we analyze the nondimensional WLC model,

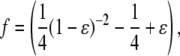(11)

where 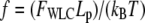is the nondimensional force, and 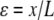is the nondimensional extension. By examining the nondimensional extension (Fig. 2 A) and stiffness 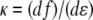(Fig. 2 B) as a function of f, we find approximate expressions for ɛ and κ. In the low force region (I in Fig. 2 A) below f ≈ 0.2, extension increases linearly with force. In the intermediate force region (II in Fig. 2 A) between f ≈ 0.2 and f ≈ 12, extension increases logarithmically with force. Finally, in the high force region (III in Fig. 2 A) above f ≈ 12, extension is a polynomial function of force. Similarly, stiffness is approximated well by an exponential function of f up to f ≈ 2, and by a polynomial for higher forces. These approximations are accurate to within ±10% of the exact solutions, and should thus allow estimating SNR with ±20% accuracy. The simplified expressions for the SNR are

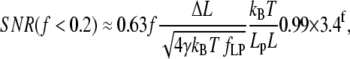(12)

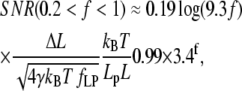(13)

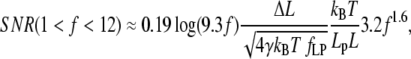(14)

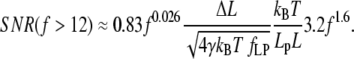(15)

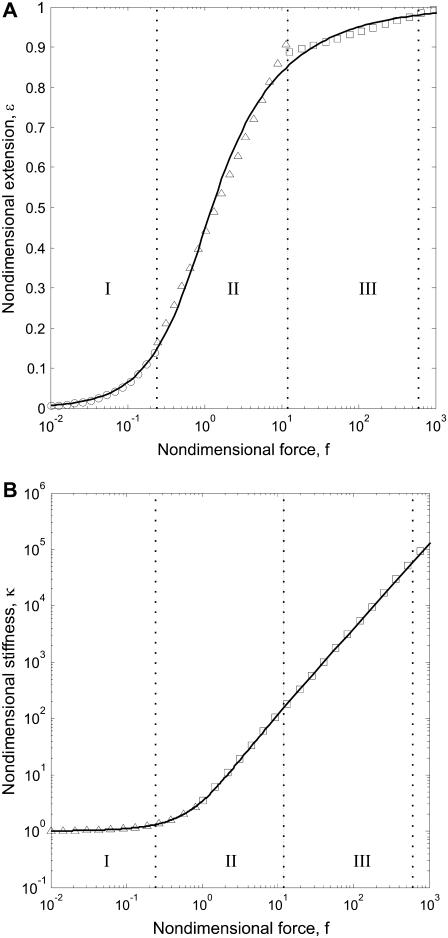
FIGURE 2.

(A) Extension as a function of force for the nondimensional WLC model. The solid line indicates an exact solution to Eq. 3. Circles, triangles, and squares indicate exponential, logarithmic, and polynomial approximations, respectively. Each approximation is accurate to ±10% in its force region, indicated by dotted lines. (B) Nondimensional stiffness as a function of force. The solid line is calculated from Eq. 5. Triangles and squares indicate linear and polynomial approximations, respectively. Force regions as in panel A. Typical experimental forces of between 1 and 50 pN correspond to the high force range (III) for a WLC with L_p = 50 nm (dsNA), and to the medium force range (II) region when L_p = 1 nm (ssNA).

Since temperature is seldom changed by >10% in experiments with biological macromolecules, the persistence length and the clamp-force essentially determine the nondimensional force range. Using two model cases, one with L_p = 1 nm and one with L_p = 50 nm (corresponding to ssNA and dsNA, respectively), and forces from 1 pN and up, we compare these approximations to the exact solution, Eq. 10, in Fig. 3. We find good agreement, and note that steps are likely to be detected only in the medium or high force regions, since SNR ≪ 1 in the low force region. We therefore restrict further discussion of the approximate expressions to the high and medium force range (f > 0.2).

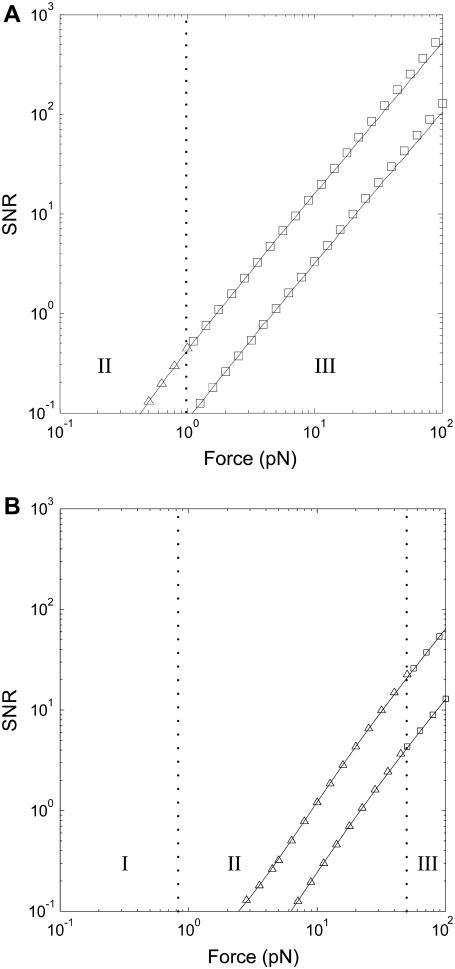
FIGURE 3.

The simple SNR formulas (symbols, Eqs. 13–15) approximate the exact SNR (solid line, Eq. 10) well. The SNR for detecting steps in an experiment with a 1-μm diameter bead in water at room temperature (T = 300 K, η = 1 mPas) and a 100 Hz bandwidth is shown. WLC contour length was 1 μm, and two cases are shown: L_p = 50 nm (A) and L_p = 1 nm (B), corresponding to dsNA and ssNA, respectively. The upper and lower curves are the SNR for detecting a 1.5 nm and a 0.3 nm step, respectively. Symbols correspond to the force regions as in Fig. 2 A: squares in the high force region (III), Eq. 15, and triangles in the medium force region (II), Eqs. 13 and 14.

SIMULATION AND TIME-SERIES ANALYSIS

Numerical simulations of the experiment shown in Fig. 1 were done: 1), to determine a threshold SNR, above which steps can be detected; and 2), to assess the validity and limitations of the approximations used in the derivation of the approximate SNR formulas, Eqs. 12–15.

In our simulations, Eq. 1 was solved numerically using the Euler method (35). The position x_i of the bead at time step i is related to the position x_i−1 at the previous time step i−1 by

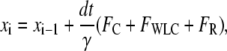(16)

where we use an integration time step dt, and the Stokes formula γ = 6πη(d/2), in which η and d are the dynamic viscosity of the surrounding medium and the bead diameter, respectively.

The enzymatic cycle of a molecular motor is modeled as a successive stochastic shortening of the WLC contour length by an amount ΔL for each step. The distribution of dwell times between steps is exponential, with a time-constant of 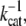corresponding to a mechano-chemical transition of the molecular motor with a constant probability per unit time, and average rate k_cat.

A suitable simulation time step, dt = 0.1 μs for all simulations, was found empirically by decreasing dt until further decrease resulted in negligible change in Fourier transform of the pairwise distance distribution (FTPWD). This time step corresponds to, on average, 10⁴ simulation time steps during the shortest investigated dwell time between molecular motor steps (k_cat = 1000 s⁻¹). The simulation code was written in MatLab (Ver. 7), with CPU-intensive subfunctions implemented in C.

We extract a step length from the simulated time-series by analyzing the periodicity of the pairwise distance distribution (PWD). The position of a peak at a particular spatial frequency in the FTPWD corresponds to the step length in the time-series.

To relate predicted SNR values (Eq. 10) to the height of observed peaks in the FTPWD obtained by simulation, we analyze an idealized time-series. The PWD of an infinitely long time-series of spatial jumps with a fixed step size ΔL, modulated by normally distributed noise of RMS-amplitude Δx_RMS, can be written as a convolution (⊗) (29),

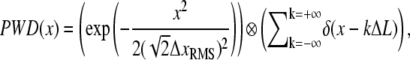(17)

where the first term is the distribution of distances between any two points in the time series, and δ is the delta function. Thus the PWD is a sum of Gaussians with variance 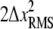placed along the x axis at intervals of ΔL. Any normalizing prefactor is irrelevant for the following analysis and is omitted for simplicity. The Fourier transform of Eq. 17 is

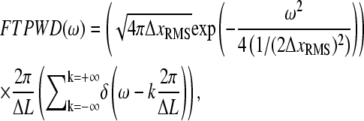(18)

where ω is the spatial frequency. This FTPWD consists of a sequence of peaks modulated by a Gaussian envelope. The peak that corresponds to the step of length ΔL is found at 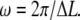Steps are resolved when this peak is discernible in the FTPWD. We designate the normalized height of this peak step detectivity (SD):

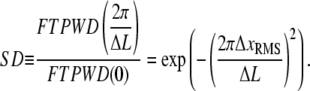(19)

This ratio is independent of PWD counting statistics and normalization, and serves as a numerical indicator of when steps can be resolved. Substituting SNR for 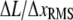(Eq. 10), SD is readily related to the theoretically derived SNR,

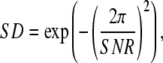(20)

or conversely,

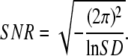(21)

This expression allows us to analyze the FTPWD of a time-series, obtain the SD, and calculate the corresponding SNR, which can be compared to the theoretically predicted exact, Eq. 10, or approximate, Eqs. 12–15, SNR.

Here, for simplicity, we have analyzed an infinite time-series. A finite experimental FTPWD will exhibit broader peaks (the Fourier transform of a finite sum in Eq. 17 is the sinc function). While the finite time-series should not affect the SNR or the obtained FTPWD peak-height (SD), it may degrade the precision with which the peak position (step length) is determined. We have examined the effect of a finite duration experiment on the SD calculation using simulation, as described in Results.

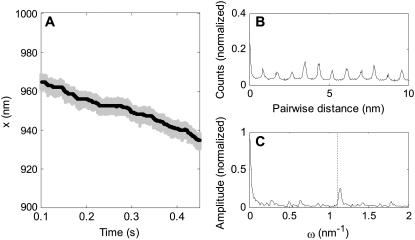
To calculate the SNR using Eq. 21, time-series obtained by simulation were analyzed as follows. First, to account for the finite experimental detection bandwidth of typical optical tweezers instruments (36,37), the solution of Eq. 1 was sampled at a sampling frequency of 100 kS/s (shaded line, Fig. 4 A). Second, to increase the SNR the detection bandwidth was reduced to f_LP = k_cat by low-pass filtering, and to reduce the CPU-time required for the PWD calculation the signal was then resampled at 100 k_cat S/s (solid line, Fig. 4 A). Third, the PWD was calculated and normalized (Fig. 4 B). Fourth, the FTPWD (Fig. 4 C) was calculated (no windowing was used) and the normalized height (SD) and position of any peak near 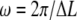was found using a peak-search algorithm.

FIGURE 4.

(A) Typical simulated time-series (sampled data in shaded, filtered in solid representation). (B) Pairwise distance distribution (PWD) for the filtered data in panel A. (C) Fourier transform of the pairwise distance distribution (FTPWD) in panel B. Note that due to step attenuation, the peak in the FTPWD is displaced toward a higher spatial frequency compared to the frequency corresponding to ΔL (dashed line).

Using this protocol, the SNR was mapped for a range of typical experimental parameters (Table 1) by performing numerous simulations. The step lengths and rates were chosen to correspond to those proposed or observed for polymerases or helicases. The WLC contour lengths correspond to 0.3–30 kb tethers, commonly used for single molecule experiments. The WLC persistence lengths were chosen to span the stiffness range of NA substrates, ranging from ssRNA (L_p > 1 nm) to dsDNA and dsRNA (L_p > 50 nm). The bead size and clamp-force were varied to cover ranges typically used in experiments. An aqueous solution at room temperature was assumed in all simulations (T = 300 K, η = 1 mPas).

RESULTS

Measuring step length requires >20 steps at SNR > 4

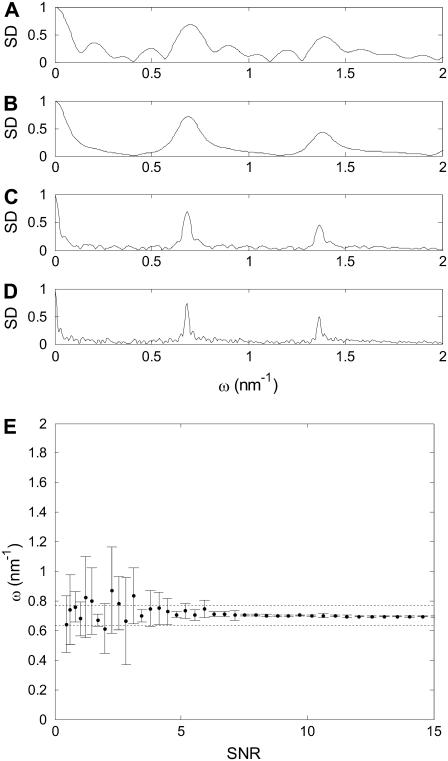
To investigate the minimum required experiment duration, simulations of variable length ranging from, on average, 10 to 100 motor steps were performed. The results show that an experiment encompassing 20 steps or more is sufficient to determine the step length with a precision of ±10% (Fig. 5, A–D). Fewer steps obviously suffice at high SNR when step length can be determined from the time-series directly, and no further analysis is required. A step detection threshold, defined as the minimum SNR at which the step length could repeatedly be correctly (±10%) determined, was established as SNR ≥ 4 by comparing multiple simulations with different SNRs (Fig. 5 E).

FIGURE 5.

(A–D) FTPWD graphs when analyzing time-series with different number of steps, to determine the influence of time-series length on the SD and the determined step length. A short time-series (five steps, A) results in multiple broad peaks. The false peaks are absent in the curve for 10 steps (B), but the main peaks remain broad. A time-series of 20 steps (C) shows well-defined peaks that allow step-length determination with 10% accuracy. Further lengthening the time-series (40 steps, D) improves step length measurement only little. All FTPWD curves show roughly equal SNR (the peaks are equally high). (E) Measured step length as a function of SNR. The average and standard deviation of the determined step length from 10 simulations is shown. Step length can be accurately determined when SNR ≥ 4. Dashed lines correspond to step lengths of 90 and 110% of the true (corrected for attenuation) step length.

General notes on SNR: step length, contour length, bead diameter, and step rate

Examining the approximations in the different force regions, Eqs. 12–15, we find that the SNR is of a form

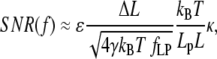(22)

where only the approximations for the nondimensional extension ɛ and stiffness κ change with force region. We note that step length, bead diameter, step rate, and contour length all appear in identical form in these expressions. Predictably, SNR is proportional to step length ΔL. A doubling of step length is required to double SNR. Similarly, SNR is inversely proportional to contour length; a doubling in SNR is obtained by halving L. Bead diameter and step rate have a less direct effect on SNR. A fourfold decrease in either d or f_LP is required to double SNR. Below we consider force and persistence length effects on SNR in the medium and high (nondimensional) force regions. Note that the effect of temperature cannot be assessed from Eq. 22 alone, because ɛ, κ, and γ (through viscosity) are functions of temperature. But since temperature usually cannot be varied by >±10% for most biological experiments, we do not consider it in detail here.

SNR in the medium force region (0.2 < f < 12)

Two approximations, above and below f = 1, must be considered in this force region (Eqs. 13 and 14). The lower region, where 0.2 < f < 1, applies when 0.8 pN < F < 4 pN, if L_p = 1 nm (ssNA), and 0.02 pN < F < 0.08 pN if L_p = 50 nm (dsNA). In this region SNR can be approximated by

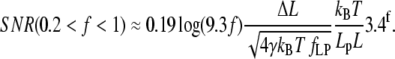(23)

For higher forces, 1 < f < 12, applicable when 4 pN < F < 50 pN, if L_p = 1 nm (ssNA), and 0.08 pN < F < 1 pN if L_p > 50 nm (dsNA), SNR can be approximated by

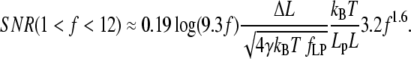(24)

In these expressions, the effect of force on ɛ is best read from Fig. 2 A, due to the logarithmic dependence on f. The nondimensional extension ranges from 0.1 to 0.8, and thus has a dramatic effect on SNR. The effect of force on nondimensional stiffness is more readily expressed quantitatively (Fig. 2 B): In the lower range (0.2 < f < 1), an increase of 0.56 (nondimensional units) in f is required to double SNR. In the upper range (1 < f < 12), a 1.54-fold increase in f doubles SNR. Here we have stated our results in terms of the nondimensional force, since the effect of force and persistence length on SNR is difficult to decouple in Eqs. 23 and 24.

SNR in the high force region (f > 12)

The high force region is applicable above F = 50 pN when L_p = 1 nm (ssNA), and above F = 1 pN when L_p = 50 nm (dsNA). In this region SNR can be approximated by

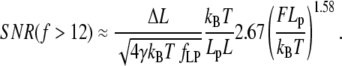(25)

We note that a 3.3-fold increase in persistence length is required to double SNR. Force, on the other hand, affects SNR strongly: a 1.55-fold increase in force doubles the SNR.

Comparing simulation to theory

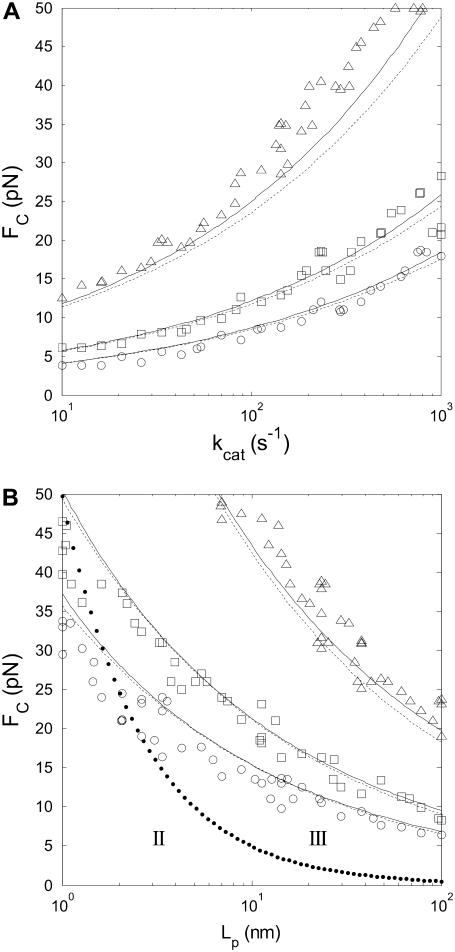
To verify the predictions for how each parameter (step length, step rate, bead diameter, WLC contour- and persistence length, and force) affects SNR, we compared SNR values obtained by analysis of simulated time-series to predicted SNR (Eq. 10 and 25). The dependence of the SNR on all six parameters is hard to visualize in one figure, so we chose to plot the SNR threshold for step detection as a function of two parameters at a time, with force on the y axis. Fig. 6 A shows results when varying the step length. Fig. 6 B verifies that the measured step is attenuated according to Eq. 9. Fig. 7 shows SNR threshold contour results when varying the step rate (Fig. 7 A) and the WLC persistence length (Fig. 7 B). Fig. 8 shows SNR threshold contour results when varying the bead diameter (Fig. 8 A) and the WLC contour length (Fig. 8 B). Symbols show threshold SNR contours extracted from analysis of simulated time-series data. Solid lines show the predicted location of the SNR threshold (SNR = 4) from Eq. 10. Dashed lines indicate the SNR threshold derived from the high-force approximation, Eq. 25.

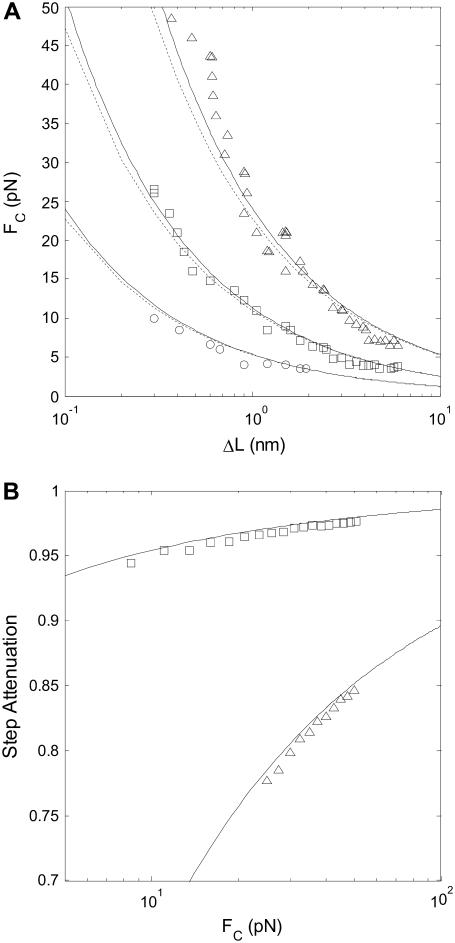
FIGURE 6.

(A) SNR is inversely proportional to step length ΔL. Simulated step detection threshold contours (SNR = 4) as a function of F_C, for step lengths ΔL = 0.3–6 nm at different stepping rates: k_cat = 10 s⁻¹ (triangles), k_cat = 100 s⁻¹ (squares), and k_cat = 1000 s⁻¹ (circles). Solid lines indicate step detection thresholds calculated from the exact formula, Eq. 10, and dashed lines indicate the SNR threshold calculated from the approximate formula, Eq. 25. L = 1000 nm, L_p = 50 nm, and d = 1000 nm. (B) Measured step lengths are attenuated by the nondimensional extension of the WLC. Step attenuation (ratio of measured to true step length) as a function of F_C, for persistence lengths of L_p = 50 nm (squares) and L_p = 1 nm (triangles). The measured step length was determined from the spatial frequency of a peak in the FTPWD. Lines indicate theoretical prediction, Eq. 9.

FIGURE 7.

(A) SNR is inversely proportional to the square-root of the measurement bandwidth f_LP, and proportional to 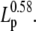Simulated step detection threshold contours (SNR = 4) as a function of F_C for stepping rates between 10 s⁻¹ and 1000 s⁻¹, and (B) for persistence lengths between 1 nm and 100 nm. Contours for three step lengths are shown, ΔL = 0.3 nm (triangles), ΔL = 0.9 nm (squares), and ΔL = 1.5 nm (circles). Solid lines indicate step detection thresholds calculated from the exact formula, Eq. 10, and dashed lines indicate the SNR threshold calculated from the approximate formula, Eq. 25. L = 1000 nm, d = 1000 nm, in (A) L_p = 50 nm, and in (B) k_cat = 100 s⁻¹. In panel B, the dotted line indicates the border between the high-force (III) and the medium-force (II) regions.

FIGURE 8.

SNR is inversely proportional to the square-root of the bead radius, and inversely proportional to the WLC contour length. Simulated step detection threshold contours (SNR = 4) as a function of F_C for (A) microsphere diameters between 0.1 and 10 μm, and (B) for WLC contour lengths between 100 nm and 10 μm. Contours for three step lengths are shown: ΔL = 0.3 nm (triangles), ΔL = 0.9 nm (squares), and ΔL = 1.5 nm (circles). Solid lines indicate step detection thresholds calculated from the exact formula, Eq. 10, and dashed lines indicate the SNR threshold calculated from the approximate formula, Eq. 25. L_p = 50 nm, k_cat = 100 s⁻¹, in (A) L = 1000 nm, and in (B) d = 1000 nm.

DISCUSSION

Designing experiments for measuring step length of molecular motors requires quantitative assessment of the experimental parameters which can be adjusted to achieve sufficient SNR. Measuring molecular motor step length from bead position time-series is complicated by the effect of the compliant tether and by thermal fluctuations of the bead. The finite tether stiffness affects the magnitude of thermal noise (Eq. 7), and causes step attenuation (Eq. 9 and Fig. 6 B), i.e., the apparent shortening of the measured steps compared to the true step size. To observe steps, thermal fluctuations larger than the attenuated step size must be averaged out, limiting the bandwidth of the measurement.

Here we present an approximate model that quantitatively and explicitly accounts for the motor properties, tether elasticity, and bead fluctuations, and can be used to optimize experiments. We first discuss the validation of the model by simulations. Then we expose the impact of each model parameter on SNR and discuss optimizing tethered-bead constant-force assays. Finally, we compare the theoretical predictions with published experimental results for selected NA motors.

Validation of the approximate model

The approximate theoretical model accounts for the salient features of the experimental system. This is demonstrated by the good agreement between the theoretical and simulated results in Figs. 6–8. The discrepancies between simulation (symbols) and theory (solid lines) are due to the theory only describing an equilibrium state of the system. The simulation takes into account the drag force on the bead which results in a settling-time before equilibrium is reached. Thus, in simulations we expect that a higher force is required to reach the threshold SNR in cases with fast motors (Fig. 7 A) or big beads (Fig. 8 A). A general tendency for the SNR threshold obtained from simulation to lie at higher force than the theoretical threshold can be explained by the finite roll-off of the bandwidth-limiting low-pass filter employed in the analysis of the time-series. The filter allows slightly more thermal noise to pass than an ideal filter assumed in the theory. The closed form high-force SNR approximation (Eq. 25, dashed lines) agrees well with the exact SNR (Eq. 10, solid lines).

Optimization of experimental parameters for step size detection

Below we discuss the effect of different experimental parameters on the SNR in the high-force regime in which steps are most likely to be detected. External force has the strongest impact on SNR (SNR is proportional to F^1.58), so clamp-force should ideally be maximized for step length measurements. However, the stalling force of the molecular motor limits the usable clamp-force. Measured stalling forces range from a few pN (38) up to and exceeding 50 pN for viral packaging motors (39). A high clamp-force results in increased WLC extension and a stiffening of the system due to the nonlinear force-extension relationship. This stiffening reduces thermal fluctuations. However, fluctuations on the order of the step length are essential for molecular motors using the Brownian ratchet mechanism (40). For these motors the stalling force should therefore be close to the force necessary for single step observation. This was recently confirmed experimentally for an RNA polymerase (8). In addition, the structural strength of the tether and associated handles (e.g., complementary DNA oligos attached to ssDNA tether) limits the maximum usable clamp-force.

SNR is inversely proportional to the WLC contour length. Tether length is mainly limited by experimental design, i.e., interference from surface-effects between the bead and microscope coverslip or interaction between the two beads in the dual-trap (dumbbell) setup. Tether length should be minimized whenever possible; in practice, tethers of similar length to the bead diameter have been used.

The persistence length of the tether is crucial in determining the overall stiffness, and consequently the magnitude of thermal noise of the system. SNR is proportional to 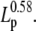A long persistence length, or buffer conditions that maximize L_p, should be chosen whenever possible. At very low extensions, a shorter persistence length may increase the local WLC stiffness (κ), but these conditions also yield very low SNR (Eq. 10). In particular, our results suggest that the use of double-stranded substrates, compared to single-stranded substrates, improves the possibility of detecting short steps. This could be experimentally verified for helicases that translocate along ssNA substrates but are able to unwind dsNA. A motor running exclusively on ssNA can be studied using a short ssNA substrate with longer stiff dsNA handles at each end.

Although the step rate and the bead diameter affect SNR most weakly (SNR is proportional to 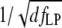) these experimental parameters can be readily varied. Slowing down the molecular motor, and thus reducing the measurement bandwidth, offers a simple way of increasing SNR in an experiment. This can be done either by changing the temperature of the sample solution (41), by using clamp-force as an inhibitor (42), or by restricting the step rate by lowering ATP concentration (when ATP binding constitutes the rate limiting step). Measurements at these nonphysiological conditions still provide relevant information about the function of a molecular motor in vivo since the lengths of the elementary steps are determined by the molecular architecture of the motor rather than by external conditions.

Single molecule measurements on the nanoscale require micron-sized beads as handles to couple the experiment to macroscopic instrumentation. A macroscopic handle effectively transmits the thermal bath fluctuations to the microscopic system and thus constitutes a significant noise source. Decreasing the bead size reduces the power of the noise source. The minimum bead size is limited by the requirement to resolve individual beads by light microscopy and, for optical-tweezers-based measurements, by the dependence of the trapping force on the bead volume. The smallest bead for which the desired clamp-force can be achieved should be chosen. However, small beads require high trapping laser power, so the increase in SNR must be weighed against unwanted damage and local heating of the specimen (43,44).

In this study we have assumed ideal instrumentation, i.e. absence of 1/f (pink) noise in the bead position detection. Close approximations to this situation have recently been realized using either an optically levitated dumbbell assay (8), or differential detection (26,45), which decouple or compensate for stage-drift (the dominating noise source at low frequencies). In practice, a balance between the benefits of limiting the observation bandwidth, which allows longer averaging of the zero-mean thermal noise, and shortening the measurement time, which limits instrumentation related 1/f drift, has to be found. Optimization of the measurement time, by including 1/f noise in the model, could easily be done by adding a 1/f noise source to the simulation, but we have not found a straightforward way to include 1/f noise in the theoretical formulas presented here.

Comparison with experimental data

Since instrumentation with sub-nanometer noise levels has only become available recently, the step length for NA bound molecular motors has been successfully determined only for one RNA polymerase. In this section we apply the theory to compute a theoretical SNR and compare it to experimental SNRs from several single molecule studies on polymerases and helicases translocating on dsDNA substrates. We limit ourselves to the studies in which the conditions used were described at the necessary level of detail. These comparisons show that the theoretical predictions correlate well with the success or failure to observe discrete steps. The comparisons are summarized in Table 2.

TABLE 2.

SNR for recent NA translocating single-molecule motor experiments

Motor	Bead diameter (nm)	Clamp force (pN)	Step rate (s−1)	Step length (nm)	Contour length (nm)	SNR (Eq. 10)
RNA Polymerase, Wang et al. (7)	500	10	25	0.34	1500	∼2.4
RNA Polymerase, Shaevitz et al. (2)	500	8.4	15	0.34	2000	∼1.8
RNA Polymerase, Thomen et al. (42)	500	15.5	15	0.34	16000	∼0.5
RNA Polymerase, Abbondanzieri et al. (8)	600	18	0.5	0.37	2000	∼28
φ29 portal motor, Smith et al. (39)	2200	57	100	0.68	6600	∼1.7
RecBCD, Perkins et al. (28)	460	7	2	0.34	852	∼9

Double-stranded DNA with a persistence length of 50 nm, and room temperature (T = 300 K) was assumed for all experiments. Where a range of values were used in the experiments, the values maximizing SNR have been chosen, and the SNR calculated using Eq. 10. Abbondanzieri et al. (8) were the only ones to observe steps of RNAP at SNR ∼ 28. In the absence of instrumental noise, our analysis shows that Perkins et al. (28) could have observed single RecBCD steps at SNR ∼ 9.

Recently, Abbondanzieri et al. (8) observed single 0.37 nm steps of Escherichia coli RNA polymerase with a rate of k_cat ≈ 0.5 s⁻¹ using an assay with a 600-nm-diameter bead held in a 18 pN force-clamp. This corresponds to SNR ∼ 28, approximately fivefold higher than the detection threshold of SNR > 4 established by the proposed theory. We attribute this discrepancy to the fact that the theory does not account for instrumentation-related drift, and to the fact that the authors chose to present data where steps can be resolved by eye from the filtered time-series. Perkins et al. (28) did not observe discrete steps of RecBCD at SNR ∼9, most likely due to instrumental drift. We predict that a realistic experimental SNR threshold for detecting steps lies somewhere between the ideal-instrument lower limit of ∼4 derived here, and the value of ∼28 experimentally verified by Abbondanzieri et al. Notably, Wang et al. (7), Shaevitz et al. (2), Thomen et al. (42), and Smith et al. (39) all conducted experiments at SNR roughly close to one, and consistent with our prediction, did not observe discrete steps.

Although ssRNA binding to the ribosome was studied using OT (11) there has been no account of translocation along ssNA by any motor against applied force, let alone an attempt to determine the step. An assessment of the force required to detect steps of 0.5–1.5 nm (expected for many helicases) for a motor translocating on ssNA (L_p = 1 nm) (Fig. 7 B) leads us to conclude that this might be impossible, except for very slow or strong motors.

CONCLUSIONS

Using a simplified theory of a tethered bead, constant-force, single-molecule experiment, we have investigated experimental parameters that influence the detection of stepwise tether shortening. The simplified theory was verified by Monte Carlo simulation and is consistent with experimental results obtained for dsDNA. The theory allows assessment and optimization of experimental conditions for motors translocating along single-stranded NA substrates for which there is little experimental data available. Most importantly, in the absence of instrumentation-related noise, an SNR threshold of ∼4 was found for measuring step length, and in contrast to previous work where the tether stiffness was assumed constant (24,25), we have derived quantitatively the dependence of the SNR on the clamp-force and tether persistence length.