A Programmable Optical Angle Clamp for Rotary Molecular Motors

Abstract

Optical tweezers are widely used for experimental investigation of linear molecular motors. The rates and force dependence of steps in the mechanochemical cycle of linear motors have been probed giving detailed insight into motor mechanisms. With similar goals in mind for rotary molecular motors we present here an optical trapping system designed as an angle clamp to study the bacterial flagellar motor and F₁-ATPase. The trap position was controlled by a digital signal processing board and a host computer via acousto-optic deflectors, the motor position via a three-dimensional piezoelectric stage and the motor angle using a pair of polystyrene beads as a handle for the optical trap. Bead-pair angles were detected using back focal plane interferometry with a resolution of up to 1°, and controlled using a feedback algorithm with a precision of up to 2° and a bandwidth of up to 1.6 kHz. Details of the optical trap, algorithm, and alignment procedures are given. Preliminary data showing angular control of F₁-ATPase and angular and speed control of the bacterial flagellar motor are presented.

INTRODUCTION

Since their invention just over 20 years ago optical traps (1–4) have been widely used for research purposes in both physics and biology, ranging from the cooling and trapping of neutral atoms (5) to manipulating live cells and viruses (6,7). More recently, optical traps have been extensively employed in the experimental investigations of molecular motors (8,9). Their ability to apply piconewton forces to micron-sized particles, while simultaneously measuring displacement with nanometer precision, often makes them the best tool in practice. With the help of optical traps, the stepping behavior of the linear motors myosin (10), kinesin (11), and dynein (12) has been resolved. The implementation of “force clamps” and “position clamps” combining optical traps with controllable feedback systems provides more information about the motors' mechanochemical cycles and working mechanisms (13,14). With similar goals in mind for rotary molecular motors, the bacterial flagellar motor, and F₁F_O-ATPase, we have designed an optical trap to act as an “angle clamp”. We use a polystyrene bead duplex (bead pair) as a handle to apply external torque to rotary molecular motors. This technique allows us to achieve high temporal and angular resolution as well as great flexibility of control.

The bacterial flagellar motor (bfm) is a rotary motor ∼50 nm in diameter, embedded in the cell envelope and connected to an extracellular helical propeller (15,16). The motor is powered by the flow of ions down an electrochemical gradient across the cytoplasmic membrane into the cell (the protonmotive force, pmf, or sodium-motive force, smf). It has recently been shown to rotate with 26 steps per revolution, with each step corresponding to a linear step of ∼24 nm on the order of several milliseconds (17,18). F₁F_O-ATPase is an enzyme that utilizes the pmf or smf to synthesize ATP from ADP and P_i (19,20). It is a complex of two motors, F_O and F₁, with an overall size of ∼20 nm (21). Under normal conditions, the ion-driven, membrane-bound F_O forces the ATP-driven, cytoplasmic F₁ in reverse, leading to ATP synthesis in F₁. When separated from F_O, F₁ can hydrolyze ATP, leading to directly observable rotation of the γ-subunit relative to the α₃β₃ hexamer (22). Analysis of stepwise rotation consisting of 120° steps with 40° and 80° substeps (23,24) has led to a detailed understanding of the mechanism of the F₁ motor. With a 40-nm bead attached to F₁, the 120° step corresponds to a linear step between 40 and 120 nm, and a 40° substep to between 13 and 40 nm. The larger 80° substep in F₁ rotation depends on ATP binding, and has a rate on the order of seconds for [ATP] in the nanomolar range. The smaller substep, however, is [ATP] independent and is on the order of milliseconds or less (23,25,26). Thus the temporal and spatial resolutions required to detect features of interest in the rotation of these motors are on the order of milliseconds and tens of nanometers, respectively. The stall torques of 40–60 pN nm and up to 1000–2000 pN nm, generated by F₁ (23,25) and the bfm (18,27), respectively, set the scale of torque required to control these motors.

Due to its large stall torque, the preferred method for applying external torque to the bfm to date has been electrorotation, with cells tethered to the surface by a flagellar filament and the cell body acting as the handle on the motor (28). External torque has been applied to F₁ by using magnetic tweezers to control the angle of magnetic beads, 470–700 nm in diameter, attached to the γ-subunit. This technique has allowed the synthesis of ATP to be quantified (29,30), and the properties of the ADP-inhibited state to be investigated (31). These methods have drawbacks, however. The cell body is a large handle, and therefore requires extremely large torques to attain the high speeds (∼300 Hz) that are characteristic of the flagellar motor. Furthermore, the size of these handles and the way in which torque is applied do not lend themselves to the high spatial and temporal resolutions that are possible with optical traps. For example, the typical resolutions reported using magnetic beads are several seconds and 5° (31).

There is one report of the use of optical tweezers to exert torque on a rotary motor, to measure the stall torque of the bfm (32), and two similar reports of the use of tweezers to study the properties of the bfm hook and filament (33,34). In these experiments torque was applied to the motor in the form of linear force on the trapped particle. This situation is analogous to tightening a nut with a wrench. The trap is akin to hand holding the wrench, the cell body is the wrench, and the opposing reactive force that completes the couple is generated by the link between the motor and the surface. There are several reports of methods that apply torque directly to microscopic objects with optical tweezers. Because laser beams can carry spin and orbital angular momentum, torque can be exerted on a microscopic object if angular momentum is exchanged between the beam and the particle upon scattering. This has been achieved by exchange of the following: spin angular momentum with birefringent particles (35–40); spin angular momentum with asymmetrically shaped particles (41–43); orbital and spin angular momentum simultaneously with absorbing particles (44,45). Rotation within optical tweezers (by rotating an asymmetric interference pattern or a high-order laser mode, by the use of an elliptical beam, or by rotating an aperture (46–49)) and microfabricated chiral scattering particles that act as optical “windmills” have also been reported (50). These methods have several drawbacks, however. The need for special microparticles, like birefringent or “windmill” particles, limits the practicality of the method and potentially raises problems with attaching particles to rotary molecular motors. Techniques using energy absorption are limited due to heating, and methods that rely on rotation within optical tweezers require more complicated trapping systems to generate specialized beams. Shaped particles and beams carrying orbital angular momentum have typical dimensions of several microns, and thus the viscous drag on trapped particles limits the response time of these particles to changes in torque. Modulation of shaped beams generated by micromirror or liquid-crystal technologies also limits the time resolution of these techniques.

Our system uses a digital signal processing board for control of the optical trap and allows us to achieve control of the rotation angle of bead pairs with a bandwidth up to 1.6 kHz and angular precision of 2°, while at the same time affording great flexibility when choosing and designing feedback algorithms for rotary molecular motors. We describe and characterize alignment and calibration of our technique and implementation of nonlinear feedback algorithms. We demonstrate the capability of our method to observe fluctuations in the bfm most likely caused by incorporation and removal of individual torque-generating units, to control the speed of the bfm, and to control the angle of the rotating γ-subunit of F₁. We discuss complications related to calibration and mechanical damage to motors using our method, and conclude that it will be a useful tool in future experiments to investigate in detail the mechanism of rotary molecular motors.

METHODS

Instrument design

The instrument consists of a custom-built inverted microscope and two lasers for detection and trapping (51). Bright-field imaging uses a high-power light-emitting diode (Luxeon Star LEDs, Alberta, Canada), high N.A. condenser (MEL 30920, Nikon, Tokyo, Japan) and objective (Plan Fluor 100× / 0.5–1.3 oil iris, Nikon), and a high-sensitivity ½-inch black and white charge-coupled device video camera (LCL-902K, Watec, Orangeburg, NY). The microscope stage was designed to be light and compact to minimize drift and vibration. Microscope slides holding specimens are attached to a metal plate mounted on a three-axis piezoelectric stage (P-611.3S nanocube with E-664 LVPZT amplifier/servo-driver, 100 μm travel in x, y, z, 1 nm resolution, with a settling time of a few milliseconds, Physik Instrumente, Karlsruhe, Germany), which is in turn mounted on a lockable three-axis dovetail stage (Newport, Didcot, UK) for coarse positioning.

Position detection is by back-focal-plane interferometry (52) using a laser beam (helium-neon, 632 nm, 17 mW, Coherent, Santa Clara, CA) focused into the specimen plane by the objective and collimated onto the face of a quadrant photodiode (QD) (UDT Sensors, Hawthorne, CA). After amplification the QD signals are passed through antialiasing first-order prefilters with time constants ranging from 0.625 ms to 6.25 μs and digitized at an appropriate sample rate (53). Detector range can be increased from 400 to 1200 nm at the expense of sensitivity by reduction of the laser beam width (using a detector beam iris). The intensity of the detector laser is controlled by the iris aperture and neutral density filters, according to the requirements of particular experiments.

The optical trap is formed by a near-infrared Ytterbium fiber laser (PYL-3-LP, 1064 nm, 3 W continuous wave, IPG Photonics, Pittsfield, MA), collimated by the manufacturer, with <3% power fluctuation in 4 h. We measured pointing fluctuations of this laser of ∼2.5 μrad (rms) in 1 h, with the spectral characteristics of white noise above ∼30 Hz and 1/f noise below ∼30 Hz. The intensity of the trapping laser was varied via the diode current and the combination of a half-wave plate and polarizing beam splitter. Fine control of the trapping laser is achieved with acousto-optic deflectors (AOD) AA.DTS.XY.250 at 1064 nm, AA.DDS.60-90.XY driver, Opto-Electronique, Orsay, Cedex, France), positioned in a plane conjugate to the back focal plane of the objective. The angular range and resolution of the AOD are 49 mrad and 24.9 μrad, respectively. The smallest movement of the trapping laser is 9 nm, and the AOD response time is 0.1 ms.

Data acquisition, feedback calculations, and control of the optical trap were all performed by a digital signal processing board ((DSP) SI-C33DSP-PCI, 150 MHz processor speed with SI-DSP6433R2-PCI daughter module, 16 analog input channels, four analog output channels with sampling rates up to 50 kHz, Sheldon Instruments, San Diego, CA) installed in a host computer (1.8 GHz processor, 1 GB RAM) running Windows 2000. The board was programmed using a software package, QuVIEW, provided by the manufacturer. Feedback programs on the DSP board were run at 10 kHz sampling rate unless otherwise stated. Analog output channels from the DSP daughter module were converted to digital for the AOD control by a custom-made analog to digital converter that gave a scan range and resolution of 27.5 MHz and 15.3 kHz, respectively, corresponding to 44.9 mrad and 24.9 μrad beam deflection and 16.5 μm and 9 nm displacement of the optical trap. For typical rotational trajectories of 100–1000 nm beads attached to motors, 9 nm corresponds to an angular resolution of 1–10°, depending on the radius of the circle along which the trapping laser is moved.

The trapping laser was chosen for low cost, high power, and the relatively low levels of laser-induced photodamage to biological samples at this wavelength (54). The helium-neon laser used for detection, with its shorter wavelength, allows a smaller focused spot and therefore improved detector sensitivity, especially for beads with diameters below ∼500 nm. It also has excellent beam quality and avoids potential difficulties with effective low-pass filtering (8–9 kHz) that can occur with silicon photodiodes and 1064-nm lasers (55,56). We characterized the photodamage caused by the detector laser by recording laser-induced changes in the speed of a bead attached to a rotating flagellar filament of Escherichia coli (18) over the range of laser powers used (20–150 μW in the objective back-focal-plane). Using a speed reduction of 5% to define a threshold for laser damage, we were able to record for 1.5–2 min at 150 μW and for 5–10 min at 20 μW before observing any laser damage. By contrast, previous work has shown that similar speed recordings using a laser at 1064 nm can be extended for hours without observable laser damage (27). Protein motors such as F₁ are typically less sensitive to photodamage than live cells, and can be protected by the addition of singlet-oxygen scavengers (22) if necessary.

Alignment and calibration of the detector and AOD

The dimensionless signal (X,Y) obtained from the detector by bfp interferometry of a single bead was calibrated and the effect of the bead height (focus, z) on the (X,Y) signal measured as described previously (51,52). At the beginning of each experiment z = 0 was defined such that the average brightness of the bright-field image of the bead was similar to the background; thus, beads appeared gray at z = 0, black at z > 0 (by definition, when the microscope and laser focus was in the sample buffer), and white at z < 0 (focus in the coverglass), as illustrated in Fig. 2 c. By setting z = 0 by eye 20 times each for nine different beads and recording the spread of actual heights read from the calibrated piezoelectric stage, we estimated that this procedure sets z = 0 with an accuracy of ∼30 nm. This is comfortably within the range of ∼400 nm over which the variation of X or Y with z is negligible (data not shown), therefore we neglected any possible effects of z drift on the detector response (X,Y).

FIGURE 2.

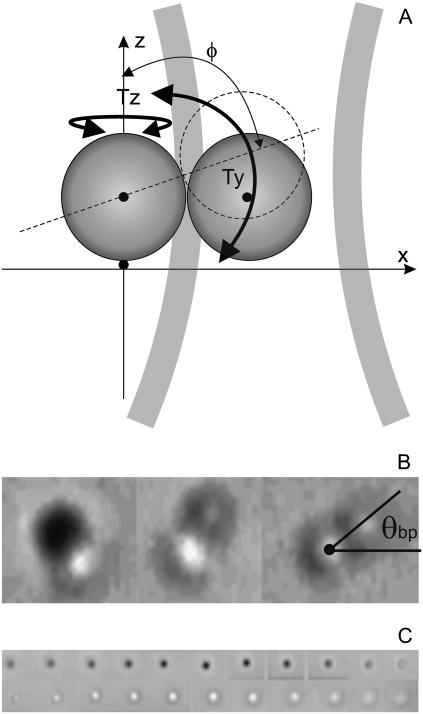
(A) Schematic diagram of a bead pair attached to a surface by a motor at x = y = z = 0 and held by the optical trap. (B) Bright-field video microscope images of bead pairs with different values of the angle φ as defined in panel A. We chose pairs with φ ∼ 90° like the one in the right panel, for which the angle θ_bp is defined. (C) Bright-field images of a single bead scanned in 100-nm steps in z. The accuracy with which z = 0 could be set by eye using video images was found to be ∼30 nm.

We aligned the QD and AOD in the following way. 1), We moved a bead stuck to the coverslip surface through the detector laser focus with the piezo stage and defined the center of the detector beam as the midpoint of the single-valued range of the X and Y signals. 2), With the bead at this center, we set X and Y to zero by adjustment of a mirror that steers the detector laser beam onto the QD. 3), We repeated steps 1 and 2 several times to remove any sensitivity to the initial state of alignment. 4), With the AOD set at the center driving frequency and the stuck bead replaced by a bead trapped a few microns from the coverslip, we again set X and Y to zero. The bead position, (x, y), was calculated in real time on the DSP board from the signal (X,Y) using a fifth-order polynomial fit (51,52), with fit parameters obtained by scanning the same bead (or another bead of the same size in the same sample) with the AOD immediately before each experiment.

Trap stiffness

We calibrated the trap stiffness for single beads using either Brownian motion of the bead and the Principle of Equipartition of Energy (52), or by fitting the power spectrum of the Brownian motion to a model that accounts for discrete sampling of the data, low-pass filtering by the QD, and inertial effects from the entrained fluid surrounding the bead (52,53,57). One unavoidable property of AOD is that the intensity of the deflected beam varies with the angle of deflection. We were able to limit this intensity variation over the full range of the AOD to <8% by choosing the appropriate driving amplitude for the range of frequencies used. The remaining variation was characterized by measuring the trap stiffness at different positions, and was found to follow the intensity variation as expected.

Feedback algorithms

To control the position of a single trapped bead in two dimensions we used the standard proportional-integral feedback algorithm (58). To control the angle coordinate of a bead or a bead pair, θ_b, we used:

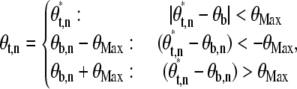(1)

where

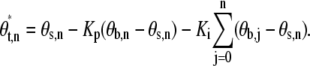θ_x,y are angle coordinates of the trap, bead (or bead pair), and set point (x = t, b, s, respectively) for a sample point indicated by the index y, and K_p and K_i are proportional and integral feedback parameters. θ_Max is a constant. The radial coordinate of the trap position remains constant. This nonlinear algorithm ensures that the angle between the trap and the bead (proportional to torque) never exceeds θ_Max (in our experiments typically 90°) and thus that the torque on the bead will be in the correct direction even for large error signals and gain.

Feedback bandwidth, f_FB, is limited by the trap stiffness at low laser power and at higher laser power by the delays due to the finite AOD response time and the computational time on the DSP board. f_FB increased with K_p and K_i up to a maximum of 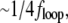where f_loop is the overall feedback execution frequency, after which the oscillations at 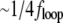were observed. This is in agreement with predictions from a simple calculation for an analog first-order system using the methods of Bechhoefer (58), with the effect of delays taken into account.

Bead-pair preparation

We used amino-functionalized, biotinylated, and plain polystyrene microspheres (diameter 500 nm, Polysciences, Eppelheim, Germany). Biotinylated microspheres (beads) were prepared by incubation of amino-functionalized beads, 1% by volume, for 2 h at room temperature with rolling, in 100 mM sodium bicarbonate buffer pH = 8.05 plus 2 mM 6-(biotinamidocaproylamido)caproic acidin-hydroxysuccinimideester (Sigma-Aldrich, Gillingham, UK) added as 100 mM stock in dimethyl sulfoxide (Sigma-Aldrich), followed by resuspension in storage buffer (10 mM HEPES/NaOH, pH = 7.8). Bead pairs were prepared by incubating beads in media with high salt concentrations, which is assumed to collapse the Debye layer and to allow beads to stick to each other by van der Waals interactions. We used 100–340 mM KCl for plain polystyrene beads and 100 mM MgCl₂ for biotinylated amino beads, both in storage buffer. Bead concentrations were between 0.5% and 2% by volume. After adding salt, beads were sonicated for 4–10 min and washed three times in storage buffer to a final concentration of ∼0.5%. Immediately after washing 10–15% of all objects in the solution were bead pairs. The bead pairs were separated from single beads and clumps containing more than two beads by sucrose gradient centrifugation and washed three times in storage buffer. Immediately after gradient separation 60–80% of all objects in the solution were bead pairs.

Bead-pair assay

Biotinylated bead pairs were attached to the surface of a coverslip as follows. The coverslip was cleaned with saturated KOH in 95% ethanol before use. A tunnel slide was constructed using double-sided adhesive tape to define a channel between the coverslip and a microscope slide, filled with Buffer A (10 mM MOPS/KOH, 2 mM MgCl₂, 50 mM KCl, pH 7) containing 6 mg/ml bovine serum albumin (Sigma-Aldrich) and incubated for 1 min. 4 μM streptavidin (Sigma-Aldrich) in Buffer A was then added and incubated for 10 min. After washing with Buffer A, 0.5% biotinylated bead pairs in Buffer A were added and incubated for 10 min.

F₁ rotation assay

E. coli F₁ with six histidine residues introduced into the α-subunit and two cystine mutations in γ-subunit was purified as described (59,60). Microscope coverslips were cleaned and assembled into tunnel slides as described above (BSA surface), or cleaned as described above and then a), coated with nitrocellulose (collodion solution, Sigma-Aldrich) and 1 μM Ni-NTA HRP (Qiagen, Crawley, UK) (HRP surface); or b), functionalized by a silane coupling agent before reaction with 10–15 mg/ml maleimide-C₃-NTA (Dojindo, Kumamoto, Japan) and then 10 mM NiCl₂, essentially as described (29,61) (silane surface). The coverslips were then assembled into tunnel slides as described above. The following were flowed through the channel: 1 nM F₁ in Buffer A+BSA, wait 10 min; Buffer A+BSA; 4 μM streptavidin (Sigma-Aldrich) in Buffer A, wait 10 min; Buffer A+BSA; 0.5% biotinylated bead pairs in Buffer A+BSA, wait 10 min; Buffer A+BSA; 24 mM Mg-ATP in Buffer A+BSA.

E. coli rotation assay

Cells of E. coli strain KAF95 (expressing flagellar filaments that spontaneously stick to plain polystyrene beads and flagellar motors that do not switch direction (28)) were grown, prepared, and labeled with plain polystyrene beads or bead pairs attached to truncated flagellar filaments as described (18).

TWO-DIMENSIONAL FEEDBACK CONTROL OF A SINGLE BEAD

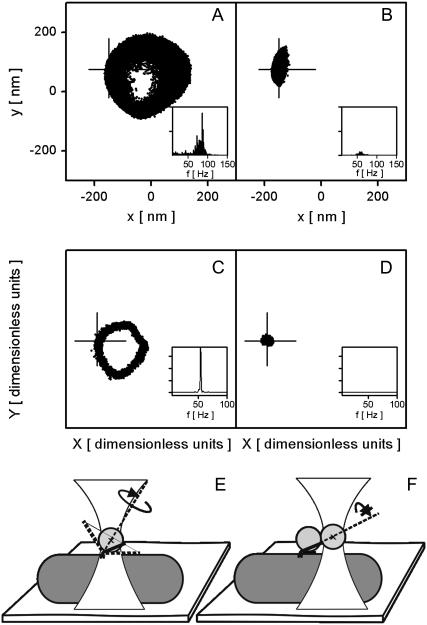
If a single bead is rigidly attached to the rotor of a molecular motor, then the only degree of freedom is the bead-rotor link angle and thus controlling the position of the center of the bead controls the motor angle as desired. However, beads are usually attached to the bfm via the sticky flagellar filament and the hook, which acts as a flexible universal joint. Fig. 1 A shows the x- and y-position signals obtained from a 500-nm bead attached to a flagellar filament, with no optical trap. The speed of the bead obtained from the power spectrum (inset, (18)) is ∼60 Hz. Fig. 1 B shows the same signals with the bead held at a point on the original orbit by independent feedback in the x and y axes. The motion of the bead was severely constrained compared to the original circular orbit, but the peak in the power spectrum indicates that the motor and bead are still rotating. This is possible because the hook can flex in such a way as to allow the filament stub to describe a cone, tangent to the bead with its apex at the motor, as illustrated in Fig. 1 E. Because the hook is a universal joint, this allows the motor to rotate about its (vertical) axis while the bead rotates about an axis joining the motor to the bead center. Because the latter axis passes through the center of the bead, the bead can rotate even if its center is prevented from moving by the optical trap. By contrast, Fig. 1 C shows the QD signal from a rotating bead pair and Fig. 1 D illustrates that there was no rotation of the motor when we held the pair stationary with the optical trap at a fixed point. Unlike with a single bead, there is no possible rotation axis passing through the motor and the bead pair, which is also a symmetry axis of the pair, and thus any rotation of the motor will be coupled to detectable rotation of the pair. In particular, rotation about the axis joining the motor and the center of the trapped, outer bead is blocked by interaction between the inner bead and the cell surface as indicated by the black bars in Fig. 1 F.

FIGURE 1.

Stalling the bacterial flagellar motor with an optical trap. (A) (x, y) position of a single 500-nm bead attached to a freely rotating bacterial flagellar motor and (B) held by the trapping laser in conventional proportional-integral feedback at a point along the rotation trajectory of panel A indicated by the cross. Laser power was 25 mW and feedback parameters K_p = 0.4 and K_i = 0.02. (C) QD signal (X, Y) of a rotating 500-nm bead pair attached to the bacterial flagellar motor and (D) held with the trapping laser at a fixed point indicated with a cross (along the trajectory of free bead-pair rotation in panel C). Laser power, 50 mW. (Insets) Power spectra of QD signal X, indicating the speed of bead rotation. Note that the motor is still spinning in B but not in D. (E) Schematic representation of a single bead experiment on the bacterial flagellar motor. A cell is fixed on a coverslip surface and a 500-nm bead attached to the bacterial flagellar motor via a filament stub. The center of the bead is indicated with a cross and the bead rotation axis is indicated with a dashed line and curved arrow. The bead can rotate even when held fixed, due to the universal joint properties of the hook. This enables the motor to rotate as well. (F) Schematic representation of a bead-pair experiment on bacterial flagellar motor. Black bars indicate that the rotation of the bead pair around its axis is blocked by the interaction between the inner bead and the cell surface, whereas the outer bead of the pair is held by the trap. This allows the motor to be stalled by holding the bead pair fixed with the trapping laser.

FEEDBACK WITH BEAD PAIRS

A bead pair is necessary to control the rotation angle of the bfm with an optical trap. It also has advantages for use with F₁. The asymmetry of a pair allows rotation to be observed directly, rather than relying on displacement of the center of a single bead due to eccentricity of rotation. Also, the bead pair acts as a lever arm, allowing more torque to be applied to the motor. However, the use of a bead pair as the handle of choice results in several specific problems, which we address here.

Alignment

When replacing a single bead with a bead pair, the calibration of the QD for a single bead no longer applies. Instead we note that for experiments with rotary motors we are interested only in the angle of the projection of the long axis of the bead pair onto the plane perpendicular to the motor's rotation axis. If the motor's axis is aligned with the microscope axis, this is the same as the angle of an image of the bead pair, which we designate θ_bp (Fig. 2 B). To estimate θ_bp from the QD signal (X,Y), we performed a rectangular-to-polar conversion (X,Y) → (R_bp, Θ_bp) and assumed that Θ_bp = θ_bp. To ensure that this estimate of θ_bp is reasonable it was necessary to close the detector laser iris, extending the monotonic range of the QD to cover the size of a bead pair. We demonstrated feedback control of the angle of pairs of biotinylated beads each 500 nm in diameter, attached to a microscope coverslip via streptavidin and BSA (Methods). We selected pairs that showed free rotational Brownian motion ((RBM) indicated by completion of at least one revolution within 10–20 s), indicating a single point of attachment on one of the beads. Conversion of QD signals and optical trap positions into angles is very sensitive to alignment of the centers of the QD and AOD range. We performed this alignment using single beads at the beginning of each experiment, as previously described. With bead pairs attached to the surface, a further alignment of the point of attachment with the QD and AOD centers is also required. We used two indicators to perform this alignment. Initial, coarse alignment we achieved by moving the stage so that the QD signal due to RBM (with no optical trap) became approximately circular. Subsequent, fine alignment was achieved by rotating the optical trap slowly in a circle centered on the AOD and the QD origin, and moving the stage to minimize variations in θ_bp − θ_t, which we took to indicate that the point of attachment was at the center of the AOD circle. The fine alignment procedure optimized the circularity of the QD signal, confirming that the attachment point, QD and AOD centers were all aligned. For pairs of 500-nm beads, we found that the fine alignment procedure could be successfully applied if the radius of the circle described by the trap was between 300 and 600 nm.

Feedback control of bead pairs

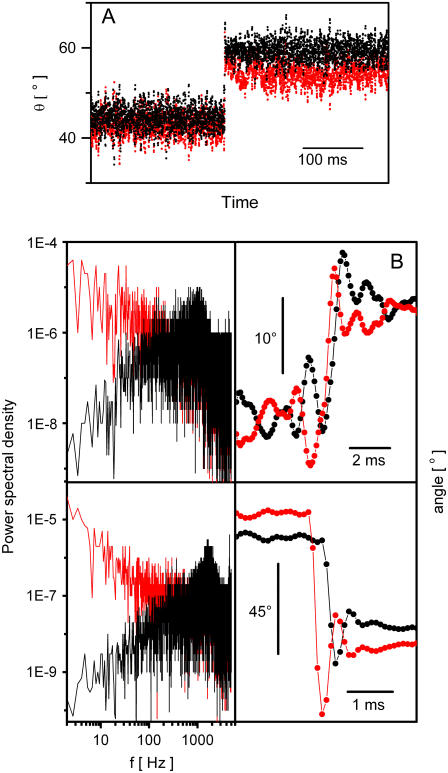
Fig. 3 shows results of applying the angular feedback algorithm of Eq. 1 to a bead pair, attached to the surface via biotin-streptavidin link, that showed RBM with a nearly circular QD signal. Fig. 3 A shows the angles of the trap θ_t (red) and bead pair θ_bp (black) versus time when the set-point angle θ_s was changed by 15°. The standard deviation of bead-pair angles at each set point was ∼2°. Fig. 3 B (top left) shows the power spectra of θ_t (red) and θ_bp (black) when a bead pair was held at a fixed angle with the same feedback parameters and laser power as in Fig. 3 A. Fig. 3 B (top right) shows the transient response to the change in set point on an expanded timescale, illustrating that the system response time was ∼2 ms. Fig. 3 B (bottom) shows the power spectra and transient response with the same feedback parameters and increased laser power. In this case the rise time was reduced to ∼1 ms. In both cases the feedback was very stiff, approaching critical behavior as indicated by the peak in the power spectra and damped oscillations in the step response. The frequency at which the instability occurs is in agreement with our expectations (∼1/4 f_loop). The small difference between θ_t and θ_bp when the set-point was not changing is evidence of imperfect alignment between the trapping laser and the bead pair, which we found very difficult to eliminate.

FIGURE 3.

Control of bead-pair angle. (A) The angular feedback algorithm of Eq. 1 was applied to bead pairs, attached to the surface via biotin-streptavidin link that showed free RBM. Angles of the trap (θ_t) and bead pair (θ_bp) are shown in red and black, respectively. The set-point angle θ_s was switched from 45° to 60°. Trapping laser power was 18 mW and radius 0.3 μm (resulting in a minimum angular movement of the trapping laser of ∼2°). Feedback parameters were K_p = 0.8 and K_i = 0.2. The mean bead-pair angles and standard deviations are (44.5 ± 2.4)°, (59.3 ± 2.2)° for θ_s = 45°, 60°. Bead-pair angle and trap angle were passed through a low-pass second order Chebyshev filter before display, with f_pass = 450 Hz. (B) (Top left) Power spectra of θ_t (red) and θ_bp (black) for a bead pair held at a fixed angle with the same feedback parameters and laser power as in panel A, and (bottom left) with laser power increased to 85 mW. (Top right) θ_t (red) and θ_bp (black) versus time showing the response to a change of a set-point, for 18 mW laser power. System response time is ∼2 ms; (bottom right) with 85 mW laser power the system response time is reduced to ∼1 ms.

Angular trap stiffness

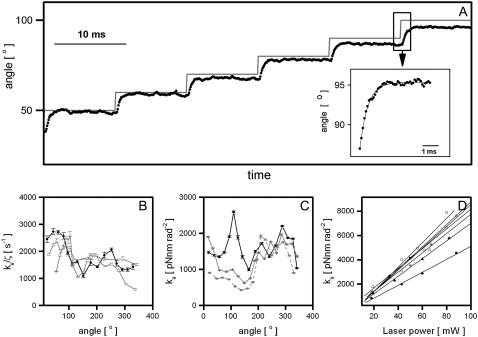
Fig. 4 A shows θ_t (gray) and θ_bp (black) versus time as the trap is moved on a circle in 10° steps without feedback. Bead pairs were attached to F₁ molecules (Methods), but we selected pairs that exhibited free RBM when not trapped. (Such nonrotating pairs were very common in F₁ rotation assays; we suspect that they represent either damaged F₁ molecules or freely rotating F₁ molecules where only one of the three His-tags is attached to the surface.) We also selected “flat” bead pairs, those with angles φ close to 90° (Fig. 2, A and B (right)), for reasons discussed below. The angles shown are averages over 40 successive rotations lasting a total of 15 s. We calculated the relaxation time of the system, ζ_θ/k_θ (where k_θ is the torsional stiffness of the trap and ζ_θ is the rotational viscous drag coefficient of the bead pair) from an exponential fit of the response to each step (Fig. 4 A, inset) at each angle. Analysis of the RBM between steps provides an estimate of k_θ. We use the equipartition method, 1/2k_θ 〈Δθ²〉 = 1/2k_BT, instead of the power spectrum method because the rotational viscous drag coefficient of a bead pair attached to the surface is not known.

FIGURE 4.

Calibration of the angular trap stiffness for 500-nm nonrotating bead pairs attached to F₁ molecules. (A) Bead-pair angle, θ_bp (black), and trap angle, θ_t (gray), versus time for a bead pair in a trap moving in 10° steps without feedback. Angles are averages over 40 successive rotations. (Inset) Step-response, with exponential fit. (B) The ratio of angular trap stiffness to rotational viscous drag coefficient, derived from the time constants in the fits in panel A as described in the text, versus angle, for three bead pairs on HRP surface (black) and silane surface (gray) (Methods). (C) Angular trap stiffness versus angle for the same bead pair as in panel B (black) and two additional bead pairs (gray) on silane surface. (D) Trap stiffness using at 45° versus laser power for several bead pairs on a BSA surface (Methods). Data were sampled at 10 kHz, laser power in panels A–D was 30 mW, and the trap was kept on 0.42 μm radius circle. Bead pairs with φ ∼ 90°, which performed free rotational Brownian motion without the trap were chosen for all calibration experiments. Error bars in B and C are standard errors obtained by averaging values of ratio of angular trap stiffness to rotational viscous drag coefficient and angular trap stiffness of two adjacent angles.

Fig. 4 B shows k_θ/ζ_θ vs. θ_bp for three F₁ bead pairs on HRP (black) and silane surfaces (gray). Fig. 4 C shows k_θ vs. θ_bp for the same F₁ bead pair on HRP surface as in Fig. 4 B (black), and two other bead pairs on a silane surface (gray). Fig. 4 D shows k_θ versus laser power, for several F₁ bead pairs held at 45° on a BSA surface. Trap stiffness is linear with laser power for all bead pairs, but the slope (dk_θ/dP, where P is laser power) varies from pair to pair. The different shapes of the curves for k_θ/ζ_θ and k_θ most probably reflect angular dependence of ζ_θ. This has been observed for the flagellar motor as a variation in the speed of an untrapped motor with angle (62) and may equally apply to F₁. Possible sources of angular variation and variation between bead pairs are discussed below. Many questions can be answered by comparing relative motor torque under different conditions. However, if accurate measurement of absolute torque is required it will be necessary to calibrate the angular trap stiffness for each bead pair after inactivating the motor at the end of each experiment. We have developed and presented here a calibration procedure that can be completed in a few seconds and implemented as part of the experimental protocol.

Preliminary experiments with rotary molecular motors

In this section we describe preliminary experiments in which we demonstrate the application of our system to single-molecule assays of rotary molecular motors.

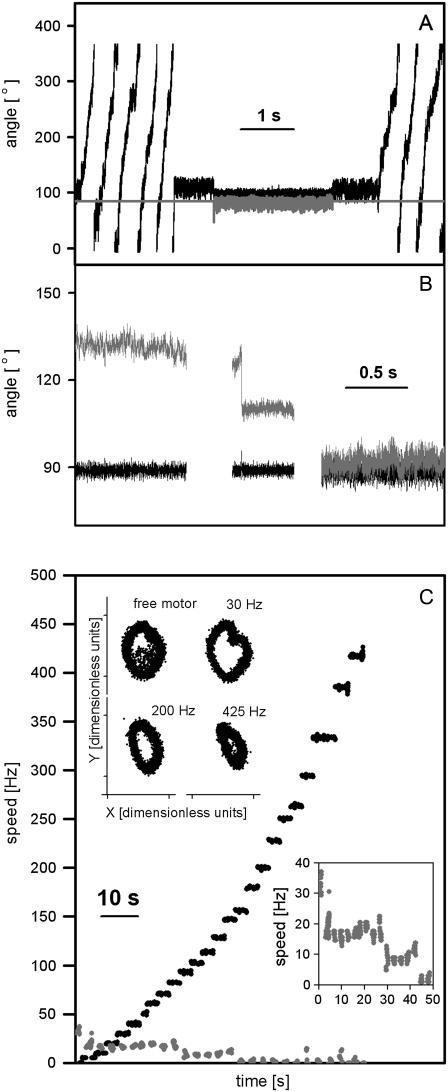
Fig. 5 A shows control of the angle of a 500-nm bead pair attached to the rotating γ-subunit of F₁ (Methods, (23)), using the feedback algorithm of Eq. 1. The angles of the bead pair, θ_bp, and trap, θ_t, are shown in black and gray, respectively. After ∼5 revolutions with the trap shuttered and the motor rotating freely, the shutter is opened and the motor stalled by a fixed trap at θ_t = 90°. Approximately 0.5 s later feedback is switched on for ∼2 s, with a set-point of θ_bp = 90°, and then switched off again, leaving the trap at θ_t = 90°. Finally, the trap is shuttered and the motor starts rotating as before. This was repeated eight times for the bead shown and for 12 different bead pairs attached to F₁ (data not shown). We did not calibrate this particular bead pair, so we cannot give an accurate estimate of the stall torque. If we estimate the trap stiffness from the signal of the stalled motor without feedback by using the Principle of Equipartition of Energy, we have k_θ = 438 ± 116 pN nm rad⁻² and a stall torque of T_stall = k_θ 〈 θ_bp −θ_t 〉 = 74 ± 20 pN nm. This is higher than the values of 40 pN nm and 63 pN nm estimated by other methods (23,25), perhaps because the stiffness of the intact F₁ adds to the trap stiffness leading to an overestimate of the latter. This preliminary experiment demonstrates that we can control the angle of F₁ with high accuracy and time resolution, and that the procedure does not appear to damage the motor.

FIGURE 5.

(A) Bead-pair angle, θ_bp (black), and trap angle, θ_t (gray), for a 500-nm bead pair attached to the rotating γ-subunit of F₁. The bead pair rotated at the beginning and end of the record when the trap was shuttered. The feedback algorithm of Eq. 1 was used to hold θ_bp = 90° in the middle of the record. At other times, the bead pair was held in the trap with no feedback. Feedback parameters K_p = 0.8 and K_i = 0.2, radius of the trapping laser = 480 nm, laser power = 31 mW. (B) θ_bp (black) and θ_t, (gray) for a 500-nm bead pair attached to the bfm with the feedback algorithm of Eq. 4 used to hold θ_bp = 90°. The difference between trap angle and bead-pair angle corresponds to the bacterial flagellar motor torque. We interpret the data as showing a motor initially with two stator units losing first one and later both units, such that the torque goes from 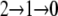times the torque of a single unit. Feedback parameters K_p = 0.8 and K_i = 0.1, radius of the trapping laser = 0.42 μm, laser power = 29 mW. (C) Control of the speed of the bfm using a 500-nm bead pair and the optical trap without feedback. θ_bp followed the trapping laser, which was rotated at different speeds up to 425 Hz (black). At regular intervals the trap was shuttered and the bead pair allowed to rotate freely (gray, expanded in lower inset). The stepwise reduction in freely rotating speed indicates a reduction in the number of torque-generating units in the order 3, 2, 1, 0. (Inset, upper) The QD X and Y signals for the rotating bead pair at different speeds. The trap radius was changed between 0.6 and 0.3 μm during the experiment and the laser power was 65 mW.

Fig. 5 B shows control of the angle of a 500-nm bead pair attached to the bfm using the same methods as described for Fig. 5 A. We applied feedback with different set angles during periods lasting 3 s or 10 s, alternated with periods of the same length when we allowed the motor to rotate freely, providing an independent measure of the motor torque and to determine whether any damage had occurred (data not shown). Fig. 5 B shows θ_bp (black) and θ_t (gray) for the periods when feedback was on and the set angle was 90°. Assuming that the trap torque is proportional to θ_t − θ_bp, we interpret the data of Fig. 5 B as changes in the motor torque from 2 to 1 times a unitary torque, and then to 0. The observed halving of the motor torque (Fig. 5 B, middle) most probably corresponds to a change from two torque generating units to one, similar to speed changes seen previously in freely rotating motors (18,27). We did not calibrate this particular bead pair, however, we subsequently subjected five other cells to the protocol of Fig. 5 B. A histogram of the freely rotating speeds recorded from those five cells showed peaks corresponding to different numbers of stator units ((27), Supplementary Fig. S1 B, see Supplementary Material). This allowed us to estimate the speed of a 500-nm bead pair driven by a single unit as 10.7 ± 3.3 Hz. Calibration of three of the five bead pairs used in these experiments allowed us to estimate the stall torque of the motors immediately before and after each free-running period (in total 35 torque measurements, Supplementary Fig. S1 A). We found that the stall torques were proportional to free running speed. Assuming that the torque changes very little between stall and the maximum free running speed of ∼100 Hz (28,63) we estimated the average viscous drag coefficient of the bead pair, ζ, to be 17 ± 2 pN nm Hz⁻¹, and the torque per stator unit to be 170 ± 40 pN nm in agreement with previous estimates (27).

Fig. 5 C shows the QD signal (inset, upper) and speeds of a bead pair attached to a bacterial flagellar motor, made to rotate at speeds up to 425 Hz by moving the trapping laser in a circle at a constant speed without feedback. As in the feedback experiment, above, we allowed the motors to rotate freely between periods of forced rotation to determine whether any damage had occurred. Speeds measured when the motor was under control of the trap are shown in black, and speeds of freely rotating motors are in gray. We stopped the experiment when rotation of the free motor was no longer observed.

DISCUSSION

In this article we present an optical trapping system designed for the study of rotary molecular motors. A host computer and DSP board are integral parts of the system allowing software control of feedback algorithms and time resolutions of milliseconds. We present several feedback algorithms. The two-dimensional X and Y feedback algorithm gives essentially the same control of the trapping laser as used for studies of linear molecular motors, whereas the one-dimensional angular algorithm (Eq. 1) is more suitable for control of rotary motors, in particular in combination with the use of bead pairs as a handle for applying torque to rotary molecular motors. In previous studies of linear molecular motors, independent x and y feedback control was implemented either in software (51) or by analog proportional-integral-derivative circuits (64). The spatial resolution achieved in those studies was higher than presented in this article, usually on the order of 1 nm, however, the 9-nm resolution of our AODs is adequate for the 1–10° angular resolution required for rotary molecular motors studies. The time resolution of our system is on the order of 1–2 ms, suitable for studies of F₁ and the bfm. Analog proportional-integral-derivative circuits for trapping laser control can offer higher time resolution, but lack the flexibility to implement various nonlinear algorithms and have therefore not been used in the system presented in this article. The control of our system is precisely clocked due to the use of a fast DSP, unlike in feedback systems implemented in software on the host computer. Faster DSP boards and AODs with faster response time are commercially available and would offer improved time and angle resolution if required.

Previous studies have used magnetic tweezers (29–31) and electrorotation (28,63) to apply torque to rotary molecular motors. Here we have explored the possibility of using optical tweezers and have addressed the technical difficulties of this method. The temporal and angular resolutions achieved here are improved compared to both magnetic tweezers and electrorotation. Calibration of the torque exerted by optical tweezers is in principle easier than that of the other techniques due to the greater reproducibility of the bead-pair handles compared to magnetic beads or tethered cell bodies. However, we have found considerable variation in the trap stiffness when holding bead pairs, which may require calibration for each bead pair studied in the future. A further advantage over electrorotation is that the technique places no special requirements on the conductivity of the medium, for example, allowing experiments in the relatively high ionic strengths that are suitable for study of sodium-driven flagellar motors (17).

There are several reasons why a bead pair serves as a better handle for micromanipulation with an optical trap than a single bead. Most obviously, the asymmetry of a bead pair indicates motor rotation more clearly than a single bead, which can rotate about any diameter without being detected by a position-sensitive detector. The extended lever arm of a bead pair increases the linear motion for a given angular motion, which enhances both the sensitivity of angular detection and the amount of torque that can be applied using a conventional optical trap. Furthermore, we have observed that a single 500-nm bead cannot be optically trapped to control the angle of the flagellar motor, due to the flagellar hook acting as a universal joint. Rotating bead pairs attached to the flagellar motor sometimes produced highly elliptical traces (data not shown), indicating either misalignment of the center of rotation with the QD, misalignment of the rotation axis with the microscope axis, or extra degrees of freedom. Rotating bead pairs attached to F₁ produce almost circular trajectories. For high-precision measurements of both rotary molecular motors it will be necessary to select motors with nearly circular trajectories.

The torque exerted on a motor via a bead pair in a linearly polarized optical trap can be written as T_trap = T_lever + T_shape + T_polarization, where T_lever is the combined effect of the linear force on the bead pair and the reaction force at the motor, T_shape is the alignment effect of a nonspherical trap on a nonspherical particle, and T_polarization is a torque acting to align the long axis of the bead pair with the polarization vector of the laser beam. Referring to Fig. 2 A to define x, y, and z axes, we can expect T_shape = (0, T_y,shape, 0), as single-beam optical traps are typically extended in the z-direction and particles align with their long axes parallel to the optical axis of the trap (41–43), and T_lever = (0, 0, −k_lever(θ_bp − θ_t)). When a bead pair attached to a molecular motor is held in feedback, the trap torque will balance the torque due to the bead-motor-surface link: T_trap = T_link. Considering the z-components we have

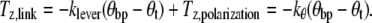(2)

In an ideal system, T_z,link would be dominated by the motor torque that we are trying to investigate, k_lever would be constant, and T_{z,polarization} would be negligible, in which case k_θ would also be a constant. In this case we would have

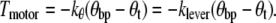(3)

In practice, however, T_z,link and k_θ may vary with θ_bp for the following reasons: 1), k_lever will vary with angle due to variations in laser intensity at different trap positions, differences between trap stiffness in x and y, and misalignment of each bead pair leading to different lengths of lever arm at different angles. 2), Whereas intuitively we might expect T_{z,polarization} to have a period of 180° in θ_bp, theoretical predictions show that higher periodicities might be possible depending on the shape and size of the particle (65). 3), Other than T_motor the most likely contributor to T_z,link is direct interaction between the bead pair and the surface, in parallel with the linkage via the motor. The angular dependence of this interaction is impossible to predict, may vary from bead to bead, and furthermore may depend upon T_y. Minimizing T_y by selecting flat-rotating “propeller” bead pairs (as discussed below) is expected to minimize this effect, and the observation of bead pairs performing free RBM indicates that T_z,link is negligible for many bead pairs in the absence of any trap torque. Regardless of the exact causes of angular variation in the trap torque, our measurements indicate that variation is considerable and not predictable, and that trap stiffness must be calibrated for each bead pair if absolute torques are to be measured.

There are two reasons to minimize the alignment torque, T_y. As well as the possible effect on T_z,link, as discussed above, T_y will be balanced by an opposing torque that consists of a vertical force acting on the motor multiplied by the lever-arm distance between the motor and a second point of contact between the bead and surface. The lever arm is likely to be very short, on the order of the size of the motor, and thus the force on the motor may be large even for relatively small T_y. T_y consists of T_y,shape and T_{y,polarization}, both of which depend upon the angle, φ (Fig. 2 A). As this angle increases, bead pairs change from vertically stacked beads, φ = 0°, to flat-rotating propellers, φ = 90°, whereas the radius of the circle described by the center of the outer bead increases from zero to the bead diameter (Fig. 2 B). At φ = 90° T_y is equal to zero (42,65,66), which is the reason for choosing flat-rotating propellers in our experiments. For bead pairs attached to the bfm or F₁, these are common. The height of a single 500-nm bead can be judged by eye with an accuracy of ∼30 nm, corresponding to ∼3° in φ. The accuracy in determining φ may be improved since we are comparing the image of the two adjacent beads (Fig. 2 B). Others have estimated T_y = ∼300 pNnm at φ = 87° for chloroplasts of radius 500 nm and length 2 μm (in a 1064-nm laser trap at 30 mW laser power (42)). Thus we might expect T_y on the order of tens of pNnm in our experiments. As well as the vertical force opposing T_y and the lateral force completing the couple T_lever, the motor may experience a radial force pulling the bead pair toward the center of the trap. In our experiments, the trap moves at a radius similar to the bead diameter, and therefore we expect small radial force, but whatever the actual values of the vertical and horizontal forces on the motor, the immediate resumption of spinning when the trap is shuttered illustrated in Fig. 5 A demonstrates that they are small enough not to damage F₁.

By contrast, our preliminary experiments on the bacterial flagellar motor indicate that damage to motors may be an important practical consideration when using the optical trap to investigate the motor. Laser exposure in the experiments illustrated in Fig. 5, A–C, was minimal, and is not expected to cause significant photodamage (54). The reductions in motor torque observed are therefore probably attributable to mechanical damage that inactivates individual torque-generating units, as seen in previous experiments in which electrorotation was used to apply external torque to the flagellar motor (63). For most of the cells we observed, significant damage occurred during the fine alignment procedure, indicated by a reduction in the speed of the free motor. The time it takes for fine alignment varies from cell to cell, but it is usually on the order of 1 min. In cases where the trajectory of the bead pair attached to the motor was almost circular the fine alignment procedure may not be necessary and might be omitted in the future. If the problem of mechanical damage can be solved it will be possible to determine the motor torque at each speed using Eq. 2, calibrating k_θ(θ_bp) for each bead pair. If so, the method of Fig. 5 C will allow measurement of the torque-speed relationship of the bfm under a wide range of different conditions, especially when the motor is driven backward or forward up to and beyond the zero torque speed, regimes that are not accessible without the application of external torque.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.