Energy transport in peptide helices

Abstract

We investigate energy transport through an α-aminoisobutyric acid-based 3₁₀-helix dissolved in chloroform in a combined experimental-theoretical approach. Vibrational energy is locally deposited at the N terminus of the helix by ultrafast internal conversion of a covalently attached, electronically excited, azobenzene moiety. Heat flow through the helix is detected with subpicosecond time resolution by employing vibrational probes as local thermo meters at various distances from the heat source. The experiment is supplemented by detailed nonequilibrium molecular dynamics (MD) simulations of the process, revealing good qualitative agreement with experiment: Both theory and experiment exhibit an almost instantaneous temperature jump of the reporter units next to the heater which is attributed to the direct impact of the isomerizing azobenzene moiety. After this impact event, helix and azobenzene moiety appear to be thermally decoupled. The energy deposited in the helix thermalizes on a subpicosecond timescale and propagates along the helix in a diffusive-like process, accompanied by a significant loss into the solvent. However, in terms of quantitative numbers, theory and experiment differ. In particular, the MD simulation seems to overestimate the heat diffusion constant (2 Ų ps⁻¹ from the experiment) by a factor of five.

Proteins are molecular machines that need to transport energy to work and function. Mainly, this occurs in two forms: Propagation of conformational changes and removal of excess heat. For example, consider a folding protein that undergoes a conformational transition to a state of lower energy. The transition may be facilitated, e.g., through a local conformational rearrangement (e.g., formation of a hydrogen bond) that in turn triggers further structural changes (e.g., by a zipping mechanism). This propagation of conformational change is directly associated with a transport of energy along the protein backbone. To localize in the state of lower energy, the excess energy of the protein must be removed efficiently and rapidly. Excess heat must also be dissipated in the case of a chemical reaction, because proteins function in narrow temperature ranges. Another example in which both kinds of energy transport occur are photoproteins such as rhodopsins. On one hand, the energy of the photon is used to trigger a conformational rearrangement, but, on the other hand, the excess energy needs to be removed. Because the functionality of a protein is directly associated with its structure, one may expect that energy transfer mechanisms are also related to structural motifs such as α-helices or β-sheets, both of which are stabilized by hydrogen bonds. In particular, helices often span the whole protein, giving rise to the speculation that they actually channel vibrational energy through the biomacromolecule (1).

To study energy transport from the theoretical point of view, a commonly used approach tries to transfer the theory of heat diffusion of glasses onto the length scale of a protein (2–4). Another very direct and intuitive approach is to run nonequilibrium molecular dynamics (MD) simulations, depositing energy into one vibrational mode and following its flow through the protein directly as a function of time (5–10). On the experimental side, the study of energy and heat transport is well established for bulk systems (solids, glasses, or liquids) (11). For proteins, however, essentially nothing is known about heat diffusion from experiment. We are aware of only very few experimental studies (12–16), which all investigated the energy flow in heme proteins. However, it has been argued later that heat transport from the heme into the surrounding solvent water does not occur through the protein in this case but through the propionate side chain of the heme molecule that connects it directly to the protein surface (8, 17). In systems other than proteins, energy transport phenomena have been measured, for example, through bridged azulene-anthracene compounds (18), small molecules in solution (19), or model membranes (20).

Employing a combination of peptide engineering, time-resolved infrared absorption spectroscopy, and nonequilibrium MD simulations, we set out to study energy transport specifically along peptide helices as one of the most important structural elements of proteins. To that end, we synthesized a molecule (Fig. 1a) that consists of a stable helix with a dye molecule attached covalently, the latter undergoing ultrafast internal conversion and thereby locally depositing energy.

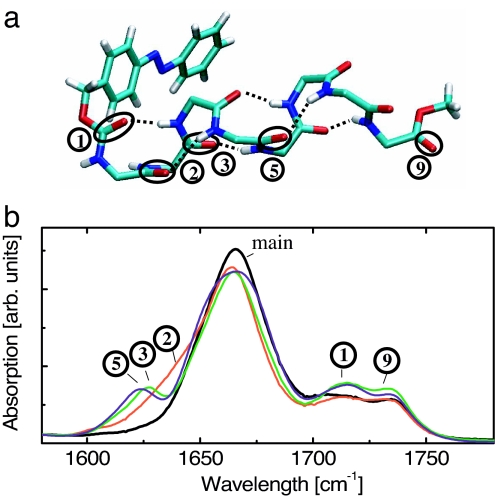
Fig. 1.

Structure and steady-state spectroscopy. (a) X-ray structure of PAZ-Aib-Ala-(Aib)₆-OMe (molecule A, only the backbone is shown). The tags 1 to 9 refer to the corresponding absorption bands in b and count CO groups with increasing distance from the azobenzene moiety. (b) FTIR absorption spectra of the ¹³C-unlabeled reference molecule (PAZ-Aib-Ala-Aib₆-OMe, black line), and those of the ¹³C-labeled peptides PAZ-Ala*-Aib₇-OMe (red), PAZ-Aib-Ala*-Aib₆-OMe (green), and PAZ-Aib₃-Ala*-Aib₄-OMe (blue).

In designing the helix, we were guided by the following considerations: Typical α-helices from C^α-trisubstituted α-amino acids in solution are flexible, and need on the order of 20 amino acids to become marginally stable (21). We therefore decided to use the C^α-tetrasubstituted α-amino acid α-aminoisobutyric acid (Aib), which forms exceptionally stable 3₁₀-helices, even in a relatively short sequence of 8 aa (22–24). 3₁₀-helices are less common but are found in globular proteins (25). Aib-based 3₁₀-helices dissolve in the apolar solvent chloroform, which minimizes potential loss of the heat flow into the surrounding solvent and moreover mimics the hydrophobic environment in the interior of a protein.

As heater, we chose azobenzene because it undergoes ultrafast internal conversion (cis and trans isomerization) on a 200-fs timescale (26). The azobenzene moiety 4-(phenyldiazenyl-benzyloxycarbonyl) (PAZ) was introduced in the N^α-protecting group (27, 28) of the peptide chain, with electronic properties (i.e., UV-VIS spectra, isomerization yields, and rates) that are essentially the same as that of unsubstituted azobenzene. To give an idea about the expected effects, one may assume a Boltzmann distribution of the photon energy (≈3 eV) over all vibrational degrees of freedom of the azobenzene compound, in which case one would estimate a local temperature of 1,150 K right after the photoreaction. That huge temperature gradient is then equilibrating either along the helix or into the solvent.

To follow the energy flow along the helix, we make use of vibrational bands shifting in frequency upon heating of their surrounding. This effect has been studied in detail in ref. 29, where it has been shown that vibrational modes can be used as local thermometers. In the present study, we employ the CO groups of the peptide backbone as local thermometers. To obtain spatially localized and spectroscopically separated vibrational transitions, we isotope-label these ¹³CO groups, frequency downshifting it by ≈30 cm⁻¹, and thereby singling out one site from the remainder. Placing the isotope label at different positions in the helix, we can measure the local temperature at various distances from the heat source as a function of time. Because ¹³C-Alanine (Ala) is more readily available commercially than ¹³C-Aib, we used the former for isotope labeling. Disturbing the Aib₈ sequence by one residue (Ala), however, should not destabilize the 3₁₀-helix significantly (23, 24, 30) (see Structural Characterization).

The experimental studies are accompanied by extensive nonequilibrium MD simulations in explicit solvent. After validation of the computational methods through the comparison to experiment, the simulations are able to draw a microscopic picture of the molecular processes underlying energy transport in peptides.

Structural Characterization

The terminally protected Aib₈ sequence is known to be folded in a fully developed 3₁₀-helical structure in chloroform solution (23). In this work, we have examined the preferred conformation of the three host/guest octapeptides PAZ-Ala*-Aib₇-methoxy (OMe), PAZ-Aib-Ala*-Aib₆-OMe and PAZ-Aib₃-Ala*-Aib₄-OMe. X-ray diffraction revealed for the crystal structure of PAZ-Aib-Ala-(Aib)₆-OMe two independent peptide molecules (A and B) in the asymmetric unit [see Fig. 1a and supporting information (SI) Fig. 6]. Both are regular 3₁₀-helices, stabilized by six consecutive, i + 3 → i N-H … OC intramolecular H-bonds. The two independent molecules differ by their helical screw sense, right-handed for molecule A and left-handed for molecule B, an uncommon, but not unique, observation for an Aib-based sequence with a single internal chiral residue (31).

To validate that the 3₁₀-helical structure is maintained in structure-supporting solvents (chloroform and 2,2,2-trifluoroethanol), FTIR absorption, ¹H NMR, and CD techniques have been applied. The FTIR absorption spectra in the N-H stretching region of all three peptides in CDCl₃ solution (SI Fig. 7) are similar, showing a weak band at ≈3,425 cm⁻¹ (free N-H groups) (23) and a very intense band near 3,325 cm⁻¹ (hydrogen bonded N-H groups). Because a change in peptide concentration (from 1.0 mM to 0.1 mM) does not significantly modify the spectra, the observed hydrogen bonding can be safely assigned to the intramolecular type. The ratios of the integrated intensity of the band of hydrogen bonded N-H groups to that of free N-H groups for the three peptides is in accordance with previously reported results for the 3₁₀-helical Aib₈ peptide (23).

The results of the ¹H NMR titrations in CDCl₃ solution upon addition of the hydrogen bonding acceptor solvent dimethylsulphoxide (SI Figs. 8–10) clearly indicate that two NH protons for each octapeptide are exposed to the solvent, whereas the remaining six NH protons are solvent protected because of hydrogen bonding. One of these NH protons (that at highest field) is assigned to the N-terminal N(1)H proton by virtue of its urethane character (23). In PAZ-Aib-Ala*-Aib₆-OMe, the second solvent exposed NH proton is easily attributed to Ala* at position 2 on the basis of its different multiplicity. These ¹H NMR properties are those expected for peptides adopting a regular 3₁₀-helical structure (23).

As a typical example, the CD spectrum of PAZ-Aib-Ala*-Aib₆-OMe in 2,2,2-trifluoroethanol solution is reported in SI Fig. 11. The positions of the two negative Cotton effects (205 nm, very strong and 225 nm, weak) and the ratio of their intensities (0.25) are those expected for a 3₁₀-helix (32).

The potential destabilizing effect of a single Ala residue included in an Aib host peptide was also studied by comparing two 40-ns equilibrium MD simulations of PAZ-Aib₈-OMe and PAZ-Aib₃-Ala*-Aib₄-OMe. As an example, SI Fig. 12 shows the distribution of the number n_HB of intramolecular hydrogen bonds in the two cases. Although PAZ-Aib₈-OMe shows more conformations with the maximum number of possible intramolecular hydrogen bonds (n_HB = 6), on average, we find similar hydrogen bonding (〈n_HB〉 = 4.2 and 3.6) for PAZ-Aib₈-OMe and PAZ-Aib₃-Ala*-Aib₄-OMe, respectively.

Experimental Results

Fig. 1b shows the stationary FTIR absorption spectrum in the CO stretching region of the ¹³C-unlabeled reference molecule (PAZ-Aib-Ala-Aib₆-OMe), together with those of the ¹³C-labeled peptides PAZ-Ala*-Aib₇-OMe, PAZ-Aib-Ala*-Aib₆-OMe and PAZ-Aib₃-Ala*-Aib₄-OMe, respectively. The ¹³C-unlabeled peptide shows three bands: the dominating “main band” at 1,665 cm⁻¹, which is composed of all equivalent CO groups in the helix, and two chemically different CO groups that are split off from the main band, i.e., the urethane group at 1,715 cm⁻¹ (band 1), which links the azobenzene moiety to the peptide helix, and the ester CO band at 1,734 cm⁻¹ (band 9) from the C-protecting group. The¹³C-labeled peptides PAZ-Aib-Ala*-Aib₆-OMe and PAZ-Aib₃-Ala*-Aib₄-OMe each exhibit one additional red-shifted band at ≈1,625 cm⁻¹ (bands 3 and 5, respectively), whereas the corresponding group in PAZ-Ala*-Aib₇-OMe reveals only a barely resolved shoulder (band 2) on the low-frequency side of the main band.

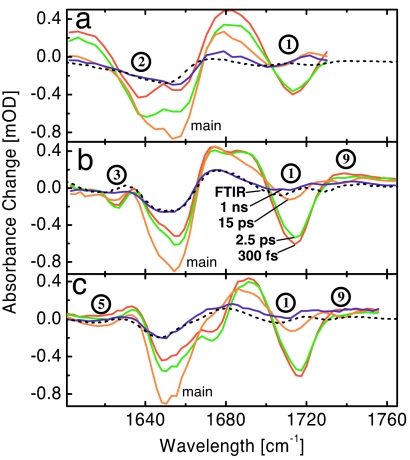
Fig. 2 presents the UV-pump-IR-probe transients of the various samples at delay times from 300 fs to 1 ns. All vibrational modes do respond to the photo-excitation, albeit with different time dependencies. At the earliest delay time of 300 fs, band 1, which is closest to the azobenzene moiety, responds with the largest signal. This signal decays relatively quickly (Fig. 3), whereas the main band leads to the dominating response 15 ps after excitation. The main band signal again decays partially until 100 ps (Fig. 3a Inset) and then stays more or less constant until 1 ns. Its shape does not change very much during this time (compare 15-ps with 1-ns spectra in Fig. 2). The various labels (bands 2, 3, and 5 in Fig. 2 a, b, and c, respectively) respond with relatively small, but distinctive, derivative-like signals of decreasing intensity as the distance from the heater is increased. Also, band 9 (the ester C-protecting group) reveals a tiny derivative-like response.

Fig. 2.

Transient spectra. Pump-probe signals of PAZ-Ala*-Aib₇-OMe (a), PAZ-Aib-Ala*-Aib₆-OMe (b), and PAZ-Aib₃-Ala*-Aib₄-OMe (c) at various delay times (300 fs, red; 2.5 ps, green; 15 ps, orange; 1 ns, blue) after pumping the cis-azobenzene moiety with a 425-nm pulse, compared with a stationary temperature induced difference spectra (black dotted) corresponding to a temperature jump of ≈0.5 K.

Fig. 3.

Time traces. Time dependencies of the bleach intensity (with opposite sign as in Fig. 2) of bands 1 to 9 and the main band, of PAZ-Aib-Ala*-Aib₆-OMe (a) and PAZ-Aib₃-Ala*-Aib₄-OMe (b) (gray lines). The black lines show global fits according to a simple kinetic scheme (see Discussion). The inset in a shows the recovery of the main band on a longer timescale together with that of band 9 (the latter being up-scaled by a factor of 7).

When cis-azobenzene is optically excited to the n → π* transition by a 425-nm photon, it isomerizes toward the trans configuration within <200 fs with ≈50% quantum yield (26). Thereby, it will deposit a certain fraction of the photon energy (≈3 eV) into its vibrational degrees of freedom. The energy dumping will be relatively nonspecific, and, according to the MD simulations discussed below, thermalizes on an ultrafast subpicosecond timescale. There are two major routes where the energy, or heat, can go: into the solvent or along the helix. Indeed, we do see the largest signal at early delay times from the CO group 1 closest to the source of the “heat” (Fig. 2). The signal predominantly relates to a red shift of band 1, i.e., a negative bleach at the original position of the band and a relatively broad positive band red shifted from that position. We assign this signal to the local temperature at the N terminus of the helix. Even at the highest conceivable temperatures reached in this experiment, a CO mode with 1,600–1,700 cm⁻¹ will not directly be excited according to a Boltzmann factor of e^−ℏω/kBT. However, thermal excitations of lower frequency modes that are in spatial vicinity to a specific reporter CO group will cause anharmonic frequency shifts of the latter, an effect that has been studied in detail in ref. 29.

The interpretation of the signal of band 1 as a local “temperature” is supported by its 7-ps decay time shown in Fig. 3 a and b, which roughly coincides with what is known as the typical cooling time in the solvent chloroform (33). Cooling of organic dye molecules in various solvents has been studied extensively over the past decades (33–35). In particular, it has been established that the cooling time is essentially a solvent property, which is more or less independent on the particular solute molecule.

Combining these two pieces of evidence, we assign a bleach and/or shift signal associated with a 7-ps decay component as heat in the vicinity of the corresponding CO group. Apart from unit 1, the only other group that shows such a 7-ps decay component is unit 3 (Fig. 3a). However, the way how unit 3 builds up is different: After an instantaneous rise, it continues to grow until it peaks delayed after ≈2.5 ps. We do not see any 7-ps decay component further away from the heater for band 5 in PAZ-Aib₃-Ala*-Aib₄-OMe or band 9 in either of the samples.

Hence, we do observe a propagation effect. If we assume that the signal amplitude is roughly proportional to the vibrational energy present at a particular position (29), one would conclude that the temperature jump at position 3 is ≈1/3 of that at position 1, whereas the temperature jump at position 5 or further away is immeasurably small. The temperature jump at position 2 is lying somewhere in between that of 1 and 3 (because of spectral overlap we do not attempt to quantify the value), indicating that energy flow occurs through the backbone and not through the hydrogen bond between unit 1 and 3.

The main band responds in a distinctly different way to heating of the molecule. The spectral response between 15 ps and 1 ns is dominated by the main band which reveals a blue shift, i.e., a negative bleach at the original position of the band and a positive band blue shifted from that position. These late-delay-time spectra strongly resemble stationary temperature induced difference spectra (Fig. 2, dotted lines)^‖, suggesting that we are left with the response to an elevated temperature after ≈15 ps. The temperature rise leads to an overall weakening of the hydrogen bonds of the helix and, in turn, results in a blue shift of the related CO vibrators (36). We associate the partial decay of this signal with a 35-ps time constant (Fig. 3a Inset) to heat diffusion from the first solvation shell into the bulk solvent, which occurs on a characteristic timescale of a few tens of picoseconds (37). The CO group furthest away from the chromophore (band 9) and band 5 in PAZ-Aib₃-Ala*-Aib₄-OMe exhibit a kinetics that closely mimics that of the main band (Fig. 3a Inset). Hence, in contrast to unit 1 to 3, any group further away from the heater sees only a secondary effect because of partial destabilization of the hydrogen bonds.

Computational Results

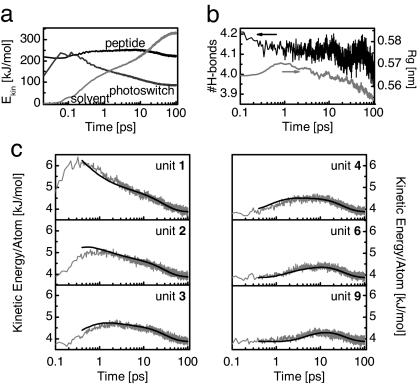
To guide the interpretation of the experiments and obtain a microscopic picture of the molecular processes underlying energy transport in peptides, we have performed nonequilibrium MD simulations of the photoinduced dynamics. Although the quantitative description of these processes in general requires a quantum-mechanical modeling (4, 10), a simple classical approach to study energy transport (9) is to consider the time evolution of the kinetic energy in various parts of the molecular system (Fig. 4a). After the photoexcitation at time t = 0, the kinetic energy is deposited into the azobenzene photoswitch within <0.1 ps. While the excitation of the photoswitch decays on a picosecond time scale, its energy is transferred to the Aib peptide (30%) and directly to the solvent (70%). The peptide energy rises within 0.3 ps and remains approximately constant up to 10 ps, before it decays with an ≈20-ps time constant. The solvent energy E_solv(t)** rises with time constants 0.5 ps and ≈20 ps, where the shorter time scale reflects the initial momentum transfer of the isomerizing photoswitch to its surrounding solvent molecules. After the thermalization of the photoinduced energy, the 20-ps time scale of E_solv(t) accounts for the subsequent cooling of the PAZ-Aib₈-OMe peptide.

Fig. 4.

Time evolution of the photoinduced dynamics of PAZ-Aib₈-OMe from the MD simulation. (a) Total kinetic energy of the Aib₈ peptide (black), the photoswitch (gray) and the solvent (light gray). (b) Mean number of 3₁₀-helix hydrogen-bonds (black, left scale) and radius of gyration of the Aib₈ peptide (gray, right scale). (c) Mean kinetic energy of selected residues. The black lines show global fits according to the kinetic model described in Discussion.

The time evolution of the main band (initial rise with a peak at ≈15 ps and recovery on a 35-ps time scale) was interpreted above to be associated with a transient weakening and reformation of the hydrogen bonds, thereby destabilizing the helix for some time. To investigate this issue, Fig. 4b shows the time evolution of the average number of stabilizing 3₁₀-helix hydrogen bonds n_HB. On average, photoexcitation causes only a small change of n_HB of ≈0.2. Similarly, the peptide radius of gyration, a measure of the size of the peptide, virtually remains constant (Fig. 4b). We therefore conclude that the photoexcitation does not lead to significant conformational changes of the peptide, and that the transient effect we observe in the experiment relates to this small change of n_HB.

To elucidate the energy transfer along the peptide chain, Fig. 4c displays the time evolution of the mean kinetic energy for most of the peptide groups. The time-delayed rise of these energies nicely illustrates the transport of energy (or heat) along the peptide backbone. Let us compare the simulated and experimentally observed energy transports along the peptide backbone. The kinetic energy of unit 1 (the linker unit to the photoswitch) reaches its peak at 0.3 ps, which nicely agrees with the experimental finding that unit 1 takes up substantial energy within the time resolution (0.2 ps). Unit 2 receives ≈50% of the energy from unit 1, and unit 3 receives 35% within 1 ps. According to the simulation, the terminal unit 9 still receives a small (20%) amount of the excess energy because of the photoexcitation, but this effect is not measurable in the experiment.

Several tests were pursued to learn more about the mechanism of energy transfer. First, we performed two nonequilibrium simulations where the initial states of the peptide were chosen to represent conformations with high (4.7) and low (3.5) average number n_HB of stabilizing 3₁₀-helix hydrogen bonds, respectively. Comparing the time evolution of the mean kinetic energy of each of the Aib residues, SI Fig. 13 reveals that the energy transfer is essentially identical in both cases. Moreover, the time evolution of the kinetic energy including only the CONH atoms of the pepide unit (as done in Fig. 4c) was found to be quite similar to the case when all atoms were taken into account (see SI Fig. 14). In agreement with experiment, these findings indicate that the transport of energy is not primarily mediated through intramolecular hydrogen bonds or side-chain atoms but rather proceeds through the backbone atoms.

Discussion

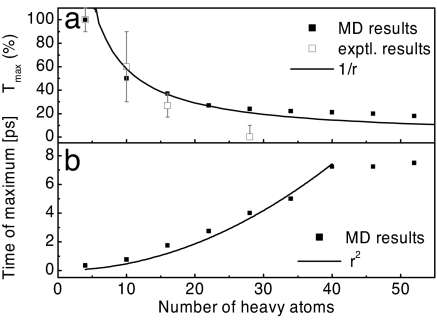
To discuss the molecular mechanisms underlying the energy transport, we start with the analysis of the computational data and plot the maximal amplitudes and the peak times of the transferred energy as a function of the number of heavy atoms along the peptide chain (Fig. 5). The number of heavy atoms, relevant for thermal properties such as heat capacity and thermal conductivity, is used as a measure for the distance from the heater. Considering Fig. 5 together with Fig. 4a, we find that the energy transport occurs in two stages, that is, an initial stage for times t ≲ 1 ps and distances r ≲ 10 heavy atoms and a subsequent stage for larger times and distances. In the initial phase, two competing processes occur. Because the photoisomerizing azobenzene moiety essentially bumps into the surrounding solvent molecules, we observe an ultrafast (0.5-ps time scale) and efficient (70% of the excess energy) heat transport into the solvent (Fig. 4a). At the same time, 30% of the excess energy arrives within only 0.1 ps at CO group 1, that is, at distances of four heavy atoms or 2 Å. Because this distance per time roughly corresponds to the speed of sound of about v_s ≈ 20 Åps⁻¹, we may refer to the process as “ballistic.” We note that this ballistic transport is restricted to distances shorter than ≈10 heavy atoms, where the peptide chain may be considered as relatively rigid. (For a completely rigid molecule, the transfer of conformational change would be instantaneous.) For longer distances, the increasing flexibility of the peptide chain hampers a direct ballistic transfer. In fact, because the energy of the peptide remains approximately constant for times 0.3 ps ≲ t ≲ 10 ps (Fig. 4a), we find that the photoswitch and the peptide are thermally decoupled after 0.3 ps. To transport energy over longer distances, delocalized low-frequency modes are needed (2–4) that exist along the uniform peptide backbone, but presumably not between peptide and the azobenzene moiety.

Fig. 5.

MD results. Maximal amplitudes (a) and peak times (b) of the energy transferred to residue Aib_n from the raw MD data, plotted as a function of the number of heavy atoms along the peptide chain, together with 1/r and r² fits. In a, the experimental results are included for comparison (open squares).

Assuming thermal decoupling, the energy distribution of the atoms of unit 1 at t ≈ 0.3 ps can be considered as the initial state of the subsequent energy transfer along the peptide chain. Interestingly, the latter is well fitted by a Maxwell distribution for 500 K, that is, unit 1 is thermalized at ultrafast times. Starting with a thermalized initial state and conserving energy, the second stage, that is, the subsequent energy transfer along the peptide chain, may be described by a 1D diffusion process. Indeed, the transferred energies and peak times shown in Fig. 5 exhibit the expected 1/r and r² behavior, respectively. As this model assumes energy conservation, however, the fits deteriorate for times ≳10 ps and distances ≳40 atoms, reflecting the dissipation of the peptide energy into the solvent.

To obtain a more realistic model of the diffusional transport along the peptide chain, we have constructed a simple rate-equation model which assumes that (i) each peptide unit exchanges energy with its nearest neighbor according to a (forward and backward) rate constant k_p and (ii) each peptide unit loses energy to the solvent with the rate k_s. A global fit of the time traces in Fig. 4c yields the relaxation times 1/k_p = 0.4 ps and 1/k_s = 18 ps. Apart from the ultrafast energy rise of the first few units, the fits match very well the simulation data, thus suggesting that the simple kinetic model is appropriate.

Comparing theoretical and experimental results, we find a good overall agreement. Also in the experiment we observe an instantaneous (within temporal resolution) rise of the temperature signal for units 1-3, reporting on the impact of the switching azobenzene moiety that seems to perturb deeper into the helix as in the MD simulation (i.e., the instantaneous contribution to the rise of band 3 is larger in the experiment). Subsequently, energy propagates through the helix but drops very quickly with increasing distance from the heater (Fig. 5a, open squares). Applying the above described heat propagation model to the experimental results, we obtain relaxation times 1/k_p = 2 ps and 1/k_s = 7 ps, respectively (see fits in Fig. 3). The small deviation between fit and the experimental data at times >15 ps might reflect an elevated temperature of the solvent, and hence back-transfer of heat from the solvent to the molecule, which, in part, might stem from heat transferred directly into the solvent during the isomerization process of the azo-moiety. In this case, a power-law dependence would be expected for the final decay. However, experimental uncertainties in determining offsets do not allow us to discuss this effect. In ongoing work, we are currently investigating the temperature dependence of heat transport, providing evidence that viscosity affects in particular the initial impact event.

Compared with experiment, the MD calculations thus overestimate the peptide transport rate by a factor of five but underestimates the cooling rate by a factor of 2.5. As discussed elsewhere (9), the latter effect is most likely caused by the rigid force-field model used for the chloroform solvent. (Employing a flexible model of the solvent adds more degrees of freedom and therefore increases the heat capacity and the ability to cool the solute, albeit at the cost of other problems such as the classical description of high-frequency modes.) When the propagation rates are related to the heat diffusivity D = k_pΔx² [with Δx ≈ 2 Å being the helical translation per residue for a 3₁₀-helix (25, 30)], we obtain D = 2 and 10 Ų ps⁻¹ from experimental and calculated data, respectively. Our nonequilibrium MD result agrees well with results from a comparable simulation of cooling of a protein [7 Ų ps⁻¹ (6)], as well as with recent quantum-classical calculations [≈20 Ų ps⁻¹ (2–4)]. The latter were based on an equilibrium normal-mode analysis employing a similar MD force field, augmented with a Golden Rule-type modeling of energy relaxation using cubic anharmonicities. This result indicates that the significant deviation between theory and experiment is less a matter of quantum effects but is rather caused by the empirical potential-energy models used. Another indication for the minor importance of quantum effects is that the deviation is virtually independent of whether the peptide bond lengths are constrained (thereby mimicking quantum effects) or not in the MD simulation.

In fact, it is well known from peptide folding simulations that the calculated folding transition temperature is typically well above (≈30%) the experimental value, that is, the force field is “too rigid” at high temperature (see, e.g., ref. 38). Apart from incomplete sampling, this observation appears to be a consequence of neglecting polarizability and many-body interactions and the fact that force field parameters are derived for room temperature rather than for the high temperature range. The problem considered here is similar in that the typical temperature of the peptide is between 400–500 K during the first 10 picoseconds (see Fig. 4c) and that a too rigid force field may enhance the transport of energy. As one may expect a better agreement of theory and experiment at lower temperatures, it would be interesting to extend our studies to low-energy excitation.

Conclusions

Pursuing a joint experimental-theoretical investigation, we have drawn a molecular picture of the energy transfer processes in a photoactivated peptide. Following ultrafast cis–trans photo isomerization of the azobenzene moiety, the energy transfer was found to occur in the following two stages. (i) Initially, 70% of the excess energy is dissipated into the solvent on a 0.5-ps time scale. The high efficiency of this process is crucial for biomolecules to survive photoexcitation or to remove excess heat of chemical reactions. The remaining 30% of the energy is transferred in a ballistic way to the beginning of the peptide helix, where it is thermalized within only 0.3 ps. (ii) The subsequent energy transfer along the peptide chain was found to be well described by a 1D diffusion process with a heat diffusivity of 10 Ųps⁻¹, as contrasted to the experimental value of 2 Ųps⁻¹. Achieving the propagation of conformational changes, this process is crucial for the functionality of the biomolecule.

Solitonic effects, if at all existent, apparently do not play a role in stabilizing and funnelling energy through the helix efficiently, as is has been speculated quite some time ago by Davydov (1). The heat propagation rate along the helix only slightly (by a factor of 3–4) exceeds that into the solvent. This finding seems surprising, because covalent and hydrogen bonds exist within the helix, whereas coupling to the surrounding was reduced as much as possible by the choice of an apolar solvent. However, low frequency modes dominate heat transport, because they tend to delocalize over large distances (2–4). Apparently, even the weak Van der Waals interactions with the solvent give rise to intermolecular solvent-peptide modes in the right frequency range, that efficiently transport energy into the solvent. Currently, it is not clear how heat transfer between adjacent helices would occur in a larger protein. Nevertheless, the present study provides the first direct measurement of the heat diffusion constant of a peptide helix that is considered an important structural element of proteins.

Materials and Methods

Synthesis.

Deuterated PAZ-Aib-OH was synthesized by nitrating toluene-D₈ to p-nitrotoluene, oxidizing to p-nitrobenzoic acid, reducing with zinc to p-aminobenzoic acid, and then making the methyl ester using methanol and thionyl chloride. Reduction of the ester with lithium-aluminium-deuteride (39) leads to the full deuterated p-aminobenzyl alcohol. Nitrosobenzene-D₅ was obtained by reduction of nitrobenzene-D₅ as described in ref. 40. Coupling these two deuterated compounds and covalently linking the resulting alcohol to l-Ala* and Aib was performed in the same way (using PAZ-Cl) as reported in refs. 27 and 41. Peptide synthesis was performed in solution by activating the carboxyl function with 1-(3-dimethylaminopropyl)-3-ethylcarbodiimide and 7-aza-1-hydroxy-1,2,3-benzotriazole (42). Details of the synthesis and characterization are reported in the SI Text.

Time Resolved Experiments.

The peptides were investigated by UV-pump-IR-probe spectroscopy exciting cis-azobenzene at a wavelength of 425 nm (26), and probing the amide I region with an IR-probe pulse centered at 1,680 cm⁻¹ (spectral width 200 cm⁻¹). The probe pulse was frequency dispersed in a spectrometer and imaged onto a 64 channel IR array detector (or a 32 channel IR array detector in case of Fig. 2a) covering the total region of CO vibrations. The time resolution of the apparatus was 200 fs. The sample was dissolved in CHCl₃ at a concentration of typically 10 mM, circulated in a closed cycle CaF₂ flow cell with optical path length of 100 μm, and continuously irradiated with continuous wave-light at 320 nm (FWHM 70 nm) from a properly filtered Hg-lamp to accumulate the cis species to ≈80%.

Computational Methods.

All simulations were performed with the GROMACS program suite (43), using the GROMOS96 force field 43a1 (44) to model the PAZ-Aib₈-OMe peptide and the rigid all-atom model of ref. 45 to describe the chloroform solvent. Additional force field parameters for the azobenzene unit were derived from density functional theory as described in ref. 46. Starting with a 3₁₀-helical conformation, the PAZ-Aib₈-OMe peptide was placed in an octahedral box containing ≈700 chloroform molecules. After energy minimization, the system was simulated for 40 ns at NTP equilibrium conditions (1 atm, 300 K). Employing the same protocol, we also performed an equilibrium simulation of the peptide PAZ-Aib₃-Ala*-Aib₄-OMe. From the equilibrium trajectory of PAZ-Aib₈-OMe, 800 statistically independent conformations were obtained for the subsequent nonequilibrium simulations.

To model the laser-induced photoisomerization process, we use a minimal model for the corresponding potential-energy surfaces that diabatically connects the excited-state S₁ of the cis isomer with the ground state S₀ of the trans isomer (47). The photoexcitation of the system by an ultrafast laser pulse is mimicked by instantly switching from the ground-state NN torsional potential to the excited-state potential. Following this nonequilibrium preparation at time t = 0, the system isomerizes along an excited-state NN potential within ≈0.2 ps. After isomerization (i.e., for times ≥ 0.5 ps), the NN torsional potential is switched back to its ground state form, and a constant-energy MD simulation is performed up to 100 ps. Following the nonequilibrium simulations, the time-dependent observables of interest are obtained via an ensemble average over 800 equilibrium conformations.

Abbreviations

Aib

α-aminoisobutyric acid

Ala

Alanine

MD

molecular dynamics

OMe

methoxy

PAZ

4-(phenyldiazenyl-benzyloxycarbonyl).