Risky prey behavior evolves in risky habitats

Abstract

Longstanding theory in behavioral ecology predicts that prey should evolve decreased foraging rates under high predation threat. However, an alternative perspective suggests that growth into a size refuge from gape-limited predation and the future benefits of large size can outweigh the initial survival costs of intense foraging. Here, I evaluate the relative contributions of selection from a gape-limited predator (Ambystoma opacum) and spatial location to explanations of variation in foraging, growth, and survival in 10 populations of salamander larvae (Ambystoma maculatum). Salamander larvae from populations naturally exposed to intense A. opacum predation risk foraged more actively under common garden conditions. Higher foraging rates were associated with low survival in populations exposed to free-ranging A. opacum larvae. Results demonstrate that risky foraging activity can evolve in high predation-risk habitats when the dominant predators are gape-limited. This finding invites the further exploration of diverse patterns of prey foraging behavior that depends on natural variation in predator size-selectivity. In particular, prey should adopt riskier behaviors under predation threat than expected under existing risk allocation models if foraging effort directly reduces the duration of risk by growth into a size refuge. Moreover, evidence from this study suggests that foraging has evolved over microgeographic scales despite substantial modification by regional gene flow. This interaction between local selection and spatial location suggests a joint role for adaptation and maladaptation in shaping species interactions across natural landscapes, which is a finding with implications for dynamics at the population, community, and metacommunity levels.

The growth–predation risk tradeoff constitutes one of the more successful and generalizable predictions in ecology (1–3). This tradeoff pits the fitness benefits of foraging to gain resources for growth against the fitness costs of increased predation risk associated with active foraging. Most prey individuals are expected to decrease foraging activity when faced with intense predation risk (4, 5), especially if prey can compensate for reduced feeding opportunities by foraging more during future low-predation risk intervals (6). Empirical evidence suggests that prey frequently decrease foraging when presented with reliable cues of predation risk (1, 7, 8). However, multiple exceptions to this general pattern have been observed (9–12). One possible explanation for these counterexamples is that they represent cases where prey can reduce the duration of predation risk through foraging and growth into a large body size (13, 14). When a predator's gape or hunting apparatus constrains its capture of large prey items, the rapid growth that can result from more active foraging enables prey individuals to enter a refuge from predation at a large body size (15–17). Hence, a prey size refuge can alter the balance of costs and benefits in the foraging–predation risk tradeoff and can favor elevated foraging despite short-term increases in predation risk (16, 18). If generally true, then the evolution of divergent feeding strategies can be predicted based on variation in predator size-selectivity across landscapes and the prey's capacity for rapid growth.

Evidence for the adaptation of foraging rates in response to variable predator size-selectivity would provide a particularly strong test of this prediction (15, 19). Across natural landscapes, prey commonly face size-selective predators that differ in the maximum prey size consumed (e.g., ref. 19). When gene flow is limited by physical barriers or isolation by distance, prey foraging rate is expected to evolve to match the specific predation and environmental contexts of each population (9, 20, 21). The degree to which a population is adapted or maladapted to its habitat often depends on selection intensity and gene flow (22–24). Depending on its rate, gene flow can facilitate local adaptation by supplying new genetic variation or inhibit adaptation by swamping existing variation with less fit alleles (25). The relative matching between prey behavior and predator selection could play an important role in structuring species interactions and emergent community properties (26, 27).

Here, I assess the contributions of local selection and gene flow to interpopulation differences in prey foraging and growth rates and their consequences for the survival of spotted salamander prey (Ambystoma maculatum) under threat from predatory marbled salamanders (Ambystoma opacum). A. opacum adults breed in temporary ponds in the fall, and their predaceous larvae hatch and develop during winter. In contrast, A. maculatum adults breed in temporary ponds in the spring. Divergent breeding times allow for A. opacum larvae to grow to a size sufficient to prey upon hatching A. maculatum larvae. Field observations suggest that A. opacum larvae strongly decrease A. maculatum's early survival, but have weaker effects on their survival later in the season. A. opacum larvae are gape-limited on A. maculatum larvae and induce selection for larger A. maculatum body size (28). Hence, evidence suggests that A. maculatum eventually grow to a body size that prevents their capture by gape-limited A. opacum larvae.

Prior experiments have demonstrated genetically determined growth rates among prey from different geographic regions (28). In these experiments, larvae from regions with higher A. opacum risk grew more rapidly, suggesting the possible adaptation of prey growth rates to a regionally abundant gape-limited predator. However, it remains unclear whether regional trait patterns reflect the cumulative responses of locally adapted populations or a generalized response maintained across the region regardless of local predator heterogeneity. A demographic model parameterized for this predator–prey system suggests that intense gape-limited predation risk can select for higher relative prey foraging and rapid growth rates across a gradient from low to high gape-limited predation risk, while keeping gape-unconstrained predation risk constant (29). In the absence of strong gape-limited predation risks, slow growth rates are expected to evolve as a balance between a growth-related gain in fecundity and a growth-related fitness cost from gape-unconstrained predation risk. I tested these predictions with common garden experiments in which I measured the foraging, growth, and survival of individual salamander larvae originating from 10 natural populations that varied in gape-limited predation risk. Trait variation among populations was then partitioned into a component attributed to local selection and a component attributed to gene flow from nearby populations exposed to divergent selection.

Results

Common Garden Selection and Phenotypic Assay Experiments.

Mortality was higher for A. maculatum larvae originating from ponds with greater A. opacum predation risk in an experiment in which predators could choose prey from seven different populations under controlled conditions (Fig. 1A; quadratic regression, R² = 0.97; randomization test: P = 0.013). The foraging rates of larvae raised under common garden conditions and exposed to A. opacum cues varied significantly among populations (Fig. 1B; F_9,39 = 3.2; P = 0.005). Foraging rates were higher for larvae originating from ponds with greater A. opacum predation risk (F_1,47 = 16.6; P < 0.001). Substantial variation in population foraging means was explained by A. opacum predation risk in these experiments (quadratic regression, R² = 0.68; F_2,7 = 7.5; P = 0.018). Curvilinear relationships for mortality and foraging rates were suggested by prior simulations (28); linear relationships also were significant and explained substantial variation (R² = 0.70 and R² = 0.60). Foraging rates were positively correlated with mortality in the same populations exposed to A. opacum predation in selection experiments (ρ = 0.86, P = 0.014).

Fig. 1.

Early larval mortality rates, foraging rates, and final weights under common garden conditions in individuals originating from populations with varying gape-limited A. opacum predation risks. (A) The mortality rate of A. maculatum hatchling populations during exposure to free-ranging A. opacum predators in a multipopulation selection experiment. (B and C) Mean foraging rates (B) and final weights (C) under common garden conditions in 10 populations of A. maculatum larvae exposed to different A. opacum predation risks in natal ponds. Foraging rate was measured as the number of feeding attempts that an A. maculatum larva made per minute during the 4 weeks after hatching. Bars represent 1 SEM. Significant (P < 0.05) quadratic relationships are depicted for population-level mortality risk and foraging rate (R² = 0.97 and R² = 0.68, respectively). Linear relationships also were significant.

Consistent differences between populations were evident during the first 4 weeks of the experiment [supporting information (SI) Fig. 3; F_2,46 = 6.1; P = 0.005]. However, a significant linear contrast for the interaction between A. opacum predation risk and early (weeks 1–4) versus late (week 5) foraging (P = 0.023) suggested that A. maculatum foraging rates eventually converged in the fifth week, the period needed by larvae to reach a size refuge in the wild (see Materials and Methods). Other behaviors, including nonforaging movements and proportional time spent in the risky water column, did not differ significantly among populations or in relation to A. opacum predation risk (P > 0.17). In contrast to field observations (see Field Patterns), final larval masses did not differ significantly among populations or in relation to A. opacum predation risk under common garden conditions and standardized food provisioning (Fig. 1C; P > 0.30). This result held even if the population with high growth and zero A. opacum risk was removed from the analysis (P = 0.22).

The heritability of foraging rate varied from 0 to 0.69; three populations had estimates marginally different from zero, which suggests the potential for an evolved response to ongoing selection in these populations (SI Fig. 4). Foraging rate was not significantly related to seven alternative explanations of divergent foraging rates, including the densities of two important gape-limited and gape-unconstrained predators on A. maculatum larvae [Notophthalmus viridescens (red-spotted newt adult) and Dytiscus spp. (diving beetle larva), respectively], total predator densities, total gape-unconstrained predator densities, pond temperature, pond permanence, and conspecific density (SI Table 1; P > 0.12).

Field Patterns.

Under natural conditions where more active foraging could result in greater resource accumulation, elevated growth rates (change in ln head width per day) were observed in ponds with greater A. opacum predation risk (F_1,9 = 3.4; R² = 0.27; P = 0.099) during the first 2 weeks of A. maculatum development. These field growth patterns likely resulted from both differences in genetically determined growth rates and size-specific mortality. Mean early growth rates in these populations were correlated with higher survival in the field (ρ = 0.60; t₉ = 2.2, P = 0.053) during the same period, indicating that rapid growth into a size refuge was associated with higher cumulative survival despite initial declines in survivorship. Growth differences between populations were no longer significant after 4 weeks (P > 0.4).

Spatial Patterns.

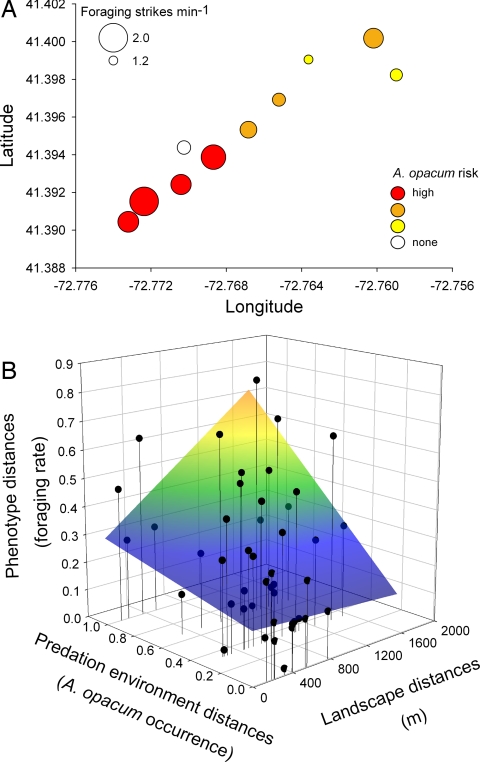
Most ponds with high A. opacum predation risk occurred in the southwest region, whereas most ponds with low risk were found in the northeast region (Fig. 2A). A. opacum predation risk and A. maculatum foraging rate measured in common garden experiments were positively spatially autocorrelated across the region (Mantel test: r = 0.20; P = 0.060; r = 0.31; P = 0.043, respectively). However, population size was not significantly spatially autocorrelated, suggesting that effects were not due to genetic drift in small populations (P > 0.5). In the variance decomposition, both community and spatial variables were related to A. maculatum foraging rate (19.6% and 14.0%, respectively). However, the category that explained the most variation was the interaction between spatial position and local selection (43.8%; overall model: R² = 0.77, F_3,6 = 12.0, P = 0.005), a pattern consistent with a joint influence of local selection and gene flow on trait evolution. I explored this interaction further by examining the relationships among pairwise dissimilarity matrices of genetically determined foraging rates, predation regimes, and landscape distances (Fig. 2B). This analysis showed that populations close together have more similar foraging rates than expected based on local A. opacum predation risk, whereas populations distant from each other and exposed to divergent predator communities exhibited strong trait divergence.

Fig. 2.

Relationships between interpopulation foraging rate, landscape location, and predation risk environment. (A) Map of study populations where symbol size represents mean foraging rate and color indicates A. opacum predation risk (see key). (B) The absolute difference in foraging rates among populations as a function of the pairwise distances between ponds and dissimilarities in predation regimes. The colored surface indicates a least-squares fit to the pairwise distances (R² = 0.27; permutation test: P = 0.031). The shape of the surface suggests that populations have similar genetically determined foraging phenotypes when they share similar predation environments and are located close to one another. Populations have very different phenotypes when they are exposed to strongly contrasting predation risk environments and are far from each other.

Discussion

Community ecologists are tasked with predicting the outcomes of species interactions across heterogeneous landscapes. Besides the multiple ways that environments and communities change across natural landscapes, species interactions also can differ as evolution proceeds in genetically isolated populations (30). Longstanding theory in behavioral ecology predicts that prey individuals should lower their foraging activity to reduce constant predation risk (1, 2, 8). When predation risk varies through time, prey should reduce their foraging during high-risk periods and compensate for lost feeding opportunities during future low-risk periods (e.g., risk allocation hypothesis, ref. 6). However, these theories neglect the potential advantage gained by prey individuals that grow rapidly into a size refuge from gape-limited predation risk (15). Here, I show that intense gape-limited predation risk is associated with the local evolution of risky prey foraging strategies. The observed microgeographic adaptations appear to be mediated by gene flow from divergent local communities. These two pieces of evidence illustrate the need to understand the evolution of species interactions across the regional scales over which gene flow integrates local genetic responses to community heterogeneity.

Growth/Predation Risk Tradeoffs.

A. maculatum responds to reliable cues of A. opacum presence with a generalized plastic response to predation risk that includes preference for low-risk microhabitats and reduced foraging and growth (28). However, given the potential benefits of a size refuge from A. opacum, such highly restricted foraging under predation risk may not be warranted in all communities, especially those dominated by gape-limited A. opacum. Contrary to standard predictions, gape-limited predators can select for prey that grow rapidly into a size refuge (29). Intense foraging is predicted because the potential benefits of rapid growth into a size refuge outweigh the costs associated with elevated initial predation risk. Prey from high gape-limited risk environments still may decrease their foraging compared with no-predator environments, but they should decrease their foraging less than populations exposed only to gape-unconstrained predators. Hence, a size refuge introduces an additional dynamic to risk allocation theories (6) because behavioral decisions affect both instantaneous predation risk and the duration of high-risk predation periods.

In accordance with theoretical predictions, larvae from populations with high A. opacum predation risk foraged more rapidly in the presence of predator cues than those populations with lower risks. Populations that foraged more intensely suffered greater mortality from A. opacum predation at vulnerable hatchling stages. Intense foraging likely decreases larval survival during the first 4 weeks after hatching until a size refuge can be reached. However, it is likely that the long-term fitness benefits of large body size and a size-based refuge from predation eventually outweigh the short-term fitness cost of lower early survival. In contrast, risk-averse foraging behavior may evolve in ponds with low gape-limited predation risk in response to greater relative risks from more homogeneously distributed gape-unconstrained predator species (e.g., Dytiscus). In this way, predator gape-limitation modifies standard predictions generated by theories on growth/predation risk tradeoffs and offers to explain anomalous cases of intense foraging behavior during periods of greatest predation risk. For instance, Fraser and Gilliam (9) found that populations of two fish species from high predation-risk sites tended to forage more frequently under high predation risk. Gape-limited predators cause high mortality in small juveniles in one of these species (31). Together, evidence supports the fine-tuning of growth/predation risk tradeoffs in natural communities to specific predator types defined by their morphological constraints on prey capture over spatial scales that coincide with average migration distances.

Seven alternative and potentially confounding selection agents were tested. None of these was significant. In contrast to other studies (e.g., ref. 32), A. opacum predation risk is relatively uncorrelated with other major axes of environmental variation because A. opacum's distribution is determined largely by winter water temperature, a variable that does not correlate with environmental conditions during the spring–summer development of A. maculatum. Foraging rates were not correlated significantly with the densities of gape-unconstrained Dytiscus larvae or the densities of all gape-unconstrained predators. Prior research suggests that A. maculatum populations do not differ significantly in growth rates in relation to divergent gape-unconstrained predation risks by Dytiscus under similar common garden experiments but with larvae originating from regions where A. opacum is rare or absent (28). Although more active foraging appears to have evolved in response to A. opacum gape-limited predation risk, A. maculatum foraging rates do not covary with Dytiscus gape-unconstrained predation risk. One possible explanation is that A. opacum is more heterogeneously distributed in space and time than Dytiscus (ratio of A. opacum: Dytiscus spatiotemporal coefficients of variation for density: 1.45). As a result, A. opacum's heterogeneous distribution could create a stronger local gradient of antagonistic selection for local adaptation as opposed to a weaker gape-unconstrained gradient that favors generalized adaptations to regional selection (33).

Egg size, an important maternal effect, did not covary with A. opacum risk. Initial hatchling size, which is highly correlated with egg size (ρ = 0.68), was not related significantly to population of origin or A. opacum prevalence in this experiment. These findings, in addition to the demonstration of significant broad-sense heritabilities for several populations, are consistent with the microgeographic differentiation of foraging rate across a gradient in local A. opacum predation risk and the potential for short-term responses to selection across limited distances. However, the co-occurrence of multiple selection agents in wild habitats cautions against strong causal inferences. More definitive tests require field manipulations of natural selection (34).

If the mechanism underlying foraging rate selection can be attributed to growth into a size refuge as suggested by functional ecology, size refuge theory, and observations for the A. opacum–A. maculatum system, then one would expect a correlation between foraging rate and growth rate under controlled conditions. A significant positive correlation was not found here. Three explanations can be offered. First, prey were provisioned with food equally in the experiment, which dampened any effect that increased foraging might have had on growth and led to a nonsignificant correlation between foraging and growth (ρ = 0.03). Foraging rates were positively correlated with growth rates in other experiments performed in more complex habitats, suggesting that foraging and growth rates usually are correlated under more natural conditions (28). Second, the experimental design, involving tightly controlled conditions that facilitated accurate behavioral observations, was artificial; additional factors present in natural environments also affect growth (e.g., spatially heterogeneous resource distributions). Field evidence suggested that A. maculatum larvae in ponds with A. opacum underwent a rapid burst of growth after hatching. Hence, growth under natural conditions was consistent with the variation in foraging rates demonstrated in the common garden experiment. However, field growth was correlated with higher, rather than lower, survival in the field. One possible reason is that the longer time scale over which field survival was measured integrated both the costs (increased mortality) and benefits (reduced mortality) of rapid growth. An overall higher long-term survival rate can be expected if survival increases markedly after growth into a size refuge. A third explanation involves the microevolution of growth–activity relationships under varying predation risk. For example, damselfly species differentially convert assimilated food into growth under predation threat (3). Therefore, the physiological mechanisms that determine mass gain could evolve differently among populations depending on specific predation and resource scenarios, potentially contributing to observed growth differences.

Spatial Location and Trait Variation.

The factor explaining the most variation in inter-population foraging rate was the interaction between a population's spatial position and its local predation risk. In other words, populations located near each other had more similar foraging rates than expected based on pond-specific A. opacum risk. Gene flow offers one reason for landscape trait autocorrelation. This explanation assumes that trait autocorrelation is due to the lack of genetic isolation across short distances and not due to an unknown similarly autocorrelated environmental factor. Although the specific gene flow patterns in the region remain to be determined, I showed that seven key environmental factors were not associated with foraging variation. In addition, I found that effective population size was not significantly spatially autocorrelated, which suggests that observed spatial patterns were not due to differences in population size and the likelihood of genetic drift. I cannot exclude the possibility that historical factors contributed to joint associations between prey foraging and spatial location. However, at this time, observations, theory, and common garden experiments support the working hypothesis that prey foraging rates are under selection by local gape-limited predation risk and modified by gene flow.

Many populations linked by gene flow exist somewhere along a continuum of adaptation and maladaptation, such that the cumulative action of selection on trait variation is determined at the intersection between the scales of local population dynamics and regional migration and gene flow (33, 35). Such maladaptation is important because it can alter the ecological outcomes of species interactions and generate novel genetic variation. Maladaptation can reduce prey survival in populations receiving strong gene flow from an antagonistic predation environment (7, 36). Maladaptation altered the local abundances of competitors and generated higher local species richness in a metacommunity simulation (37). Maladapted prey also can affect predator demography if undefended individuals serve as genetic spatial subsidies to predator populations (26). Last, zones of trait mixing that characterize populations in regions of high selection heterogeneity (e.g., middle of Fig. 2A) can play a central role in maintaining genetic variation and creating novel gene complexes (38).

Conclusions

Ecological applications increasingly require generalizations beyond the population or community scales at which most studies are conducted (39, 40). These endeavors will not succeed unless we can integrate evolutionary and ecological variation at the scale of local populations and at the scale of their regional integration through migration and gene flow. Evidence for genetically determined variation in the magnitude of predator–prey interactions across microgeographic scales demonstrated here and elsewhere (7, 41, 42) implies that predictions from one local community cannot readily be applied to another without additional knowledge about variation in important selection regimes. Results from my study suggest that knowledge about predator-specific constraints on prey capture can be applied to predict the ecological and evolutionary outcomes of predator–prey interactions across natural landscapes. In particular, knowledge about the covariation of size-selective predator densities over spatial or environmental gradients can be used to predict optimal levels of prey foraging. This study also suggests that understanding the spatial mosaic of divergent selection and relative rates of gene flow will be necessary because local maladaptation may be common in natural metapopulations (7, 23, 24). Because variable species interactions have consequences at the level of populations, communities, and ecosystems, understanding the relative contributions of adaptation and gene flow to interaction trait variation will inform ecological predictions across multiple scales.

Materials and Methods

Site Description and Natural History.

I evaluated foraging, growth, and survival rates in A. maculatum prey populations inhabiting 10 temporary ponds situated on an isolated forested ridge (area = 2 km²) on Totoket Mountain near Northford, CT. Ponds differed in the average density of predatory A. opacum larvae. A. opacum adults breed during the autumn in temporary ponds and their larvae overwinter in these ponds. A. maculatum adults migrate into temporary ponds in late March to breed. When A. maculatum salamander larvae hatch from egg masses in late May, A. opacum larvae already have grown to a size (median gape size = 8.2 mm) large enough to prey upon the small (median body width = 2.2 mm) hatchlings. A. maculatum hatchlings cooccurring with A. opacum have low survival in the field (28).

Studies at this site and others demonstrate that A. opacum larvae are strongly gape-limited on A. maculatum larvae (28, 43). In the field, A. opacum larvae consumed prey with an average maximum body width that was 37% (±13% SD) of the predators' maximum gape width (28). In natural selection experiments, A. opacum larvae prey upon A. maculatum larvae with smaller maximum head widths than those available, resulting in a significant positive selection gradient on prey size (28). The average ratio of A. maculatum maximum head width to A. opacum gape width (41% ± 2% SD) generally surpasses A. opacum's estimated mean gape-limitation (37%) by the third week. The observed impact of A. opacum on A. maculatum survival disappears after 3–4 weeks. Therefore, A. maculatum's improved survival after 4 weeks likely occurs because larvae typically outgrow A. opacum's gape limitations over this time period (28).

A. opacum adults breed in most ponds at the study site. However, on average, A. opacum survives the winter in only 63% of the ponds. Consequently, some ponds host A. opacum in high densities reliably year after year, whereas other ponds host A. opacum only once or twice every 3 years depending on winter conditions (also see ref. 43). The long-term probability that A. opacum occurs in a pond likely affects overall breeding success for the iteroparous A. maculatum. Hence, I estimated predation risk as the probability that A. opacum cooccurred with the prey population from 2002 to 2004. This measure of predation risk, A. opacum interannual prevalence, correlates positively with the spring density of A. opacum larvae during this time period (r_S: +0.61, P = 0.037) and A. opacum prevalence in subsequent years (2005–2006; r_S: +0.68, P = 0.014), suggesting that it accurately estimates lifetime predation risk for the prey.

Moderate gene flow likely occurs between closely situated A. maculatum populations. A. maculatum adults move, on average, 114 m and up to 823 m during annual migrations between breeding ponds and terrestrial habitats (literature review, n = 9), indicating the capacity for dispersal into nonnatal ponds (average minimum interpond distance: 92 m). New breeding ponds (e.g., beaver ponds) are quickly colonized (unpublished data). Conversely, adults usually (>70%) return to breed in the same ponds (44). Nearby populations could remain genetically isolated because of this philopatry.

Field Surveys.

I sampled A. maculatum and A. opacum larvae in all ponds in the study region at least every 2 weeks, beginning with hatching and ending when ponds dried or the developmental season ended, from 2002 to 2004. Weekly surveys were performed in 2004 to characterize finer increments of growth and survival differences during early periods of intense A. opacum predation (28). Early larval survival was measured as the exponential decay in larval density for each of the first 3 weeks after hatching using this fine-scale survey data. Growth was measured as the change in ln(larval head width) per day during the same time periods.

Prey Selection Experiment.

Here, I examined whether predator-induced mortality covaried with observed genetic differences in foraging rate among populations. For this experiment, 10 eggs were separated with a scalpel from each of three egg masses collected within 3 days of being laid in seven ponds in spring 2003. Each egg cluster was raised to hatching in an incubator (Precision model 818, Winchester, VA) under controlled temperature and light conditions (14.0°C; 12:30/11:30 light/dark cycle consistent with natural temperatures and day length) in six-well culture plates until hatching. Each hatchling was photographed with a digital camera attached to a 7× microscope. Hatchlings were randomly distributed among six separate selection arenas, such that 17 hatchlings from multiple natural populations were exposed to one wild A. opacum predator in each selection trial. Each predator gape was within 1 SD of the mean gape size observed in the field when A. maculatum hatch. Selection was conducted in 60-liter wading pools filled with aged, treated water, 25 randomly selected deciduous leaves for natural substrate, and a standardized aliquot of field-collected zooplankton as prey food resources. Selection arenas were placed outdoors under 50% shadecloth to mimic natural forest canopy. After 5 days, all surviving larvae were recovered and rephotographed. Recovered larvae were assigned to population of origin by matching pre- and postselection photographs of spotting patterns. Because selection occurred within independent arenas, I evaluated the significance of the relationship between mean mortality rate per day [measured as −ln(survival)/time] per population and A. opacum predation risk by comparing the observed regression coefficient versus the distribution of coefficients returned by permuting data within arenas 10,000 times.

Common Garden Phenotypic Assays.

The common garden study design incorporated five full-siblings from each of five families from each of 10 ponds with the exception of one pond (Ordway) for a total of 245 replicates. Only four egg masses were collected from Ordway before it dried prematurely. Egg masses were collected in the field within 2 days of egg-laying in spring 2004. To facilitate hatching, egg clusters were placed in 10 cm (mean submersion of eggs in field) of aged treated water in individual 19-liter containers randomized in an outdoor enclosure. After hatching, five larvae were selected arbitrarily from each family. Each larva was placed in a separate 1-liter clear plastic culture container and assigned randomly to a location in a temperature-controlled room. Containers were moved every 2 days to minimize effects of incubator location. Temperature was set to 14.3°C (±0.5°C SD) to match mean natural pond temperatures. Light/dark cycles reflected natural day length for the region. Every 2 days, I added equal aliquots of 25 ml of water conditioned by A. opacum that had been fed A. maculatum larvae in 68-liter bins and filtered through 70-μm Nitex mesh. Similar concentrations of A. opacum cues induced behavioral reactions in prior research (28). Equal numbers of size-matched (using nested subsets of mesh filters) cultured Daphnia magna were added to each container every 2 days. I increased the number and maximum size of Daphnia over time according to A. maculatum size and appetite. The small container size, the need to standardize D. magna additions, and voracious appetites prevented me from provisioning food ad libitum. Instead, I added equal food resources to each container.

Each week, behavioral surveys were conducted during the day (0900–1300) and night (2100-0100). Nighttime surveys were performed using a dim red-filtered light source previously shown to have no effect on larval behavior (28). I recorded foraging attempts, nonforaging movements, and position (bottom or water column) for each container consecutively in a block 10 times per survey for a total of three to six surveys per time period. A foraging attempt was defined as a rapid forward movement accompanied by mouth suction. I recorded mean foraging rate as feeding attempts divided by total observation time for four day/night survey periods (the period of natural vulnerability to A. opacum) for a total of 320 observations per individual. The experiment was ended after 5 weeks, just past the normal duration of natural A. opacum predation risk. The additional behavioral survey in the fifth week allowed me to compare behaviors before and after the period of natural A. opacum vulnerability. Only one larva died during the experiment (survival = 99.6%).

Initial size was evaluated from the centroid of 18 landmarks digitized from side and dorsal photographs of each larva. This nonintrusive procedure provides size estimates that are highly correlated with mass (ρ = 0.87). One potentially important maternal effect, initial hatchling size, did not differ significantly among ponds or in relation to A. opacum predation risk in this experiment (P > 0.48). At the end of the experiment, each larva was wet-weighed on a Mettler (Columbus, OH) AE-100 electronic scale (±0.1 mg). Final larval mass was used as a measure of growth rate. Results were unaltered if the change in morphological centroid size over time was used instead. After ln(x + 1) transformation, foraging, movement rates, and size met the normality assumptions required for parametric analyses [K² test (45)]. The arcsine transformation was applied to the proportion of time spent in the water column for the same reason.

Several alternative hypotheses were explored to see whether other potentially correlated selection regimes might explain foraging rate. These selection regimes included mean field densities over 3 years of two common predators of A. maculatum larvae in the region: (i) the gape-limited N. viridescens and (ii) the Dytiscus spp., which is considered to be a gape-unconstrained predator of A. maculatum larvae because Dytiscus can prey upon even the largest A. maculatum larva. I also evaluated the effect of total predator density and total gape-unconstrained predator density. A significant effect of natal temperature regime on foraging rate could signal locally adapted temperature-dependent growth (46). Therefore, I also analyzed foraging rate versus the mean spring pond temperature for the 5 weeks after hatching (the common garden experiment's duration). Last, I assessed the potential contribution of intraspecific densities, and possible competitive effects, to variation in foraging rate.

Analyses were performed in S-Plus v. 7.0 (Insightful, Seattle, WA). Foraging and growth rates were evaluated in a mixed analysis of variance (ANOVA) or covariance (ANCOVA) with either pond or A. opacum predation risk in the natal pond as fixed effects and family as a random effect (47). Foraging through time was evaluated in a mixed ANCOVA with ponds assigned to one of three categories: constant, variable, or no A. opacum risk. Each individual was nested within clutch as a random effect to account for repeated measures. Broad-sense heritabilities were estimated by using standard techniques for full-sibling designs in a series of one-way ANOVAs. Permutation tests (n = 10,000) were used to assess significance (48). Because heritabilities estimated in this way include the potential contributions of dominance, epistatic, and maternal variances, they should be interpreted as an upper limit to narrow-sense heritability.

Spatial Patterns.

To examine whether landscape position affected population differentiation, I partitioned the variation in interpopulation foraging rate between descriptors of local selection (A. opacum risk) and spatial location (latitude and longitude). Pond location was described by a linear trend-surface analysis (49). Centered and standardized pond coordinates and their interaction were entered into a regression model. This trend surface was reduced to a more parsimonious model of longitude based on the Akaike information criterion. The foraging variation attributed to spatial position and from A. opacum predation was partitioned by using standard methods (49). To visualize the interaction between spatial location and predation risk revealed by this statistical model, I estimated the response surface of pairwise absolute interpopulation foraging rate differences versus pairwise Euclidean distances among ponds and pairwise absolute differences among predation environments. Surface fit was evaluated by a permutation of the raw data (n = 10,000). Mantel tests were used to evaluate spatial autocorrelation in A. opacum predation risk, prey foraging rate, and effective population size (n = 10,000). I estimated effective population size as the harmonic mean of three annual estimates of egg mass censuses divided by 2 (mean egg masses per female).