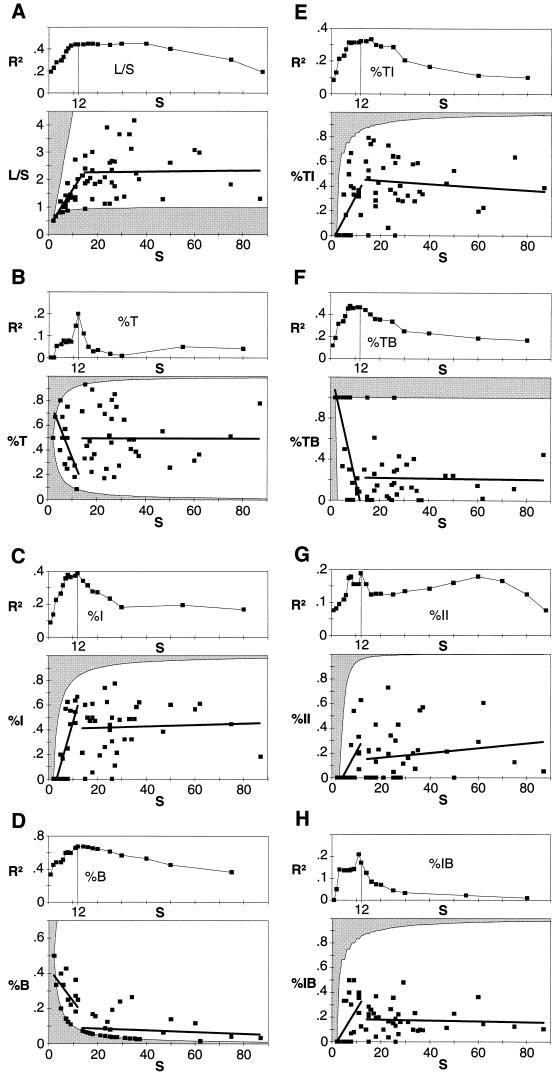
Figure 3.

Data and discontinuous linear piecewise regression models of the food web properties for the 60 original food webs of Sugihara et al. (5). For each property, the first plot gives the value of the coefficient of determination, R², for different positions of the breakpoints (the constant c in Eq. 1). The second plot presents the data and the regression lines for a breakpoint at S = 12 (S is the number of species). The upper and lower limits of the properties, given that there are no loops of the kind where species A eats species A or species A eats species B and species B eats species A are indicated by the shaded region. The properties, the coefficients of the piecewise linear regressions (from Eq. 1), and the results of t tests for the slopes b₀ and b₁ are as follows. (A) link density, L/S: a₀ = 0.211, b₀ = 0.140 (t = 6.49, P < 0.0001), a₁ = 2.216, b₁ = 0.0015 (t = 0.180, P = 0.858); (B) fraction of top species, %T: a₀ = 0.785, b₀ = −0.048 (t = −4.75, P = 0.0001), a₁ = 0.496, b₁ = 0 (t = −0.004, P = 0.996); (C) fraction of intermediate species, %I: a₀ = −0.216, b₀ = 0.067 (t = 5.35, P < 0.0001), a₁ = 0.408, b₁ = 0.0005 (t = 0.267, P = 0.791); (D) fraction of basal species, %B: a₀ = 0.430, b₀ = −0.019 (t = −2.69, P = 0.0134), a₁ = 0.096, b₁ = −0.0005 (t = −0.865, P = 0.393); (E) fraction of links between top and intermediate species, %TI: a₀ = −0.064, b₀ = 0.038 (t = 2.92, P = 0.0080), a₁ = 0.474, b₁ = −0.0013 (t = −0.635, P = 0.530); (F) fraction of links between top and basal species, %TB: a₀ = 1.285, b₀ = −0.107 (t = −4.79, P < 0.0001), a₁ = 0.218, b₁ = −0.0002 (t = −0.088, P = 0.931); (G) fraction of links between intermediate and intermediate species, %II: a₀ = −0.167, b₀ = 0.037 (t = 3.73, P = 0.0012), a₁ = 0.121, b₁ = 0.0019 (t = 0.956, P = 0.346); (H) fraction of links between intermediate and basal species, %IB: a₀ = 0.055, b₀ = 0.032 (t = 2.76, P = 0.0115), a₁ = 0.186, b₁ = −0.0004 (t = −0.351, P = 0.728).