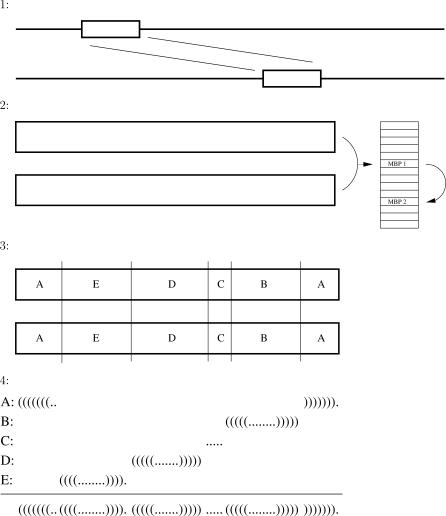
Figure 3. The Divide and Conquer Algorithm.

(1) In the first step, the region of interest is found using the local-alignment algorithm. During the local alignment, the bifurcation constraint is used to save a lot of memory.

(2) In the second step (first step of a global alignment), the region of interest is realigned. The bifurcation constraint is still used, but an additional list of branch points is made. The list stores the six coordinates of the branch point and pointers to the next branch points (one for each of the two substructures). For each subalignment, a pointer to the last branch point is kept.

(3) Using the branch point pointers and coordinates, the alignment is split into shorter unbranched segments. Here A is an initial unbranched segment. MBP 1 (Multi Branch Point) splits the alignment into two segments: EDC and B. C is a new initial unbranched segment. MBP 2 splits the ED segment into the E and D segments.

(4) The five segments are realigned and backtrack without using the bifurcation constraint to save memory. These realignments are fast, as it is not necessary to evaluate the bifurcation part of the algorithm. Finally, the segments are joined together into the final alignment.