Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2007 Aug 17;35(16):5593–5609. doi: 10.1093/nar/gkm598

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© 2007 The Author(s)

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/2.0/uk/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

PMC Copyright notice

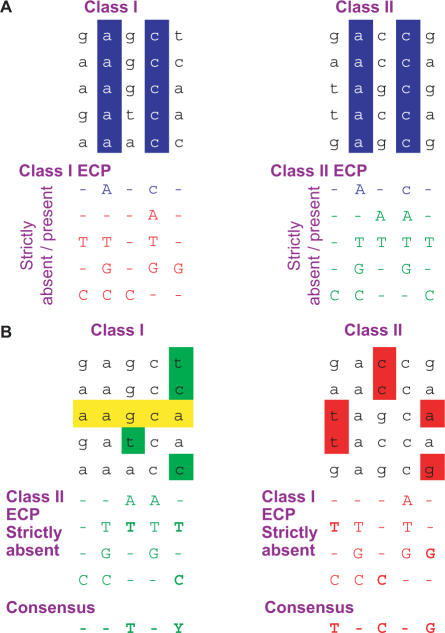
Figure 1. — The principle of the extended consensus partition (ECP) algorithm. The principle of the ECP algorithm is illustrated on samples of short nucleotide sequences which may belong to two artificial Classes I and II. (A) Construction of the class-specific ECP sets. As shown in (A), sequences that belong to a presumed class are aligned and each position is evaluated for (i) the existence of a strictly present nucleotide type and (ii) the strict absence of one or more nucleotide types. The list of these two disjoint subsets of strictly present (colored in blue) and strictly absent (colored red for Class I and green for Class II) nucleotides at each position constitutes the ECP of a given class of sequences. (B) Using the class-specific ECP set to filter sequences from the opposite class. Once the class-specific ECP is generated, it can serve as a filter that separates any new sequences (in this case coming from the opposite class) into two groups. One group will contain sequences that can belong to the given class, while the other contains those that are excluded. The filtering works such that a sequence should belong to the class if the following two simple criteria are fulfilled: (i) the strictly present elements of the ECP should be present in the sequence and (ii) the sequence should not contain any residues strictly absent from the given class. This can be illustrated as shown in (B) as intersections. The rules from Class I are shown underneath Class II sequences and vice versa. The intersection of the sequence elements with the ‘opposite’ class rules are highlighted both in the sequences (as colored background) as well as in the rule set (as bold). The consensus of such bold nucleotides for each position is shown in the bottom row in A and B using the IUPAC code: A, C, G, T, R (A or G), Y (C or T), M (A or C), K (G or T), B (C, G or T), D (A, G or T), H (A, C or T), V (A, C or G) or N (A, C, G or T). It constitutes the discriminating subset of the ECP, or as we call the ‘discriminating class-specific elements’. These elements are listed for the 50 analyzed species in Figure 4. When a sequence has intersection with the strictly absent ECP set of the opposite class, it is excluded from that class. When a sequence (highlighted with yellow) has no intersection with the strictly absent ECP of the opposite class ECP, it could be classified into both classes. We call this sequence as false positive in the class it should not belong to.