TABLE 1.

Summary of results of testing done on simulated data

Simulated parameters	Deviation from model	Median	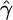Median	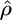Median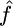
γ = 0, ρ = 1 (f = 0)	None	0.5332 (11.5)	0.9706 (96.9)	0.55 (11.5)
	Growth	0.5863 (16)	0.9045 (89)	0.586 (16)
	Bottleneck	0.4777 (18)	0.8678 (95)	0.516 (18)
	Structure	0.5472 (5)	0.9415 (97)	0.634 (5)
	Selection	0.6031 (8)	0.9464 (98)	0.667 (8)
γ = 1, ρ = 1 (f = 1)	None	1.348 (77.3)	0.9323 (95.8)	1.45 (62.9)
	Growth	1.344 (71)	0.8907 (94)	1.36 (55)
	Bottleneck	1.286 (75)	0.8868 (97)	1.43 (64)
	Structure	1.401 (84)	0.9077 (98)	1.48 (67)
γ = 10, ρ = 1 (f = 10)	None	9.428 (99.9)	0.9708 (94.0)	9.54 (90.1)
	Growth	7.805 (97)	0.8738 (92)	9.08 (87)
	Bottleneck	8.315 (97)	0.8997 (94)	8.91 (82)
	Structure	8.455 (99)	0.8927 (93)	9.50 (89)
	Genotype	7.49 (97)	1.21 (93)	6.24 (68)

We first simulated data sets according to standard model assumptions (constant sized, panmictic population with neutral evolution), with θ = 1, and a variety of values of f. For each set of parameters 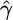, , 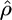and 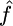, the median estimate for 1000 independent simulations is given, with the proportion of data sets for which the estimate lies within the range (truth/2, truth × 2) in parentheses. In the case f = 0, we see that in 11.5% of cases we found 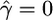. However, for 82.8% of these data sets, 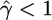/kb. We also show the corresponding results for 100 data sets simulated with a range of deviations from the above assumptions (see text). These results are broadly similar to those with no deviation, except in the case of rephased data where the crossover rate is overestimated.