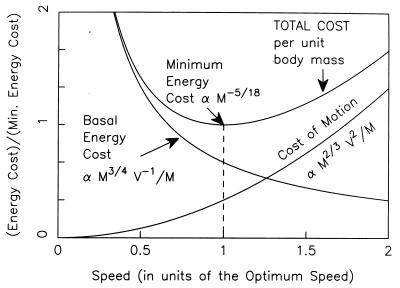
Figure 9.

The energy cost of transport over unit distance versus speed for swimming fishes. For transport of mass M over unit distance at uniform speed V, the basal cost is A/V and that for motion is BV², where A is assumed proportional to M^3/4 (metabolic rate), and B proportional to M^2/3 (surface area for self-similar shapes) and includes conversion efficiencies. Then, for unit body mass, the minimum energy cost is proportional to M^−5/18 (the slope in Tucker’s plot) and is achieved at an optimum speed, which, for the above assumptions, is effectively independent of the mass, actually proportional to M^1/36. (It would be truly independent of the mass if the dependences of A and B on mass had a common exponent, say γ. The minimum energy cost then would be proportional to M^(γ−1).)