Computing the distribution of the maximum in balls-and-boxes problems with application to clusters of disease cases

Abstract

We present a rapid method for the exact calculation of the cumulative distribution function of the maximum of multinomially distributed random variables. The method runs in time O(mn), where m is the desired maximum and n is the number of variables. We apply the method to the analysis of two situations in which an apparent clustering of cases of a disease in some locality has raised epidemiological concerns, and these concerns have been discussed in the recent literature. We conclude that one of these clusters may be explained on purely random grounds, namely the leukemia cluster in Niles, IL, in 1956–1960; whereas the other, a leukemia cluster in Fallon, NV, in 1999–2001, may not.

It happens from time to time that cases of a disease will cluster both geographically and in time in a manner that seems not to be random and that invites further epidemiological study.

Of course, mathematics alone cannot answer serious questions of public health, but it can provide guidelines about what sort of clustering should be regarded as unusual and what sort is to be expected. In particular, the calculation of a P value is required for an objective assessment of any observed event. In this paper we provide a rapid and exact P value calculation for the standard “balls-in-boxes” model appropriate to a disease-clustering situation.

The Model

Suppose that during a certain time period, a number r of cases of some disease arise randomly in some large population, such as that of the United States. Let N be the size of that population and N₀ be the population of the community in which the seemingly large number of cases has occurred.

We think of the entire country as consisting of n = N/N₀ identical communities, or cells, each containing N₀ people, and we ask

If r cases occur randomly in the populations of n communities of the same size, what is the probability that no community gets more than m cases of the disease?

The standard calculation required to answer this question involves the “balls-in-boxes” model, discussed below. If, for example, it turns out that it is extremely likely that some community of equivalent size to that in which the seemingly large number of cases occurred would have that many cases purely by chance, we could conclude that the observed cluster would not be a cause for further suspicion of communicability of the disease or the existence of environmental causative factors. Likewise, if it turns out that it is extremely unlikely that, by chance, any community of that size would have the observed number of cases of the disease, then support would be given to the possibility of a public health hazard.

The Mathematics

Mathematically speaking, we have r “balls” (the disease cases) being dropped randomly into n labeled “boxes” (the communities). The relevant calculation thus concerns the P value associated with the box (or boxes) having the largest number of balls in it. It is well known that the distribution function of the maximum of a number of random variables changes sharply near the mean of the maximum, so that an exact rather than an approximate calculation is needed to find this P value. We provide this exact calculation in this paper.

The P value associated with an observed value m of cases of the disease in the community of interest is the probability that the maximum number of balls in any box is m or more. We find this probability by first finding the probability that no box contains more than m balls. Denote this probability by P(r, n, m).

Now, the probability that there are r₁ balls in box 1, and r₂ in box 2, and …, and r_n in box n, is given by the well known multinomial distribution,

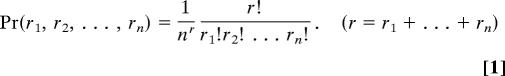The probability that no box contains more than m balls (i.e., the cumulative distribution function of the maximum of the r_i, evaluated at m) is

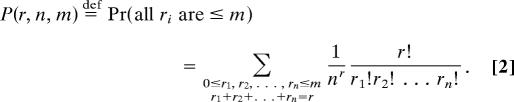The Computation

At first sight, the expression of Eq. 2 seems appallingly complicated for exact computation, if r and n are large. Various approximations, such as the Poisson approximation, have been used by researchers to avoid the apparently tedious computation in Eq. 2.

However the exact calculation can be completely tamed by two steps. First, we introduce the function

which is simply the mth section of the exponential series. Then P(r, n, m) is r!/n^r times the coefficient of x^r in the series e_m(x)ⁿ. (See Appendix 1 below for a derivation.) The question of computing a particular coefficient of a high power of a given power series is a well studied problem in computer science, and the following solution, which makes the computation quite rapid and easy to program, is taken from ref. 1, chapter 21.

Let f(x) = Σ_j a_jx^j be a given power series and let h(x) = f(x)ⁿ. The question is, If h(x) = Σ_j h_jx^j, how can we economically compute the h_j values from the given a_j values? We begin by taking logarithms of the equation h = fⁿ, to get log h(x) = n log f(x). Now differentiate both sides with respect to x to obtain h′/h = nf′/f, and cross-multiply to eliminate fractions, yielding fh′ = nhf′. Next, insert the power series expansions of the various functions into this equation and multiply both sides by x, for cosmetic reasons, to get

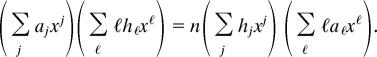Finally, equate the coefficients of a given power of x, say x^s, on both sides of the last equation, which gives,

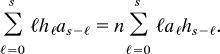This is a recurrence relation. We can use it to compute the unknown h_j values successively, in the order h₀, h₁, h₂, …. To make this explicit, we can rewrite the above in the form

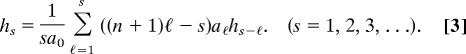In this form it is clear that each h_s is determined from h₀, h₁, …, h_s−1.

In the particular case at hand, of powers of the truncated exponential series e_m(x), we have a_j = 1/j!, for 0 ≤ j ≤ m, and a_j = 0 for all other values of j. The recurrence takes the form

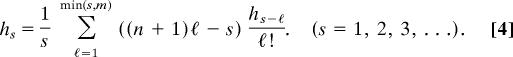We summarize the calculation procedure as follows. To compute P(r, n, m) as defined by Eq. 2,

• Take h₀ = 1 and successively compute h₁, h₂, …, h_r from Eq. 4.

• Then P(r, n, m) = r!h_r/n^r.

A remarkable feature of this algorithm is that the computation of each h_s requires the knowledge of only m earlier values, so the entire computation can be done with just m units of array storage. For example, it can find the probability that the maximum is ≤8, for 15,000 balls in 10,000 boxes by using only 8 array storage locations. In summary, it runs in a time that is O(mn) and uses only O(m) storage.

We remark that, as we have presented it, this method works only for the situation in which the cells have equal probabilities. It can be extended, with some extra cost, to the case of unequal probabilities, which may be useful for power calculations.

Leukemia: Two Examples

Example 1.

We consider first the much discussed case (see refs. 2 and 3) of childhood leukemia in Niles, IL, in the 5-year period 1956–1960. Heath (3) gives a total of eight cases in this town during this period, as compared with an expected number of 1.6. In 1960, the population of Niles was ≈20,000 people. The total population of the U.S. in 1960 was ≈180,000,000 people. Therefore the U.S. population in 1960 can be thought of as consisting of 9,000 cells, the population of each being 20,000 people. An expected number of 1.6 in Niles would then correspond to a total of ≈14,400 cases in the U.S. in the 5-year period studied.

Using the formula above, we therefore computed the exact probability that if 14,400 balls are distributed randomly into 9,000 cells, then no cell will get more than m balls, for each m = 6, …, 12, and in particular for m = 8. We also computed the P value for each of these values of m by using the fact that the P values corresponding to an observed maximum of m is given by 1 − P(14400, 9000, m − 1).

For comparison, we ran a Monte Carlo computer experiment in which we repeated 1,000 times the operation of distributing 14,400 balls randomly into 9,000 cells and recorded the frequencies of the maximum occupancy numbers, thus giving an empirical distribution function for m (1,000 replications are needed to give an estimate of the P value for m = 8 that is accurate to within ±0.01 with probability 0.95). The results of this simulation, and the exact P(14400, 9000, m) computations are shown in Table 1, together with the exact P values.

Table 1.

The Niles, IL, computation

m	P(14400, 9000, m)	Monte Carlo	P value
6	0.000005	0.000	1.000000
7	0.095395	0.096	0.999995
8	0.664954	0.678	0.904605
9	0.937864	0.944	0.335046
10	0.990843	0.993	0.062136
11	0.998788	0.998	0.009157
12	0.999852	0.999	0.001212

The computation of the exact values required <5 sec on a personal computer running algebra system Maple (available from the authors upon request). The Monte Carlo computations required ≈30 min. In both the Monte Carlo simulations and the exact calculations, we observed the expected rapid change of P values as m increases, emphasizing the need for exact P value calculations as disscussed in the text.

We conclude from the results in Table 1 that the probability that some cell with a population of 20,000 would have gotten eight or more cases in the 5-year period studied is ≈90%. Thus, the Niles data do not appear, so far as formal P value calculations are concerned, to show a significant cluster of cases of childhood leukemia.

Example 2.

Twelve cases of acute lymphocytic leukemia were observed (4) in Churchill County, NV, among persons who had been residents of the county at the time of diagnosis, in the 3-year period 1999–2001. Concern was expressed that this cluster was due to exposure to some agent associated with a nearby naval air station. At that time the county had a population of ≈24,000. The entire U.S. had a population of ≈288,000,000, equivalent to 12,000 units, or cells, each of the size of Churchill County. The Nevada State Epidemiologist, Randall Todd, estimated that, based on its population, about one case would be expected in Churchill County every 5 years. If we use that estimate, the incidence in the U.S. as a whole would be 12,000 cases every 5 years, or 8,000 cases per 3-year period.

In this case, we need the distribution function of the maximum number of balls in any cell if 8,000 balls are thrown at random into 12,000 cells. The results are shown in Table 2.

Table 2.

The Fallon, NV, computation

m	P(8000, 12000, m)	P value
4	0.000472	1.000000
5	0.436361	0.999528
6	0.925122	0.563639
7	0.993604	0.074878
8	0.999528	0.006396

Clearly the observed incidence of 12 cases in Churchill County cannot reasonably be ascribed to chance, and further epidemiological investigation is warranted.

Further Comments on the P Value

The P value corresponding to any value of m in the balls-in-boxes case can in principle be calculated exactly by using standard inclusion/exclusion formulae. In practice, this seems extremely difficult, because the alternating signs can cause catastrophic loss of significant digits. A Poisson approximation is also possible but may be inaccurate, particularly around the tails of the distribution. Our exact method, described in Eq. 4, is fast and does not suffer from any of those problems.

A further comment about P values is more wide-ranging. Many diseases might come to our attention because of an apparent clustering in some location in some time period. In addition, many different time periods might be potentially observed. An overall P value calculation taking these matters into consideration would be desirable but in practice would probably be impossibly difficult, since no precise value can be attached to “the number of diseases that might come to our attention” or, possibly, to the number of time periods that we might have considered.

A Disclaimer

Mathematics cannot prove or disprove the communicability or environmental origins of a disease process. It can only help to define the word “unusual.” The benchmark given above seems like an appropriate one to use when investigating an outbreak that is localized spatially, temporally, or both. By this benchmark, the clustering of leukemia cases in Niles, IL, between 1956 and 1960 was not unusual. In fact, some collection of that number of cases in some community the size of Niles in a 5-year period of keeping records was to be expected with high probability. On the other hand, the Churchill County data seem extremely significant.

Some Related Work

The problem of finding the distribution of the maximum occupancy in a balls-and-cells problem is very old. Already in the work of Barton and David (5) one finds the first of our two observations, namely that the desired probability is a certain coefficient in a power of a given power series. In ref. 6, this observation of Barton and David is cited and is said to be “not in a form convenient for computing,” which is true absent our second step (in Eq. 3) of vastly accelerating the computation of the high power of the given series.

Freeman's algorithm in ref. 6 sought to economize the computation by grouping together vectors of occupancy numbers that, as unordered multisets, were the same. Hence, he listed partitions with given largest size part and counted the occupancies of that subset of all partitions. This approach requires considerably more labor than our method above.

Likewise the recurrence (Eq. 3) for computing powers of power series has a long history. Although we have followed ref. 1 in our presentation, the recurrence method was certainly not invented by the authors of ref. 1, because this method is described in several earlier works. Nonetheless, the concatenation of the two methods in connection with finding the distribution of the maximum cell occupancy seems to be new.

Finally, we mention some very recent work (7, 8) on a different problem but one that presents a similar challenge. This problem is the normalized maximum likelihood distribution, which arises in connection with finding the shortest possible encoding of a given data set. The problem concerns the rapid computation of

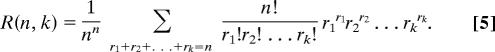This formula, aside from the multiplicative factor, is evidently the coefficient of xⁿ in B(x)^k, where B(x) = Σ_n nⁿxⁿ/n!. Our algorithm (Eq. 3) clearly applies here. In ref. 8, the authors discovered that the elegant recurrence

holds, owing to special properties of the function B(x), and this yields an algorithm that runs in time O(n + k), which is faster than our general algorithm (Eq. 3) when specialized to this case. However, if, for a fixed k, we want a table of R(n, k) for all n = 1, 2, …, N, then our algorithm (Eq. 3) will compute all N of those numbers at an average cost of O(N) computations per number computed, which is about the same as the method of ref. 8.

Appendix 1: Powers of a Power Series

Suppose we have a power series f = Σ_r a_rx^r. Then, when we raise the series f to the nth power, we obtain

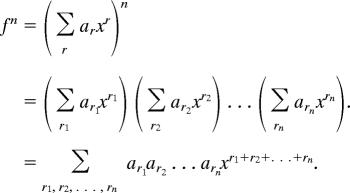The coefficient of x^r in the above is evidently obtained by requiring that r₁ + r₂ + … + r_n = r, and therefore it is

Next we specialize this expression to the case for which the f series is the mth section of the exponential series. This means that we are taking a_j = 1/j!, for j ≤ m, and a_j = 0 otherwise. The general expression (Eq. 6) then becomes exactly the cumulative multinomial probability (Eq. 2), aside from the factor r!/n^r, as claimed. For more information about power series generating functions, see, for example, ref. 9.