Phylogenetic incongruence in the Drosophila melanogaster species group

Abstract

Drosophila melanogaster and its close relatives are used extensively in comparative biology. Despite the importance of phylogenetic information for such studies, relationships between some melanogaster species group members are unclear due to conflicting phylogenetic signals at different loci. In this study, we use twelve nuclear loci (eleven coding and one non-coding) to assess the degree of phylogenetic incongruence in this model system. We focus on two nodes: (1) The node joining the D. erecta-D. orena, D. melanogaster-D. simulans, and D. yakuba-D. teissieri lineages, and (2) The node joining the lineages leading to the melanogaster, takahashii, and eugracilis subgroups. We find limited evidence for incongruence at the first node; our data, as well as those of several previous studies, strongly support monophyly of a clade consisting of D. erecta-D. orena and D. yakuba-D. teissieri. By contrast, using likelihood based tests of congruence, we find robust evidence for topological incongruence at the second node. Different loci support different relationships among the melanogaster, takahashii and eugracilis subgroups, and the observed incongruence is not easily attributable to homoplasy, non-equilibrium base composition, or positive selection on a subset of loci. We argue that lineage sorting in the common ancestor of these three subgroups is the most plausible explanation for our observations. Such lineage sorting may lead to biased estimation of tree topology and evolutionary rates, and may confound inferences of positive selection.

Drosophila melanogaster and its relatives have been used extensively in studies of genetic and morphological variation within and between species. For example, inferences concerning the relative roles of drift, purifying selection, and positive selection in shaping patterns of genetic variation in D. melanogaster often benefit from comparisons to the closely related species D. simulans and D. yakuba (e.g., McDonald and Kreitman, 1991). Similarly, comparative morphologists have used D. melanogaster and its relatives to study the evolution of a number of traits, e.g., genital morphology (Kopp and True, 2002a) and pigmentation (Wittkopp et al., 2002; Prud’homme et al., 2006).

Opportunities for, and interest in, using the genus Drosophila in comparative biology is likely to grow in the near future. The availability of complete genome sequences for twelve members of the genus Drosophila (http://species.flybase.net), as well as for several other dipterans, promises to facilitate genome scale studies of molecular evolution. These comparative data will allow for the detection of functionally important genomic regions, as indicated by high levels of conservation or by the signature of positive, diversifying selection. Moreover, the application of genetic and transgenic techniques developed in D. melanogaster to other species will facilitate studies of evolution and development.

Different levels of taxonomic organization have proven useful for comparisons of different traits of interest. Rapidly evolving characters, such as genital morphology, necessitate the use of closely related taxa (e.g., Kopp and True, 2002a). Over longer taxonomic distances, it may become difficult to distinguish the ancestral from the derived state, because all extant taxa will be highly derived. Moreover, the likelihood of observing homoplasies (independent mutational events leading to a shared character state) increases with greater evolutionary time. The study of slowly evolving characters, by contrast, requires the use of more distantly related species, such that sufficient time has elapsed in order to observe evolutionary change.

With respect to D. melanogaster, we expect that comparisons within the melanogaster subgroup and group will be particularly relevant to many comparative studies (Fig. 1), particularly in comparative genomics. With greater phylogenetic distance, synonymous sites become saturated, undermining the utility of dN/dS based measures of molecular evolution. In comparisons between the fully sequenced genomes of D. melanogaster and D. pseudoobscura, for example, enough synonymous sites have sustained multiple hits to substantially reduce the power and reliability of the dN/dS ratio (Richards et al., 2005). The so-called “oriental” subgroups (takahashii, eugracilis, elegans, suzukii, ficusphila, rhopaloa), which are thought to be intermediate in divergence between D. melanogaster and D. pseudoobscura (Lemeunier et al., 1986), may therefore be of particular use, since synonymous sites are typically not saturated (e.g., Swanson et al., 2004; Malik and Henikoff, 2005). Moreover, the species comprising the oriental subgroups display an impressive array of morphological diversity (e.g., Kopp and True, 2002a; Prud’homme et al., 2006).

Figure 1.

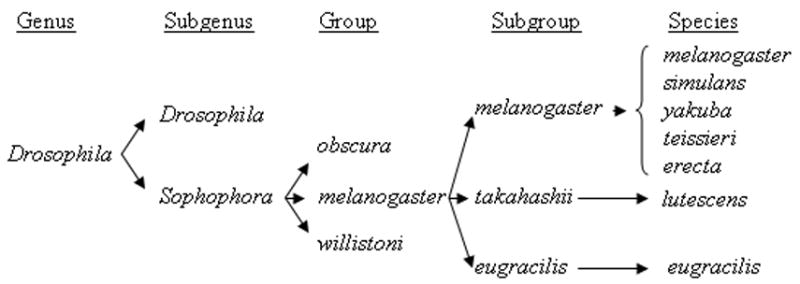
Taxonomic subdivisions in the genus Drosophila. Only species and subgroups represented in this study are listed; other groups and subgenuses are indicated for illustrative purposes only.

Most statistical methods used in comparative genomics and comparative morphology require explicit use of a phylogeny of the taxa under consideration. For example, PAML, a software package used frequently for detecting positive selection at the codon level, requires specification of a tree or trees upon which evolutionary parameters are estimated (Yang et al., 2000). Phylogenetic considerations are crucial; for example, it is only through use of a phylogeny that one can distinguish between shared genealogy and convergent evolution as explanations for a shared character state. A robust phylogeny of the Drosophila melanogaster species group will therefore prove important for future comparative work.

Despite numerous attempts to infer phylogenies within the Drosophila melanogaster species group, several relationships have proven difficult to resolve. Within the melanogaster subgroup, three pairs of sibling species (or species complexes) are well established: melanogaster/simulans (and associated simulans complex species), erecta/orena, and teissieri/yakuba (and D. santomea). It is thought that the three species complexes of the melanogaster subgroup diverged between 6 and 15 million years ago (Lachaise et al., 1988). The relationships among these species pairs have proven controversial (Fig. 2), although recent molecular studies appear to converge on a single topology (Ko et al., 2003; Kopp and True, 2002b). LaChaise et al. (1988), on the basis of biogeographic considerations, places the erecta/orena clade basal within the subgroup (this configuration is denoted Topology I by Ko et al. 2003, whose nomenclature we follow here). Jeffs et al. (1994) and Russo et al. (1995) support this hypothesis using nuclear gene sequence data. Several other studies find evidence for a closer relationship between the teissieri/yakuba and erecta/orena species pairs (Topology II; Arhontaki et al., 2002; Gailey et al., 2000; Ko et al., 2003). Finally, one study places D. erecta and D. orena closest to the melanogaster/simulans complex (Topology III; Schlotterer et al., 1994).

Figure 2.

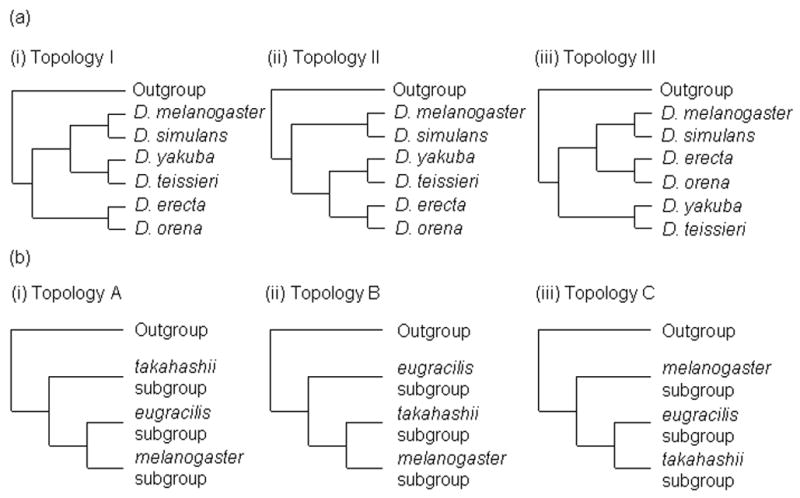
(a): Possible tree topologies of the melanogaster subgroup (b): Possible tree topologies of the melanogaster species group.

Relationships between the melanogaster subgroup and the oriental subgroups have also been difficult to resolve (Fig. 2). Here, we focus on the branching orders of the eugracilis, takahashii, and melanogaster subgroups, which likely diverged between 15 and 30 million years ago (Lachaise et al., 1988). Analyses of several nuclear genes place the takahashii subgroup basal within the species group, with strong bootstrap support (we will call this Topology A; Ko et al., 2003). Other studies, with similarly strong support, find a basal position for the eugracilis subgroup (Topology B; Kopp and True, 2002b; Yang et al., 2004). A third topology, according to which the eugracilis and takahashii subgroups are more closely related to each other than either is to the melanogaster subgroup (Topology C), is supported by mtDNA (Kastanis et al., 2003).

Although previous studies have used multiple loci to infer different phylogenies within the melanogaster species group and subgroup, none has explicitly addressed the issue of incongruence between loci. It is unclear whether apparent disagreements between loci are statistically robust, and the underlying causes of incongruence have not been addressed. Here, we use twelve nuclear loci, representing eleven protein coding genes (of which ten are autosomal and one X-linked in D. melanogaster) and one non-coding region (X-linked in D. melanogaster), to test for phylogenetic incongruence and to investigate its causes. Within the melanogaster subgroup, we use sequences from D. melanogaster, D. simulans, D. yakuba, D. teissieri, and D. erecta. D. eugracilis and D. lutescens serve as representatives of the eugracilis and takahashii subgroups, respectively. We use sequences from D. pseudoobscura and D. ananassae as outgroups.

Using maximum parsimony, maximum likelihood, and Bayesian phylogenetic reconstruction methods, we find strong support for Topology II (D. yakuba/D. teissieri + D. erecta/D. orena) within the melanogaster subgroup. Relationships among the melanogaster, eugracilis, and takahashii subgroups remain equivocal, however, with different loci supporting different tree topologies. Using the likelihood heterogeneity test (LHT) of Huelsenbeck and Bull (1996), we find statistically robust evidence for topological incongruence between loci, which we argue cannot be attributed to a variety of potential confounding factors. In light of the difficulty in resolving relationships between these three subgroups, in this and other studies, we propose that these lineages may have speciated rapidly from a common, polymorphic ancestor, such that lineage sorting resulted in incongruent trees for different gene regions (Pamilo and Nei, 1988). Interestingly, we find evidence for intralocus recombination in the common ancestor of the melanogaster, eugracilis, and takahashii subgroups, and in the common ancestor of the melanogaster subgroup. We discuss the possible implications of such complex histories for inferences of tree topology, substitution rates, and positive selection.

Materials and Methods

Drosophila Strains, DNA Sequences, and Sequence Alignment

Most sequences used in this study have been previously published, and were obtained from public databases (Table 1). Several additional sequences were collected for this study, from the following strains kindly donated by Andrew Clark (Cornell University): D. erecta (S-18; originally from the Ashburner laboratory), D. eugracilis (Tucson Drosophila Stock Center 451.3), D. lutescens (271.1), D. teissieri (257.0), and D. yakuba (261.0). D. simulans sequences were from an Australian iso-female line collected in December, 1997 by Ary Hoffmann. Partial coding sequences for CG3066, CG7415, CG4928 were used by Swanson et al. (2004) for inferences of positive selection. Sequences from additional species for these genes have been deposited in GenBank under the following accession numbers: DQ907915, DQ907916, and DQ907923. The full coding sequence of mitch was obtained from GenBank for all species except D. ananassae. Sequence for D. ananassae was obtained from the public sequencing effort (http://species.flybase.net). Sequences for CG9336 and the non-coding locus seq211 have not been previously published, and have been deposited in GenBank under accession numbers DQ907917- DQ907922, and DQ907924- DQ907929. Sequences for Adh, Adhr, Gld, and ry were obtained from Ko et al. (2003), with the exception of sequences from D. ananassae, which were obtained from the public sequencing effort. hunchback (hb) sequences are from (Schawaroch, 2002), and Iris sequences are from Malik and Henikoff (2005). Sequence alignments for coding regions were performed using the ClustalW algorithm, as implemented in MegAlign (DNASTAR, Inc.), and were modified by eye to maximize amino acid identity. The non-coding locus seq211 was aligned using MAVID (Bray and Pachter, 2004).

Table 1.

Loci used in this study

Locus	Coding/Non-coding	Genomic location in D. melanogastera	Length	Reference	Tree lengthb
Adh	coding	2L (35B3)	834	Ko et al. (2003)	0.57
Adhr	coding	2L (35B3)	875	Ko et al. (2003)	0.88
ry	coding	3R (87D9)	4098	Ko et al. (2003)	0.99
Gld	coding	3R (84D3)	1549	Ko et al. (2003)	0.85
mitch	coding	3 (87D5)	699	Goldberg et al. (unpublished)	1.79
hb	coding	3R (85A5)	534	Schawaroch (2000)	1.61
CG3066	coding	3R (84D14-E1)	872	This study	1.42
CG4928	coding	X (15C1-4)	1536	This study	0.43
CG7415	coding	3R (84F13)	788	This study	1.02
CG9336	coding	2L (38F3)	378	This study	0.67
seq211	non-coding	X (3C5)	2859	This study	1.25
Iris	coding	2L (21F1)	1620	Malik and Henikoff (2005)	2.53

^aChromosome arm and cytological band.

^bTotal tree length in expected substitutions per site, from the maximum likelihood tree.

Tests for Saturation and Base Compositional Bias

We tested for substitutional saturation, in order to assess the potential effects of homoplasy on phylogenetic inferences. Following Engstrom et al. (2004), for each locus, the uncorrected distance (p) between each pair of species was plotted against the maximum likelihood corrected distance (ML). A positive relationship is expected for unsaturated data, while saturated data plateau at higher levels of divergence. To identify such a plateau, we fitted a second order polynomial to each of the saturation plots using the statistical package JMP IN 5.1 (Duxbury). We then identified the maximum of the regression line, which represents the point at which a positive relationship no longer exists between p and ML. Data points to the right of the maximum suffer from saturation, raising homoplasy as a concern.

For each locus, chi-squared tests for base frequency equilibrium across all species (including outgroups) were performed using PAUP*4.0b10 (Swofford, 2002).

Phylogenetic Inference

Maximum parsimony and maximum likelihood analyses were performed using PAUP*4.0b10 (Swofford, 2002). For individual locus analyses and for the concatenated alignment, maximum likelihood analyses were performed under the general time reversible model of nucleotide substitution, with gamma distributed rates, allowing for invariant sites (GTR+G+I; Felsenstein, 1981; Yang, 1994). MrBayes 3.0b4 was used for Bayesian phylogeny estimation (Huelsenbeck and Ronquist, 2001; Ronquist and Huelsenbeck, 2003). We again used the GTR+G+I model of nucleotide substitution. In single locus analyses, four Markov chains were run for 100,000 generations of burn-in, followed by 500,000 generations for topology and parameter estimation. For the concatenated data set, four chains were allowed to run for 2,000,000 generations, following 500,000 generations of burn-in.

Interior branch length tests

At each locus, we used likelihood ratio tests (LRT) as implemented in PAUP*4.0b10 (Swofford, 2002) to test for zero branch lengths around two nodes: the node connecting D. eugracilis, D. lutescens, and the melanogaster subgroup, and the node connecting D. erecta, the D. simulans/D. melanogaster species pair, and the D. yakuba/D. teissieri species pair. In this LRT, the null hypothesis (H₀) is that the branch in question has zero length (i.e., that the relevant node is a molecular polytomy). The alternative hypothesis (H_A) states that the branch has a positive length. The LRT test statistic, 2[ln(L_H0) − ln (L_HA)], where L_H0 and L_HA represent the likelihoods of H₀ and H_A respectively, follows a 50:50 mixture distribution of the χ² with 0 degrees of freedom and the χ² with 1 degree of freedom (Goldman and Whelan, 2000; Slowinski, 2001).

Statistical tests of incongruence

We performed two tests of incongruence. First, we applied the incongruence length difference (ILD) test (Farris et al., 1995), as implemented under the partition homogeneity test in PAUP*4.0b10 (Swofford, 2002). This commonly used test compares the length of the most parsimonious tree under user defined data partitions (here, different loci) to the length of the most parsimonious tree for the combined data. The null distribution is obtained by creating new partitions of the same size as the user defined partitions at random from the original dataset. One thousand bootstrap replicates were used for the null distribution.

Since the ILD test may reject the null hypothesis of congruence for reasons other than topological incongruence (e.g., Darlu and Lecointre, 2002), and does not readily allow for localization of incongruence to specific nodes, we implemented the LHT of Huelsenbeck and Bull (1996). The null hypothesis (H₀) of the LHT states that the same topology underlies all data partitions (in this case, different loci), while the alternative hypothesis (H_A) allows different partitions to have different topologies; the LHT thus allows for direct testing of topological incongruence in a likelihood framework. Under both H₀ and H_A, other model parameters, e.g., branch lengths and gamma shape parameters, are free to vary among partitions. The LHT compares the likelihood under the null hypothesis (L₀) to the likelihood under the alternative hypothesis (L_A), using the test statistic

$$\delta =ln{L}_0-ln{L}_A.$$

We calculate the null distribution of δ by parametric bootstrapping (Huelsenbeck and Bull, 1996), although other approaches are possible (Waddell et al., 2000).

In order to test for topological heterogeneity within the melanogaster subgroup, maximum likelihood parameter estimates and likelihood scores were obtained under Topologies I, II, and III for each locus individually, under the GTR+G+I model of substitution, using PAUP*4.0b10 (Swofford, 2002), and δ was calculated as above. Parametric bootstrap replicates were generated by simulation under the GTR+G+I model using SeqGen v. 1.1, using the ML parameter estimates for each locus, under the single topology that maximizes the likelihood summed over all loci (Topology II; see Results). D. pseudoobscura and D. ananassae were not used for this analysis, in order to reduce computational time. D. eugracilis and D. lutescens are therefore the outgroups for this analysis. Since all inference was conducted on unrooted trees, lack of resolution at this basal node should not be an issue. A similar procedure was used to test for topological heterogeneity between the melanogaster, eugracilis, and takahashii subgroups. Here, D. pseudoobscura and D. ananassae were used as outgroups, and D. erecta was not included. The null distribution was generated using Topology C (see Results).

Tests for Recombination

We tested for intralocus recombination in the common ancestor of the melanogaster subgroup, as well as in the common ancestor of D. eugracilis, D. lutescens, and D. melanogaster. To do so, we used a Bayesian Hidden Markov Model (HMM-Bayes) approach (Husmeier and McGuire, 2003), as implemented in TOPALi (Milne et al., 2004). Under standard models of DNA evolution, the probability of observing a particular column y_t in a DNA multiple sequence alignment of n nucleotides is given by P(y_t|S, w, Θ), where t is the site label (1 to n), S is the tree topology, w is a vector of branch lengths, and Θ represents the parameters of the chosen model of nucleotide substitution. Whereas it is typically assumed that there is one “true” topology for all n sites in a locus, the HMM-Bayes approach allows each site to have a different topology. Topology is treated as a random variable S_t that depends on the site label t. The state space of S_t consists of all possible unrooted topologies for the sequences under consideration, i.e., there are three possible states for any alignment of four sequences. HMM-Bayes uses a Monte Carlo Markov Chain approach to find the state sequence Ŝ that is best supported by the data. Recombination events are detected as changes in state along the alignment. If recombination has occurred, then different contiguous portions of an alignment may support different tree topologies.

Due to computational limitations, TOPALi only accepts alignments of four sequences. In order to test for intralocus recombination in the common ancestor of the melanogaster subgroup, we used gene sequences from D. melanogaster, D. erecta, D. yakuba, and D. lutescens as an outgroup. In order to test for intralocus recombination in the common ancestor of D. eugracilis, D. lutescens, and D. melanogaster, we used sequences from these three species, and D. pseudoobscura as an outgroup. Alignments for all twelve loci described above were analyzed by HMM-Bayes.

Results

Tests for Saturation and Base Compositional Bias

Using saturation plots, we find no evidence of substitutional saturation for the ingroup taxa at any locus (Fig. 3 shows two example plots, with distances between ingroups represented by black squares; other data not shown). Thus, excessive homoplasy should not be a major concern for phylogenetic inference within the D. melanogaster subgroup. At three loci (mitch, Gld, and hb), there is evidence for some saturation between the ingroup and outgroup taxa. Base composition equilibrium was rejected at two loci, ry (P < 0.0001) and Iris (P < 0.0001). We note that Ko et al. (2003) found little impact of this non-equilibrium base composition on phylogenetic inferences using ry; we give further consideration to the potential implications of saturation and non-equilibrium base composition below.

Figure 3.

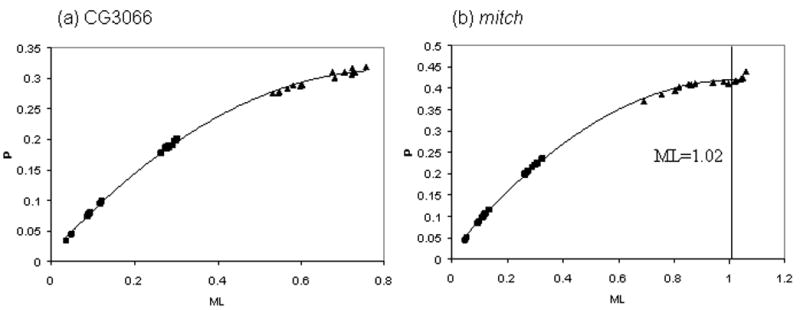
Saturation plots of (a) CG3066 and (b) mitch. Uncorrected distances (p) between each pair of taxa were plotted against the maximum likelihood corrected distance (ML). Black squares represent distances between ingroup taxa only, while triangles involve at least one outgroup taxon. The fitted line is the best fit second order polynomial, and the vertical line in (b) represents the maximum. To the right of the maximum, substitutional saturation is evident.

Phylogenetic Inference

Phylogenetic analyses were conducted on all twelve single locus datasets, as well as on a concatenation of all twelve loci. Figure 4 summarizes the results of phylogenetic reconstructions for all loci except Adh, Adhr, Gld, and ry; results for the latter genes do not differ substantially from those of Ko et al. (2003), and so are not shown here (topologies are described below). Figure 5 shows the majority-rule tree and maximum likelihood tree with branch lengths for the concatenated data set. In general, maximum parsimony (MP), maximum likelihood (ML) and Bayesian (B) methods yielded similar tree topologies within a dataset; exceptions are noted below.

Figure 4.

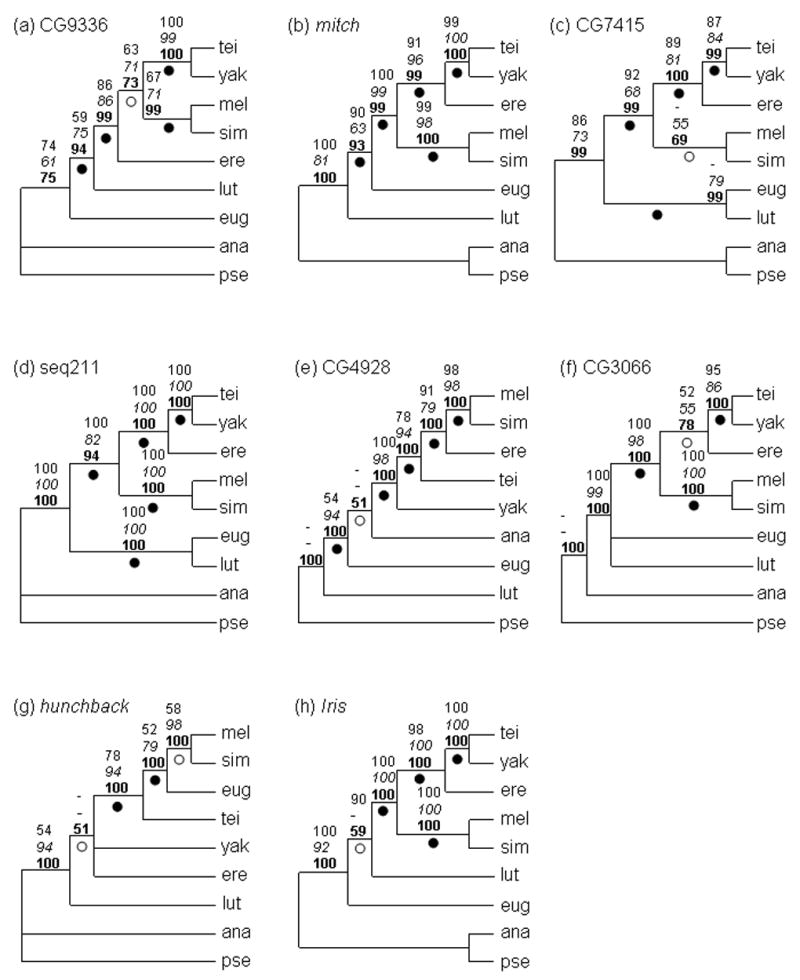
Consensus trees for single locus analyses. The numbers above each node indicate, from top to bottom, maximum parsimony bootstrap score (1000 replicates), maximum likelihood bootstrap score (italic; 100 replicates), and Bayesian posterior clade probability (bold; 500000 generations). For hunchback, the three tree construction methods disagree, and the Bayesian consensus tree is shown (see results section). (a) CG9336. (b) mitch. (c) CG7415. (d) seq211. (e) CG4928. (f) CG3066. (g) hunchback. (h) Iris. Zero branch length tests were carried out as described in Materials and Methods; open dots represent branches that fail to reject the null hypothesis of zero branch length at a cutoff of 0.05. Black dots represent branches that were tested and do reject the null hypothesis.

Figure 5.

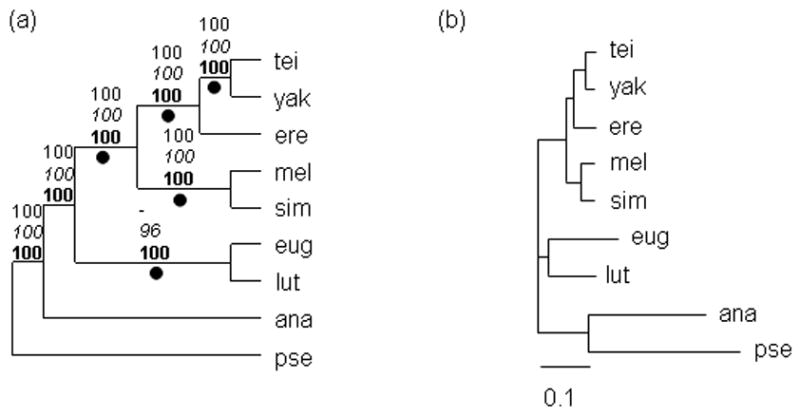
(a) Consensus tree for multi-locus analysis. Branch labels are the same as Figure 4. (b) Phylogram for the multi-locus analysis. The scale bar represents 0.1 expected substitutions per site.

Relationships within the melanogaster subgroup

Within the melanogaster subgroup, phylogenetic reconstructions using single loci yielded several different tree topologies (Fig. 4). Different reconstruction methods were generally consistent for a given locus. Topology II, according to which D. erecta shares a most recent common ancestor with the D. yakuba- D. teissieri species pair to the exclusion of D. melanogaster-D. simulans, is supported by five of the eight loci presented in Figure 4: mitch, CG7415, CG3066, seq211, and Iris. With the exception of CG3066, bootstrap scores are high (>80%) for all loci, as are Bayesian clade probabilities (>99%). Topology I, whereby D. erecta is basal within the melanogaster subgroup, is supported by CG9336. Bootstrap scores and Bayesian clade probabilities are, however, relatively low (MP: 63%; ML: 71%; B: 73%). CG4928 supports Topology III, which groups D. erecta together with the D. melanogaster-D. simulans species pair, with fairly strong support (MP: 91%; ML: 79%; B:100%). However, CG4928 also fails to group D. yakuba and D. teissieri as sister species. Finally, analysis of hb fails to support monophyly of the melanogaster subgroup, placing D. eugracilis as a sister taxon to the D. melanogaster-D. simulans species pair. Bootstrap scores are quite low for most clades, although Bayesian posterior probabilities are high.

Re-analysis of the four genes studied by Ko et al. (2003) using D. ananassae as an additional outgroup did not alter tree topologies within the melanogaster subgroup. As in Ko et al. (2003), Adhr, Gld, and ry all support Topology II, whereas Adh gives weak support for Topology III (data not shown).

Topology II is strongly supported by a concatenation of all twelve loci examined here (Fig. 5). Bootstrap scores and the Bayesian clade probability for the (D. yakuba/D. teissieri + D. erecta) grouping are all 100%, indicating robust support for monophyly of this clade.

Relationships between subgroups

Different loci yield different tree topologies with respect to the relationships between D. lutescens, D. eugracilis, and the melanogaster subgroup. Topology A, which places D. eugracilis closer to the melanogaster subgroup than D. lutescens, is supported by two coding loci, mitch and CG4928. The degree of support for this branching order varies by method, however, with low maximum likelihood and maximum parsimony bootstrap scores for mitch (ML: 63%) and CG4928 (MP: <50%), respectively. All three tree reconstruction methods fail to place D. ananassae as an outgroup for CG4928. Topology B, which places D. lutescens closer to the melanogaster subgroup, is weakly supported by CG9336, CG3066, and Iris. Maximum parsimony and maximum likelihood bootstrap scores for CG9336 are low (MP: 59%; ML: 75%), while the Bayesian clade probability is high (B: 94%). For CG3066 and Iris, bootstrap scores and Bayesian clade probabilities are generally low (CG30666 - MP: 55%; ML: 39%; B: 43%; Iris – MP: 90%; ML: 50%; B: 59%). Finally, two loci, CG7415 and seq211, support Topology C, according to which D. eugracilis and D. lutescens form a group that is monophyletic with respect to the D. melanogaster subgroup. This topology is strongly supported by all methods for seq211, but gains mixed support from CG7415.

Ko et al. (2003) found that different tree reconstruction methods yielded incongruent results for Adh, Adhr, Gld, and ry. The same general outcome is reached here; different reconstruction methods are consistent only for ry, which supports Topology C. No topology is strongly supported by Adh. Adhr supports Topology A when analyzed using Bayesian analysis, but Topology B under maximum parsimony. Parsimony analysis of Gld also supports Topology B, but maximum likelihood and Bayesian analyses support Topology C.

For the concatenated dataset, maximum likelihood and Bayesian methods give strong support to Topology C, with a well supported D. eugracilis-D. lutescens clade. Maximum parsimony, by contrast, weakly supports Topology B (MP: 66%). We note that inference on the concatenated dataset should be treated with caution, however. For example, one assumption of the Bayesian Markov chain Monte Carlo (MCMC) approach used by MrBayes, that there is a single phylogeny for all sites, is clearly violated in this analysis. Different sites support different tree topologies, and such mixtures of trees are known to confound MCMC methods (Mossel and Vigoda, 2005). The behavior of other tree reconstruction methods has not been analyzed for mixture models of this variety, but may be similarly confounded.

Interior branch length tests

Interior branches that fail to reject the null hypothesis of zero branch length at a cutoff of α=0.05 are indicated in Figures 4 and 5 with an open dot, while branches that were tested but do reject the null hypothesis are marked with a black dot. Within the melanogaster subgroup, one or more branches are not significantly different from zero in length for CG9336, CG7415, and hb. For most loci, zero branch length is rejected for the branches connecting D. eugracilis, D. lutescens, and the melanogaster subgroup (with the exception of Iris).

Tests of incongruence

Applied to all twelve loci considered in this study, the ILD test of Farris et al. (Farris et al., 1995) rejects the null hypothesis of homogeneity (P < 0.002). While this result does suggest incongruence among loci, it may be difficult to distinguish rejection due to topological incongruity, rate heterogeneity between loci, or other factors (Barker and Lutzoni, 2002; Darlu and Lecointre, 2002; Dolphin et al., 2000). Thus, in order to explicitly test for topological incongruence, and to specifically investigate disagreement at the two nodes of interest here, we implemented the LHT of Huelsenbeck and Bull (1996).

Using the LHT, we tested for incongruence with respect to the placement of D. erecta in the melanogaster subgroup, and the relationships between the melanogaster, eugracilis, and takahashii subgroups (Table 2, Fig. 6), again using all twelve loci. Within the melanogaster subgroup, if a single tree is assumed to underlie all loci, Topology II is the maximum likelihood topology (Table 2). When the assumption that a single tree underlies all loci is relaxed, such that each locus is allowed any of three possible topologies, an improvement of 7.18 likelihood units is observed (δ = 7.18; Table 2). The null distribution of δ was obtained by parametric bootstrapping on Topology II (Fig. 6a). Five hundred replicates were performed. Only two replicates had a value of δ more extreme than 7.18 (P = 0.004), indicating that the degree of incongruence present in the empirical dataset is unlikely to arise purely from sampling error. In order to identify the source of this incongruence, we excluded single loci from the analysis and re-calculated δ and its null distribution. When CG4928 was excluded, we no longer detected significant incongruence (δ = 2.29; P = 0.122), while no other single locus had a similar effect on the test result (data not shown). We suggest that the low rate of substitution at CG4928 (Table 1), combined with a short internal branch between D. erecta and its relatives, has led to a misleading phylogenetic signal at this locus.

Table 2.

Likelihood heterogeneity test - Negative log likelihoods under the GTR+G+I model of substitution.

	Loci
Topology	Adh	Adhr	ry	Gld	mitch	hb	Iris	CG3066	CG4928	CG7415	CG9336	seq211	Total
Ia	1836.41	2394.61	11919.72	4653.70	2407.76	1160.64	7629.75	2967.78	3556.16	2201.19	1041.72 c	5996.76	47766.22
II	1836.23	2385.77c	11899.85c	4651.21c	2399.87c	1160.63	7616.29c	2966.24c	3556.16	2196.22 c	1041.96	5979.46 c	47689.88c
III	1834.20c	2394.61	11921.53	4655.43	2407.73	1160.60	7631.21c	2967.84	3551.27c	2201.32	1041.99	5996.76	47764.51
										δ1d = 47689.88 − 47682.70 = 7.18 (P = 0.004)
Ab	2406.89c	3154.87c	15915.77	5881.95	3578.56c	1713.58	10413.70c	4101.74	4618.44c	2883.71	1333.56	8507.18	64509.96
B	2407.79	3156.20	15920.83	5880.39	3580.44	1716.06	10413.23c	4101.40	4620.91	2883.39	1331.48 c	8507.18	64519.30
C	2410.39	3156.40	15902.15c	5879.06c	3580.92	1716.05	10414.03	4100.79c	4618.71	2877.92 c	1333.56	8492.48 c	64482.47c
										δ2d = 64482.47 − 64469.46 = 13.01 (P < 0.002)

^aFor comparison of Topologies I, II, and III, D. pseudoobscura and D. ananassae were excluded.

^bFor comparison of Topologies A, B, and C, D. erecta was excluded.

^cValue for the maximum-likelihood tree.

^dδ₁ is the LHT test statistic for comparison between Topologies I, II, and III, and δ₂ is the LHT test statistic for comparison between Topologies A, B, and C.

Figure 6.

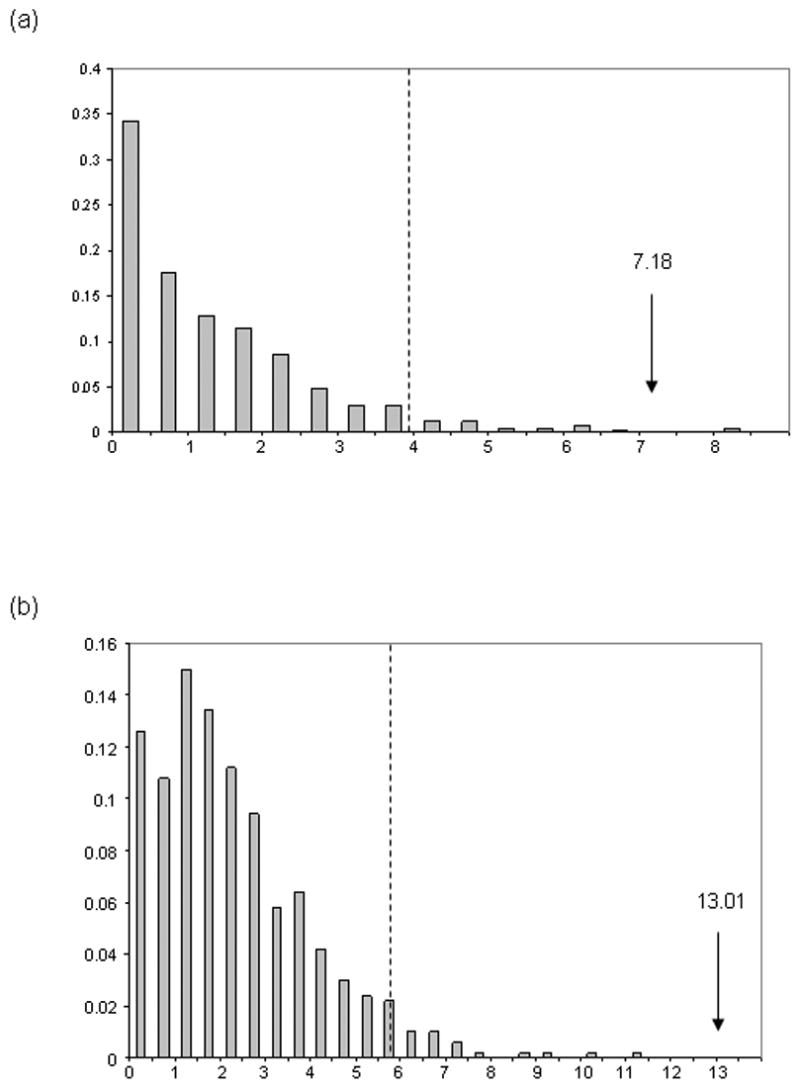
Simulated null distributions of δ for tests of topological heterogeneity (a) within the melanogaster subgroup and (b) between the melanogaster, eugracilis, and takahashii subgroups. 500 bootstrap replicates were simulated under the hypothesis that a single tree underlies all 12 loci, using maximum likelihood parameter estimates for the original data. The observed values of δ (indicated by a vertical arrow) both fall outside the 95% confidence intervals (dashed line), indicating rejection of the null hypothesis.

With respect to relationships among subgroups, Topology C provides the best single topology under the null hypothesis (Table 2); relaxation of the assumption of a single underlying tree provides an improvement of 13.01 likelihood units (δ = 13.01; Table 2). Analysis of 500 simulated datasets suggests that this value of δ is very unlikely to occur by chance (P < 0.002; Fig. 6b). Thus, we reject the null hypothesis that a single topology underlies all twelve loci. Exclusion of single loci did not result in a non-significant test-statistic (data not shown). Moreover, we attempted to assess the impacts of homoplasy, non-equilibrium base composition, and positive selection by excluding loci showing evidence for saturation between outgroup and ingroup taxa, loci rejecting base composition equilibrium, or loci showing evidence for positive selection across numerous taxa (CG3066 and Iris; Malik and Henikoff, 2005; Swanson et al., 2004). In each case, the null hypothesis is still rejected, suggesting that none of these potential confounding factors is solely responsible for the observed level of incongruence.

Evidence for recombination within genes

We used a Bayesian approach to find evidence of recombination events in the common ancestor of the melanogaster subgroup, and in the common ancestor of D. eugracilis, D. lutescens, and D. melanogaster. Using TOPALi (Milne et al., 2004), we found statistically significant evidence for recombination at three loci out of twelve tested (Fig. 7; other data not shown). We find evidence for intralocus recombination in the common ancestor of D. melanogaster, D. eugracilis, and D. lutescens at mitch (Fig. 7a), and at the non-coding locus seq211 (results not shown). In addition, we find evidence for intralocus recombination in the common ancestor of the melanogaster subgroup species at Iris (results not shown) and at seq211 (Fig. 7b). We note that this analysis is largely exploratory, since the performance of the HMM-Bayes method has not been rigorously tested under a variety of conditions (including, importantly, situations where homoplasy may arise).

Figure 7.

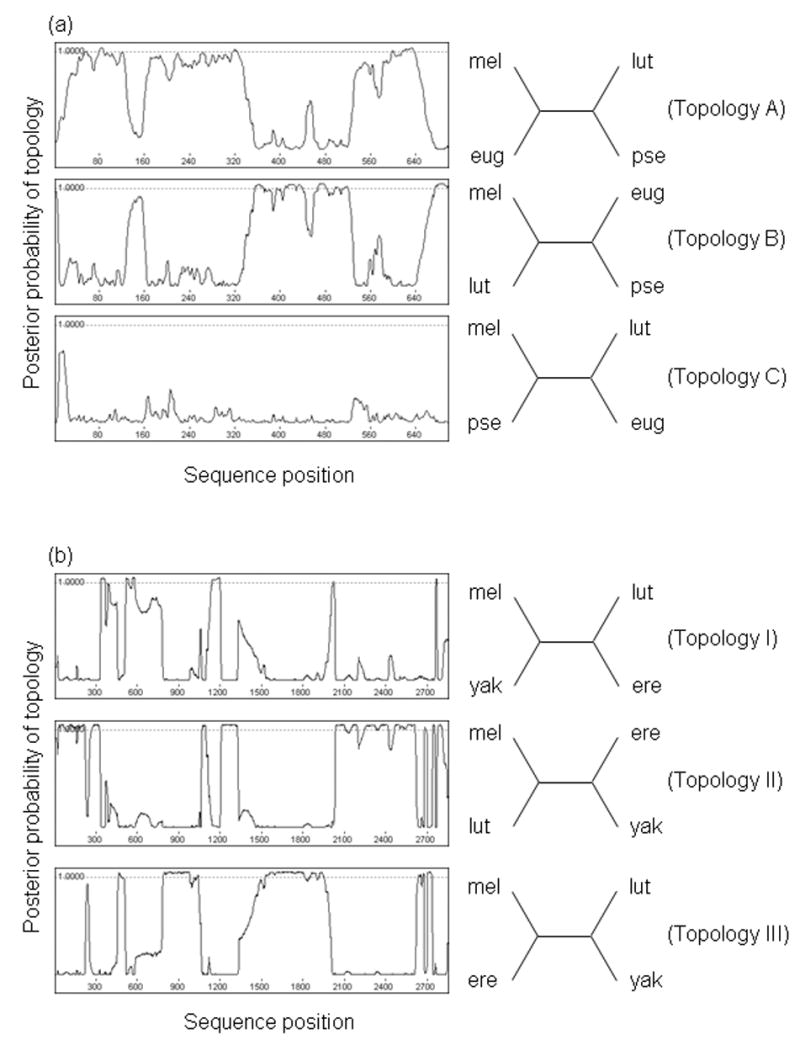
Evidence for ancestral lineage sorting with recombination. The plots on the left indicate, across the length of the locus, the posterior probability of each of the topologies shown on the right. (a) mitch supports two different tree topologies, A and B, for the relationship between D. lutescens, D. eugracilis, and the melanogaster subgroup. (b) seq211 supports all three possible topologies in the melanogaster subgroup.

Discussion

Phylogenetic relationships within the melanogaster subgroup

Phylogenetic relationships within the melanogaster species group and subgroup have proven difficult to resolve (Ko et al., 2003; Kopp, 2006; Kopp and True, 2002b; Lewis et al., 2005). In this study, we find strong support for Topology II within the melanogaster subgroup, i.e., for the existence of a clade consisting of D. erecta and the D. yakuba-D. teissieri species pair, to the exclusion of D. melanogaster and D. simulans. In individual locus analyses, eight out of twelve loci support this topology (Fig. 4; Table 2). Moreover, LHT results suggest that one gene, CG4928, is primarily responsible for any statistically significant incongruence between loci; exclusion of CG4928 results in a non-significant test statistic. In addition, analysis of a concatenated dataset consisting of over 18 kb of sequence provides statistically robust support for Topology II (Fig. 5). Notably, all multi-locus datasets analyzed to date give the same phylogenetic reconstruction (Ko et al., 2003; Kopp and True, 2002b), as do numerous independent single locus analyses (Arhontaki et al., 2002; Gailey et al., 2000; Nigro et al., 1991; Pelandakis et al., 1991). The prevailing alternative hypothesis, whereby D. erecta occupies a basal position within the melanogaster subgroup (Topology I), is supported by allozyme distance data (Cariou, 1987), sequence analysis of Adh in early studies (Jeffs et al., 1994; Russo et al., 1995) and by biogeographical considerations (Lachaise et al., 1988). The weight of evidence, we argue, is in favor of Topology II.

Phylogenetic relationships between subgroups

The data presented here fail to unambiguously resolve the relationship between D. eugracilis, D. lutescens, and the melanogaster subgroup. In analyses of individual loci and concatenated datasets, tree topology is strongly dependent on choice of locus: of the twelve loci considered in this study, no more than five support any one of the three possible trees (Fig. 4; Table 2). Topology C is strongly supported by the concatenated alignment in model-based analyses, while maximum parsimony yields weak support for Topology B. Similarly, disagreements are common amongst previous studies: Ko et al. (2003), using four loci, argue for Topology A. By contrast, Kopp and True (2002b) find support for Topology B, using data from six loci.

Using the LHT, we find strong evidence for topological incongruence between loci with respect to relationships between subgroups (Fig. 6; Tables 2 and 3). This incongruence is not attributable to any single locus. Moreover, we find no evidence that homoplasy, non-equilibrium base composition, or positive selection is responsible for the signal of incongruence, since tests excluding loci with evidence for any of these factors still reject the null hypothesis (Table 3).

Table 3.

Values of δ₂ and associated probabilities for subsets of loci.

Subset	Loci removed	δ2	P
All loci	None	13.01	<0.002
Loci with no evidence of saturation between outgroup and ingroup taxa	Gld, hb, mitch	8.17	0.004
Loci with no evidence for base compositional disequilibrium	ry, Iris	12.21	<0.002
Loci with no evidence for positive selection	CG3066, Iris	12.21	<0.002

Species level polytomies in the melanogaster species group

It is well documented that gene trees do not always recapitulate the species tree (e.g., (Degnan and Salter, 2005; Pamilo and Nei, 1988; Poe and Chubb, 2004; Wu, 1991; Degnan and Rosenberg, 2006). One potential reason for such disagreement is sorting of polymorphism in the common ancestor of three or more lineages. Consider the case of three species, A, B, and C, that diverged from a common ancestor, and orthologous gene sequences a, b, and c sampled from these species in the present. Suppose that C diverged first from the common ancestor, and that B subsequently diverged from the lineage leading to A, such that the rooted species tree is appropriately represented as ((A, B), C). In order for the gene tree to recapitulate the species tree, a and b must find a common ancestor (coalesce) before either coalesces with c. The gene tree will fail to accurately represent the species history if a coalesces with c before either coalesces with b, or if b coalesces with c before either coalesces with a.

Pamilo and Nei (1988) showed that, for a neutral locus, the probability P that a gene tree has the same topology as the species tree is dependent on only two factors: population size N, and time t between speciation events. Time to fixation for ancestral polymorphisms is higher for large populations; as such, P is smaller for higher values of N. A longer period of time between speciation events gives polymorphisms more time to go to fixation; hence, P is higher for larger values of t. Importantly, then, a short period of time between subsequent speciation events substantially decreases the probability that the gene tree recapitulates the species tree. Towards the limiting case of a polytomy (splitting of an ancestral lineage simultaneously into three or more daughter lineages), the probability that the gene tree has the same topology as the species tree is only 1/3 in the case of three daughter lineages. Thus, multiple loci sampled from lineages that diverged simultaneously (or nearly so) should show different tree topologies. Incongruence between loci has been cited as evidence for simultaneous or near-simultaneous radiation in, for example, birds (Poe and Chubb, 2004) and primates (Ruvolo, 1997).

Given this prediction, there are at least two potential species level polytomies in the melanogaster species group: One at the root of the melanogaster subgroup, and one connecting D. eugracilis, D. lutescens, and the melanogaster subgroup. We can use incongruence between gene trees to test the hypothesis of a species level polytomy, following Ruvolo (1997). Consider three species A, B, and C, with the same r independent loci sampled from each one. Suppose that the real species tree is ((A, B), C). For each locus, there are three possible rooted gene trees: ((a, b), c), ((a, c), b), and ((b, c), a). Following Pamilo and Nei (1988), call these topologies α, β, and γ, respectively, and let i, j, and k represent the number of independent loci supporting topologies α, β, and γ. The correct topology is inferred if i>j and i>k. We can determine if i is greater than the number of loci that would be expected to support topology α under the null hypothesis of a strict polytomy, as follows. Under a polytomy, each topology has an equal probability (1/3) of being realized, such that the probability of obtaining the true topology (α) is 1/3, and the probability of obtaining the wrong topology (β or γ) is 2/3. The probability that i or more of the r loci support the true topology is therefore given by a sum of binomial probabilities:

$$P(i)=\underset{n=i}{\overset{r}{\Sigma }}\left(\begin{array}{c}r\\ n\end{array}\right){(1/3)}^n{(2/3)}^{r-n}$$

Failure to reject the null hypothesis indicates that the available data are consistent with polytomy at the species level. Rejection of the null hypothesis, by contrast, suggests that the available data are inconsistent with simultaneous speciation events.

Using gene trees inferred in this and other studies, we can evaluate the probability of a polytomy at the two branch points described above (see Supplementary Material Table 1 for genes, references, and topologies). We note that this approach is approximate, as it fails to take into account uncertainty in individual tree topologies (Satta et al., 2000). Nonetheless, it should provide some quantitative sense of the robustness of phylogenetic hypotheses. For relationships within the melanogaster subgroup, 13 genes support Topology II and 3 do not. Under a polytomy, the probability that 13 or more genes out of 16 will support a single topology is 0.000116; hence, we reject the null hypothesis at this branch point. Our LHT results similarly suggest broad topological congruence between loci concerning relationships within the melanogaster subgroup.

By contrast, for relationships between the melanogaster, eugracilis, and takahashii subgroups, 6 genes support Topology A, 5 support Topology C, and 3 support Topology B. The null probability that 6 or more genes out of 14 will support a single topology is 0.31, and hence a species level polytomy cannot be rejected. The data are thus consistent with lineage sorting from the common ancestor of the melanogaster, eugracilis, and takahashii subgroup through closely spaced speciation events. This finding is also consistent with our LHT results, wherein significant incongruence between loci could not be attributed to any single locus or to various potential confounding factors. A recent study (Kopp 2006) argued that the ancient (12–24 mya) divergence of the melanogaster species group renders lineage sorting unlikely. However, we note that the relevant time interval for lineage sorting is not the age of divergence, but rather the time between closely spaced speciation events. Lineage sorting in the deep history of a clade may still result in incongruence between loci, as subsequent coalescence of alleles within a lineage will not resolve relationships in the ancestral population. We argue that an ancient lineage sorting event is the best explanation for our results, as well as for Kopp’s (2006) finding that relationships between D. melanogaster, D. eugracilis, and D. biarmipes (a close relative of the takahashii subgroup) are poorly supported.

We therefore conclude that, within the melanogaster subgroup, there is strong support for a monophyletic clade consisting of the D. yakuba-D. teissieri species pair and the D. erecta-D. orena species pair (although D. orena was not examined in this study, we assume here that it is the sister species to D. erecta). However, we note that the internal branches connecting the melanogaster-simulans, teissieri-yakuba, and erecta-orena species pairs tend to be short (Fig. 4), and may present some risk of lineage sorting. We argue that Topology C is the best current hypothesis for the speciation history of the melanogaster, eugracilis, and takahashii subgroups, being supported both by partitioned data analysis (Table 2) and the combined data (Fig. 5). Nonetheless, incongruence between loci is widespread, and may be best explained by extensive lineage sorting from a polymorphic ancestor.

Implications for comparative studies

Phylogenetic incongruence within and between loci, of the sort observed in this study, is a potential concern in several lineages of interest to evolutionary biologists. The relationship among humans, chimpanzees, and gorillas is perhaps the best known example. These three primate lineages almost certainly speciated rapidly from a common ancestor, and as a result, different loci provide support for each of three possible rooted tree topologies (Ruvolo, 1997; Satta et al., 2000). Moreover, different sites within a given locus may support different topologies (Satta et al., 2000). Another well documented example of lineage sorting comes from the D. simulans species complex, which includes D. simulans, D. mauritiana, and D. sechellia. Here, speciation is thought to have occurred fairly recently, such that some ancestral polymorphism is shared between species (Kliman et al., 2000). Only two loci have been identified that support monophyly of alleles within species, and the species relationships that they support are different (Ting et al., 2000; Malik and Henikoff, 2005). In addition, full genome sequences are now available for several members of the melanogaster subgroup (http://species.flybase.net), and thus will be subject to extensive comparative analyses. We have argued that the lineages giving rise to the sequenced species D. erecta, D. yakuba, and (D. melanogaster + D. simulans) may have split in rapid succession, resulting in some lineage sorting and intralocus recombination. Sorting from a polymorphic ancestor, as observed in primates and in several Drosophila lineages, has several implications for comparative studies, three of which we highlight here.

First, phylogenetic inference itself can be complicated by incongruence within and between loci. It is generally acknowledged that single locus analyses are insufficient to resolve species relationships, such that data must be collected from multiple loci in order to make robust inferences. Authors have debated whether multi-locus datasets should be analyzed on a locus-by-locus basis, or whether it is more appropriate and/or powerful to concatenate all loci (e.g., Huelsenbeck et al., 1996; Kluge, 1989; Miyamoto and Fitch, 1995). Advocates of the so-called “total evidence” approach, whereby all data are included in a combined analysis, argue on philosophical grounds about explanatory power (Kluge, 1989), or suggest that use of a concatenated dataset allows the dominant phylogenetic signal to “overwhelm” conflicting signals (Rokas et al., 2003). Lineage sorting events may be especially problematic for total evidence approaches, and should be treated with caution generally. For example, a recent study demonstrated that popular MCMC methods perform poorly on datasets containing mixed phylogenetic signals, taking inordinately long to converge on the true tree (Mossel and Vigoda, 2005). Moreover, in some cases where more than three lineages have been affected by lineage sorting, sampling of multiple loci can converge on the wrong species tree in total evidence or locus-by-locus analyses (Degnan and Rosenberg, 2006). Such scenarios are especially likely in speciose clades where large population sizes are common (like Drosophila), and necessitate careful analytical procedures. Finally, important information about speciation history can be lost by the use of a concatenated dataset. The presence of extensive incongruence can reveal complex genealogical history, and this will be evident only in multiple single locus analyses and explicit tests of congruence between partitions.

Inference of substitution rates may also be affected by lineage sorting. Consider a case where three species, A, B, and C, arise in rapid succession from a common ancestor, such that polymorphism is shared between them in the early stages of speciation. Here, two mutations in the common ancestor of A, B, and C occurring at partially linked or unlinked sites may give rise to three haplotypes: two haplotypes bearing single mutations, and a recombinant haplotype bearing both. Since polymorphism is initially shared following speciation, a real possibility exists for different haplotypes to go to fixation in each species. Upon sampling gene sequences from A, B, C, we would have to posit recurrent mutation at one of the sites if we were to assume a single tree. Consequently, analyses relying on rate estimates, such as molecular clock inferences and relative rate tests, may be confounded.

Finally, species level polytomies may confound inferences of positive selection, due to the presence of recombination within loci (or between loci for concatenated datasets). Maximum likelihood methods implemented in the popular software package PAML are often used to detect the action of positive selection on coding sequences. These methods are known to be sensitive to recombination; moderate to high levels of recombination can lead to an unacceptably high false positive rate (Anisimova et al., 2003). The increased false positive rate associated with recombination may result from the assumption that the rate of synonymous substitution is homogeneous across all sites (nonsynonymous substitution rates are allowed to vary between codons), or from the use of an incorrect tree for some sites (Anisimova et al., 2003). Although lineage sorting in a deep ancestor has not been explicitly investigated as a source of error in PAML and related analyses, it may have confounding effects.

We suggest several approaches to circumvent inferential problems stemming from ancestral lineage sorting and recombination. First, where possible, we recommend care in the choice of taxa used for studies of molecular evolution. Where three lineages are suspected to have arisen in quick succession from their common ancestor, no more than two should be chosen for analyses dependent on accurate estimates of the substitution rate. In this way, the possibility of all four possible arrangements (including outgroup species) of two biallelic sites appearing in the sample due to recombination is eliminated. Polytomies involving more than three lineages should be treated with extra caution.

Moreover, given that ancestral recombination can lead to conflicting phylogenetic signals and inflation of rate estimates within a locus (Satta et al., 2000; this study), analytical methods that explicitly account for recombination (e.g., Wilson and McVean, 2006) should be used where such histories are a concern. Alternatively, datasets should be examined for intragenic recombination, especially for lineages with histories known to be problematic. Inference may then be conducted on segments supporting the same topology.