Abstract
A theoretical description and experimental validation of the enhanced diffusion weighting generated by selective adiabatic full passage (AFP) pulse trains is provided. Six phantoms (Ph-1 to Ph-6) were studied on a 4T Varian/Siemens whole body MRI system. Phantoms consisted of 2.8 cm diameter plastic tubes containing a mixture of 10 μm ORGASOL polymer beads and 2 mM Gd-DTPA dissolved in 5% agar (Ph-1) or nickel(II) ammonium sulphate hexahydrate doped (56.3 mM – 0.8 mM) water solutions (Ph-2 to Ph-6). A customized localization by adiabatic selective refocusing (LASER) sequence containing slice selective AFP pulse trains and pulsed diffusion gradients applied in the phase encoding direction was used to measure 1H2O diffusion. The b-value associated with the LASER sequence was derived using the Bloch-Torrey equation. The apparent diffusion coefficients measured by LASER were comparable to those measured by a conventional pulsed gradient spin-echo (PGSE) sequence for all phantoms. Image signal intensity increased in Ph-1 and decreased in Ph-2 – Ph-6 as AFP pulse train length increased while maintaining a constant echo-time. These experimental results suggest that such AFP pulse trains can enhance contrast between regions containing microscopic magnetic susceptibility variations and homogeneous regions in which dynamic dephasing relaxation mechanisms are dominant.
Keywords: Adiabatic, LASER, diffusion, b-value, MRI
1. Introduction
Frequency modulated adiabatic full passage pulses can generate a high degree of magnetic spin coherence that is immune to B1 inhomogeneity [1–4]. The localization by adiabatic selective refocusing (LASER) pulse sequence developed by Garwood and DelaBarre [3] exploits this property to achieve sharply defined excitation profiles in single voxel magnetic resonance spectroscopy (MRS) and imaging pulse sequences [5]. However, following excitation, and in the presence of spatial encoding gradients, selective hyperbolic secant (HS) adiabatic full passage (AFP) pulses generate spin phase that is approximately quadratically related to the pulse frequency [6, 7] and therefore approximately quadratically proportional to the spatial coordinate of the spins [8]. This nonlinear phase variation across the selected slice can be compensated [4, 8] to produce robust slice selective AFP π pulses that are immune to RF field inhomogeneity. Conversely, the nonlinear phase dispersion could also be exploited to measure signal loss due to diffusion. However, a preliminary study [9] using the LASER sequence demonstrated that the apparent diffusion coefficient (D) could not be measured accurately in paramagnetic ion doped water phantoms with short T2, due to the small b-value produced by the selective AFP pulses alone. To increase diffusion weighting, a further increase in phase dispersion could be realized by using trains of AFP pulses in which individual pulses alternate frequency sweep (AFS) direction in the presence of spatial encoding gradients.
In the current study, a pair of pulsed gradients was incorporated into the LASER pulse sequence to increase the associated b-value. To date, no experimental results have been reported using selective adiabatic pulses to enhance diffusion weighting. The purpose of this study was to determine whether selective adiabatic pulse trains could produce enhanced diffusion weighting and be used in combination with pulsed gradients to measure 1H2O diffusion in phantoms spanning of a wide range of T2 values. An expression for the b-value generated by the LASER sequence was derived using the Bloch-Torrey equation following the method previously described [10, 11]. A conventional pulsed gradient spin-echo (PGSE) sequence was employed as the gold standard for diffusion measurements in all phantoms.
2. b-value Calculation using the Bloch-Torrey Equation
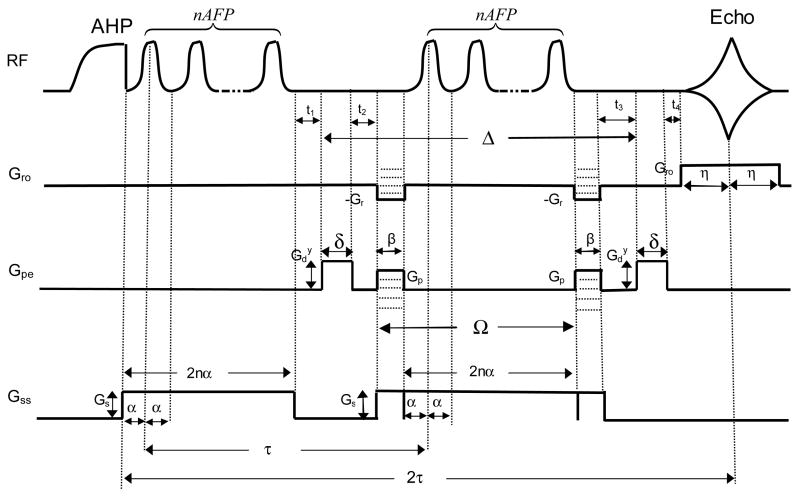
For the LASER sequence shown in Fig. 1, the Bloch-Torrey equation [12, 13] was used to describe the magnetization (M) change with time (Eq. (1)) when the self-diffusion (D) of 1H2O is considered (see Appendix for detailed parameter definitions):
Figure 1.
The LASER sequence used for diffusion weighted imaging measurements. is the pulsed gradient applied in the y-direction, Gr and Gro are frequency encoding and readout gradients, respectively, Gp is phase encoding gradient, Gs is the slice selection gradient, Δ is the diffusion time, δ is the width of , Ω is the time delay between two phase encoding gradients, α is the half-width of an AFP pulse, β is the width of Gp and Gr, t1–4, are the time delays between pulsed gradients, τ is the time interval between the first AFP pulses of the two AFP-AFS pulse trains, n is the number of AFP pulses contained in a pulse train, and η is the half-width of the readout gradient (Gro).
| (1) |
Although the full derivation of the associated b-value is described in Appendix, the assumptions made are briefly outlined. First to simplify the calculations, the effective magnetic field in the slice selective direction was expressed as the linear combination of the static magnetic field and the local gradient field [12, 13]. Second, to model the effect of an AFP pulse on the time-dependent magnetization, the nonlinear phase dispersion across a slice generated by the HS (HS1, R10) pulse [3] was expressed as a quadratic phase offset [6, 7] to the linear phase dispersion. The derived total b-value contained a cross-term from the interaction between the pulsed diffusion gradients applied in the phase encoding direction and the phase encoding gradients.
For the LASER sequence shown in Fig. 1, the derived average diffusion weighting is as follows,
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where A(2τ) is the echo amplitude, A(0) is the magnetization amplitude immediately following the adiabatic half passage (AHP) pulse, bx, by, and b̄z are the b-values in the frequency encoding, phase encoding, and slice selection directions, respectively, is the b-value cross-term in the y-direction, D is the apparent diffusion coefficient, γ is the gyromagnetic ratio, is the pulsed gradient amplitude for diffusion weighting applied in the phase encoding direction (i.e., y-direction), Gr, Gro, Gp, and Gs are pulsed gradient amplitudes for frequency encoding, readout, phase encoding, and slice selection, respectively, Δ is the diffusion time, δ is the width of , Ω is the time delay between two frequency encoding gradients (Gr), which is also the time delay between two phase encoding gradients (Gp), α is the half-width of the AFP pulse, β is the width of Gr, which is also the width of Gp and the width of crusher gradients on both sides of the slice selection gradient (Gs), τ is the time delay between the two AFP pulse trains, n is the number of AFP pulses contained in the pulse train, η is the half-width of the readout gradient (Gro), and b is the total b-value.
The b-value for the PGSE sequence was calculated using the Stejskal-Tanner equation [10, 11] with the b-value cross-term between the diffusion gradient ( ) applied in the frequency encoding direction (i.e., x-direction) and the readout gradient (Gro) included.
| (8) |
| (9) |
where 2η is the readout gradient length, and is b-value cross-term, other parameters have defined after Eq.(7).
3. Experimental
Selective adiabatic pulse trains were used in the LASER sequence (Fig. 1). Pulse trains consisted of 1, 3, 5, or 7 hyperbolic secant (HS1, R10, (3)) AFP pulses, alternating the frequency sweep direction in each subsequent pulse to increase the cumulative phase dispersion. The pulse width for a single AFP pulse was 2.5 ms. The AFP pulse was calibrated for each experiment to assure sufficient power was used to achieve the adiabatic condition. For the AFP pulse used in the experiments, ω1max/2π ≈ 1.75 kHz for A/2π = 2000 Hz and Tp = 2.5 ms, where A is the amplitude of the frequency modulation, and Tp is the pulse width.
Pulsed gradients ( ) were added symmetrically on both sides of the refocusing selective adiabatic pulse train in the phase encoding direction (y-direction) for diffusion weighting separated by a diffusion time (Δ) (Fig. 1). The average amplitudes of frequency encoding, readout, and phase encoding gradients Gr, Gro, and Gp in the LASER sequence were −3.04 G/cm, 1.22 G/cm, and 3.61 G/cm, respectively. The corresponding widths of Gr, Gro, and Gp were β = 3.6 ms, 2η = 2 ms, and β = 3.6 ms, respectively (Fig. 1). The crusher gradients on both sides of the slice selection gradient (Gs) were 3.6 ms (Fig. 1). Six phantoms (Ph-1 to Ph-6) were studied on a 4T Varian whole body MRI with a Siemens Sonata gradient coil using a hybrid birdcage transmit/receive radio frequency coil (7.7 cm ID). Phantoms consisted of 2.8 cm diameter (50 ml) plastic tubes containing a mixture of 10 μm ORGASOL polymer beads and 2 mM Gd-DTPA dissolved in 5% agar (Ph-1), and nickel(II) ammonium sulphate hexahydrate doped (56.3–0.8 mM) water solutions (Ph-2 to Ph-6). The longitudinal relaxation time constant T1 was measured from a single 5 mm transverse slice in each phantom using a fast low angle shot (FLASH) sequence (TR = 4 s, TE=3.5 ms) preceded by an AFP inversion pulse (20 inversion times (TI) ranging from 0.01–0.8 s for Ph-1 and TI ranging from 0.01–6.0 s for Ph-2 to Ph-6). The transverse relaxation time constant T2 was measured from a single 5 mm transverse slice in each phantom using a spin-echo (SE) sequence (TE = 40 – 60 ms in steps of 5 ms). The repetition time (TR) was varied (2 – 4 s) for each phantom to minimize T1 saturation.
The diffusion coefficient (D) of each phantom was measured with a conventional PGSE sequence with the pulsed diffusion gradients ( ) applied in the frequency encoding direction (x-direction) (FOV = 4 cm, matrix size = 64 × 64, in step of 0.5 G/cm, Gro = 1.27 G/cm, 2η = 2.95 ms, TE = 62 – 72 ms, TR = 2 – 4 s, δ = 10 ms, Δ = 35 – 40 ms, slice thickness = 5 mm) as the gold standard. The 90° excitation and the 180° refocusing RF pulses used in the PGSE sequence are sinc pulses of 4 ms pulse width at the calibrated powers. To measure D with the LASER sequence (Gs = 1.876 G/cm, δ = 10 ms, Δ = 35 – 40 ms, Ω = 6.1 – 21.1 ms, FOV = 4 cm, matrix size = 64 × 64, slice thickness = 5 mm) shown in Fig 1, was varied (0 – 3.5 G/cm in step of 0.5 G/cm) while fixing Δ and TE for a particular phantom. Some sequence parameters (TR = 2 – 4 s, TE = 62 – 72 ms, Δ = 35 – 40 ms, Ω = 6.1 – 21.1 ms, τ = 31 – 36 ms) were varied between phantoms with different T2 to maximize image signal to noise ratio. These parameters were the same for both PGSE and LASER sequences.
The effect of the number of AFP pulses (n) on the diffusion coefficient (D) measurement was also determined. The number of pulses (n) in the AFP-AFS pulse train was varied (n = 1, 3, 5, and 7 AFP pulses of alternated frequency sweep direction) in an effort to increase the nonlinear phase dispersion generated and thus enhance diffusion sensitivity (image contrast). For each phantom, the minimum TE for the nAFP-AFS-LASER sequence was chosen to be less than five times the T2 for that phantom. Two phantoms (Ph-1 and Ph-4) were measured using 1, 3, 5, and 7 AFP pulses in the AFP-AFS pulse train, while other phantoms were measured with n = 1 and 5 only.
T1 time constants were calculated by non-linear regression of image signal intensity (SI) with TI using the standard inversion-recovery equation. T2 time constants were calculated from the linear regression of the natural logarithm (ln) of the image SI of the SE images with TE. The D-value for each phantom was calculated by the linear regression of ln(SI) (PGSE or LASER image signal intensity) with the b-value, following correction of the image signal intensity for T2 signal loss using the T2 time constants measured for each phantom. The b-values for the PGSE and LASER sequences were calculated using Eqs. (7) and (8), respectively. The b-value terms that were independent of in Eq. (7) were constants in the varying diffusion measurements. Therefore such terms cancel out and can be ignored in the D-value calculation.
4. Results
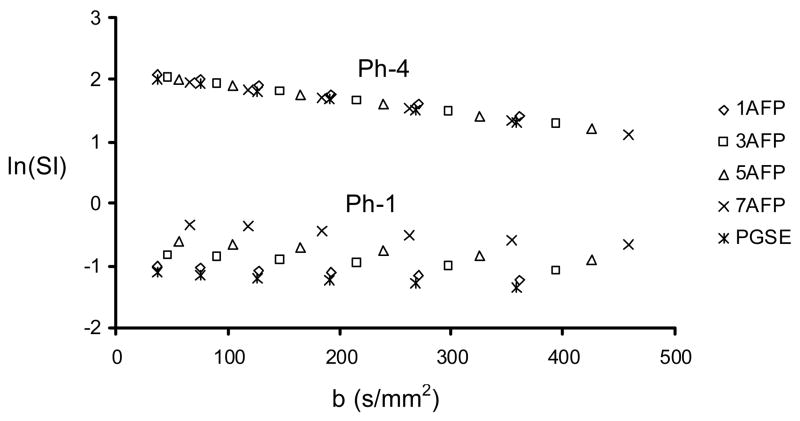
Typical diffusion weighted images are shown in Fig. 2. Increased image intensity was observed in the bead phantom (Ph-1) while decreased image intensity was observed in the nickel(II) doped water phantom (Ph-4) as the number of pulses in the AFP-AFS pulse train increased (while maintaining a constant TE). Figure 3 shows the ln(SI) as a function of b-value for Ph-1 (bottom points) and Ph-4 (top points). In the bead phantom (Ph-1), there is a clear increase in signal intensity associated with the use of more refocusing pulses in the AFP-AFS pulse train (i.e. 7 AFP line is above the 1 AFP line), while the converse is true for Ph-4. These results are in agreement with the results displayed in Figure 2. The linear regression of these curves was used to calculate the diffusion coefficients listed in Table 1.
Figure 2.
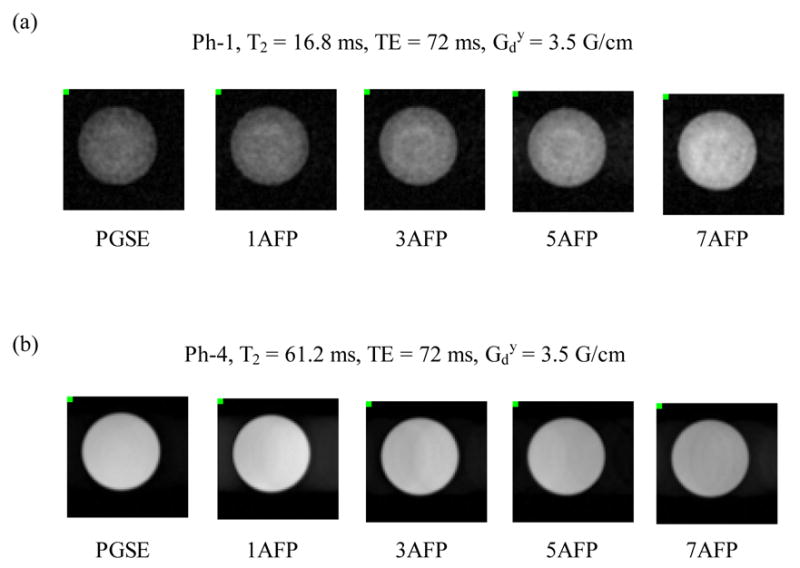
Sample images acquired using the PGSE and nAFP-AFS-LASER sequences with n = 1, 3, 5, and 7 for (a) Ph-1, the bead phantom, and (b) Ph-4, the nickel(II) doped water phantom. Echo-time (TE) and are constant for each series of images. The non-uniform image signal intensity in Ph-1 is due to the heterogeneous bead-packed materials in the phantom.
Table 1.
The measured D-coefficients, T1 and T2 time constantsa
| Phantomb | T1(ms) | T2(ms) | PGSE | 1AFP | 3AFP | 5AFP | 7AFP |
|---|---|---|---|---|---|---|---|
| Ph-1 | 36.1±1.1 | 16.7±0.2 | 0.68±0.03 | 0.70±0.02 | 0.73±0.02 | 0.78±0.02 | 0.87±0.02c |
| Ph-2 | 22.8±0.8 | 21.2±0.1 | 2.02±0.01 | 2.01±0.01 | 2.04±0.01 | ||
| Ph-3 | 54.6±1.3 | 43.3±0.1 | 2.08±0.01 | 2.04±0.01 | 2.17±0.02 | ||
| Ph-4 | 80.3±1.5 | 61.2±0.4 | 2.11±0.01 | 2.10±0.02 | 2.12±0.01 | 2.12±0.01 | 2.10±0.00 |
| Ph-5 | 188.6±1.6 | 131.1±0.7 | 2.16±0.01 | 2.10±0.00 | 2.12±0.02 | ||
| Ph-6 | 934.6±9.6 | 555.6±3.1 | 2.08±0.01 | 2.02±0.01 | 2.10±0.02 |
D-coefficients are in units of (10−3 mm2/s), and cross-terms were applied for the D-coefficient calculations of PGSE and LASER sequences, respectively; the error represents the average standard deviation of two or three repeated measurements.
Phantoms were measured using the nAFP-AFS-LASER sequence, where n = 1, 3, 5, and 7 for Ph-1 and Ph-4, and n = 1, 5 for Ph-2, Ph-3, Ph-5, and Ph-6.
Significantly different from the PGSE (ttest, p < 0.05).
The T1 and T2 time constants, and D-coefficients measured for each phantom using the standard inversion-recovery (IR), SE, and PGSE sequences, respectively, are summarized in Table 1. The D-coefficients measured using the nAFP-AFS-LASER sequences are also listed in Table 1 when using the b-value described in Equation (7). The diffusion coefficients measured by the nAFP-AFS-LASER sequence are in agreement with those measured independently by PGSE. Table 2 shows the diffusion coefficients for PGSE and nAFP-AFS-LASER sequences when and cross-terms were not incorporated in the respective b-value calculation. Notable discrepancies are observed for nearly all nAFP-AFS-LASER acquisitions compared to PGSE (Table 2).
Table 2.
D-coefficients calculated without the cross-term correctiona
| Phantomb | PGSE | 1AFP | 3AFP | 5AFP | 7AFP |
|---|---|---|---|---|---|
| Ph-1 | 0.75±0.04 | 0.74±0.01 | 0.86±0.03 | 0.98±0.03c | 1.15±0.04c |
| Ph-2 | 2.24±0.03 | 2.27±0.04 | 2.75±0.10c | ||
| Ph-3 | 2.32±0.02 | 2.31±0.04 | 2.93±0.10c | ||
| Ph-4 | 2.30±0.02 | 2.30±0.02 | 2.48±0.03c | 2.65±0.06c | 2.78±0.06c |
| Ph-5 | 2.40±0.04 | 2.38±0.04 | 2.86±0.10c | ||
| Ph-6 | 2.28±0.02 | 2.23±0.03 | 2.70±0.08c |
D-coefficients are in units of (10−3 mm2/s), and cross-terms were not applied for the D-coefficient calculations of PGSE and LASER sequences, respectively; the error represents the average standard deviation of two to three repeated measurements.
Phantoms were measured using the nAFP-AFS-LASER sequence, where n = 1, 3, 5, and 7 for Ph-1 and Ph-4, and n = 1, 5 for Ph-2, Ph-3, Ph-5, and Ph-6.
Significantly different from the PGSE (ttest, p < 0.05).
5. Discussion
A diffusion-weighted imaging sequence incorporating localization by adiabatic selective refocusing (LASER) was successfully implemented and used to measure the apparent diffusion coefficient in phantoms exhibiting a wide range of T2 relaxation time constants. In comparison to the conventional PGSE sequence, the diffusion-weighted LASER sequence can generate unique diffusion contrast at the same pulsed gradient amplitude and TE due to the enhanced nonlinear phase dispersion and the spin refocusing effect associated with the AFP-AFS pulse train. The Bloch-Torrey equations were used to derive an expression for the associated b-value for this sequence, which included a cross-term due to the interaction between the diffusion pulsed gradient ( ) and the phase encoding gradient (Gp). Including the cross-term in the b-value evaluation to account for such interaction was essential for accurate diffusion measurements.
The AFP-AFS LASER sequence produced images with increasing signal intensity in Ph-1 and decreasing signal intensity in Ph-2 (Fig. 2) as the number of pulses (n) in the AFP-AFS pulse train increased (while maintaining a constant echo-time). These results suggest that different relaxation mechanisms dominate the observed signal for each type of phantoms. In Ph-1, local field variations induced by microscopic magnetic susceptibility differences between the polystyrene beads and the surrounding Gadolinium-agarose mixture are notable; in addition, the diffusion coefficient (D) is smaller than those of the Ni(II) doped solution phantoms (Table 1). Therefore, image signal intensity was dominated by the loss of phase coherence induced by the microscopic magnetic field gradients. In the series of images shown in Fig. 2a, the dephasing induced by the microscopic magnetic field gradients was more effectively refocused as the AFP-AFS pulse train length increased, resulting in an increase in image signal intensity. The enhanced spin-refocusing effect demonstrated by the AFP-AFS pulse train is ascribed to the greater contribution of R2ρ (the transverse relaxation rate in the rotating frame during the execution of AFP pulses, R2ρ ≤ R2, where R2 is the transverse relaxation rate during the free precession of the spins) to the apparent relaxation rate (R2†) as the AFP-AFS pulse train length increased [14, 15]. That is, the apparent transverse relaxation rate (R2†) decreased as the number of AFP pulses (n) increased in the pulse train, resulting in greater echo amplitude.
For solution phantoms, such as Ph-4, the magnetic susceptibility was homogeneous within the phantom. Therefore image signal loss due to diffusion was dominated by the macroscopic phase dispersion generated by the pulsed gradients and the AFS-AFP pulse trains. In the series of images shown in Fig 2b, the macroscopic phase dispersion increased as the pulse train length increased (Eq. (A21)), resulting in a decrease in image signal intensity. T1 saturation can be ruled out as a confounding factor due to sufficiently long TR values relative to the T1 time constants for all phantoms. The experimental results (Figs 2 and 3) suggest that the contribution of R2ρ to the R2† of the nickel(II) doped phantoms was less significant than that for the bead phantom, possibly due to the difference in the microscopic magnetic susceptibility gradients within the two kinds of phantoms.
Figure 3.
ln(SI) as a function of b-value for Ph-1 and Ph-4 measured by PGSE and nAFP-AFS-LASER sequences with n = 1, 3, 5, and 7.
6. Conclusions
The nAFP-AFS-LASER pulse sequence can be used to measure apparent self diffusion with an accuracy that is comparable to that of the conventional PGSE sequence for a wide range of T2 time constants and diffusion rates. However the b-value cross-term must be incorporated in the evaluation to account for the phase encoding gradients contribution to diffusion weighting. The AFP-AFS-LASER sequence has demonstrated opposite effects on image signal intensity depending on the microscopic susceptibility characteristics and the magnitude of the diffusion coefficients. Therefore, this sequence could be beneficial for susceptibility based contrast enhancement. This important feature of the nAFP-AFS-LASER sequence in comparison to the conventional PGSE sequence may be used to identify the presence of magnetic perturbers that have different magnetic susceptibility compared to surrounding material (i.e. tissue). Superparamagnetic nanoparticles (SNPs) [16] are a particular class of magnetic perturber that generate significant local magnetic susceptibility gradients in tissue or cells. The nAFP-AFS-LASER sequence may reveal not only the distribution of SNPs but also the anatomical structure of the tissue or cells of interest by producing positive susceptibility contrast.
Supplementary Material
Acknowledgments
This work was supported by the National Institute of Health (Grant R01-EB001852), the Canadian Institutes of Health Research Multi-user Maintenance Grant (MME 15594), and the Ivey-BMO Financial Group Scientist in Brain Disorders Imaging Award. The authors also wish to thank Drs. George Caia and Amir Abduljalil for helpful discussions.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Silver MS, Joseph RI, Hoult DI. Highly selective π/2 and π pulse generation. J Magn Reson. 1984;59:347–351. [Google Scholar]
- 2.Kupce E, Freeman R. Optimized adiabatic pulses for wideband spin inversion. J Magn Reson A. 1996;118:299–303. [Google Scholar]
- 3.Garwood M, DelaBarre L. The return of the frequency sweep: designing adiabatic pulses for contemporary NMR. J Magn Reson. 2001;153:155–157. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
- 4.Conolly S, Glover G, Nishimura D, Macovski A. A reduced power selective adiabatic spin-echo pulse sequence. Magn Reson Med. 1991;18:28–38. doi: 10.1002/mrm.1910180105. [DOI] [PubMed] [Google Scholar]
- 5.Bartha R, Michaeli S, Merkle H, Adriany G, Anderson P, Chen W, Ugurbil K, Garwood M. In vivo H2O T2† measurement in the human occipital at 4T and 7T by Carr-Purcell MRI: detection of microscopic susceptibility contrast. Magn Reson Med. 2002;47:742–750. doi: 10.1002/mrm.10112. [DOI] [PubMed] [Google Scholar]
- 6.Park JY, DelaBarre L, Garwood M. Improved gradient-echo 3D magnetic resonance imaging using pseudo-echoes created by frequency-swept pulses. Magn Reson Med. 2006;55:848–857. doi: 10.1002/mrm.20821. [DOI] [PubMed] [Google Scholar]
- 7.Park JY, Grohn OHJ, Garwood M. Improved 3D spin-echo imaging using frequency-swept pulses. Proceedings of the 14th Annual Meeting of ISMRM; Seattle, WA, USA. 2006. [Google Scholar]
- 8.Kunz D. Use of frequency-modulated radiofrequency pulses in MR imaging experiments. Magn Reson Med. 1986;3:377–384. doi: 10.1002/mrm.1910030303. [DOI] [PubMed] [Google Scholar]
- 9.Sun Z, Bartha R. Can adiabatic slice selection generates diffusion weighting?. Proceedings of the 13th Annual Meeting of ISMRM; Miami Beach, FL, USA. 2005. [Google Scholar]
- 10.Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys. 1965;42:288–292. [Google Scholar]
- 11.Zu D. Magnetic resonance imaging. Higher Education Press; Beijing: 2004. [Google Scholar]
- 12.Torrey HC. Bloch equations with diffusion terms. Phys Rev. 1956;104:563–565. [Google Scholar]
- 13.Abragam A. The principles of nuclear magnetic magnetism. Oxford University; New York: 1961. [Google Scholar]
- 14.Michaeli S, Grohn H, Grohn O, Sorce DJ, Kauppinen R, Springer CS, Jr, Ugurbil K, Garwood M. Exchange-influenced T2ρ contrast in human brain images measured with adiabatic radio frequency pulses. Magn Reson Med. 2005;53:823–829. doi: 10.1002/mrm.20428. [DOI] [PubMed] [Google Scholar]
- 15.Nikolova S, Bowen CV, Bartha R. Experimental validation of a T2rho transverse relaxation model using LASER and CPMG acquisitions. J Magn Reson. 2006;181:35–44. doi: 10.1016/j.jmr.2006.03.013. [DOI] [PubMed] [Google Scholar]
- 16.Bulte JWM, Kraitchman DL. Iron oxide MR contrast agents for molecular and cellular imaging. NMR Biomed. 2004;17:484–499. doi: 10.1002/nbm.924. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.