Fig. 4.
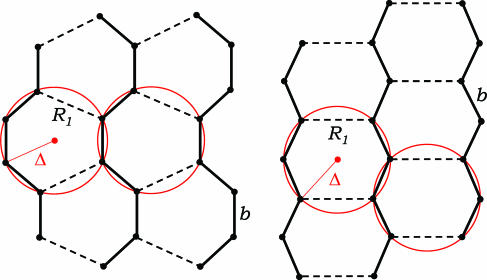
Sketch of optimally packed short segments of three tubes (solid lines) obtained from metropolis Monte Carlo annealing simulations at the edge of compaction. The self-avoidance of a discrete tube [defined through a set of N points along the discretized tube axis {r1, r2, …, rN} with unit spacing (b = 1) between consecutive points] is enforced through the three-body potential defined in the legend of Fig. 1. The number of pairwise contacts between nonconsecutive beads is maximized. Any two such beads are forbidden to come closer than 1.1 units and are defined to form a contact when they come closer than 1.6 units (R1 = 1.6) (these numbers have been selected to conform to the known length scales associated with real proteins). For convenience, the three tube segments are placed inside a hard-wall spherical box of radius 9 units—the conformations shown are not affected by the presence of the walls. Our simulations were performed with standard pivot, crank-shaft, and tail slithering move sets. Random translations of one of the chains were also attempted. All tubes have a radius Δ = 1.1. To minimize edge effects, the tubes were of different lengths, and the first and last points, which are not shown in the figure, were not allowed to form any contact. One obtains eight pairwise contacts for both of the ground state arrangements shown in the figure as dashed lines. Also drawn, in red, are some of the circles of radius Δ going through several local and nonlocal triplets.