Quantitative structure-permeation relationship for iontophoretic transport across the skin

Abstract

The objective was to relate the efficiency of a charged drug to carry current across the skin during iontophoresis to its structural and/or physicochemical properties. The corollary was the establishment of a predictive relationship useful to predict the feasibility of iontophoretic drug delivery, and for the selection and optimization of drug candidates for this route of administration. A dataset of 16 cations, for which iontophoretic fluxes have been measured under identical conditions, with no competition from exogenous co-ions, was compiled. Maximum transport numbers correlated with ion mobilities and decreased with ionic size, the dependence indicating that the electromigration mechanism of iontophoresis would become negligible for drugs of hydrodynamic radius greater than about 8Å. Validation of the model was demonstrated by successfully predicting the transport numbers of three structurally distinct dipeptides, the iontophoretic data for which had been determined under distinctly different experimental conditions. Finally, for the “training” set of cations, a strong linear dependence between their transport numbers in skin and those in aqueous solution was demonstrated; the former were larger by approximately a factor of 1.4 consistent with skin’s cation permselectivity. In conclusion, this research offers a practical contribution to the development of a predictive structure-transport model of iontophoresis.

Introduction

Iontophoresis is a technique that uses a mild electric current (0.5 mA/cm²) to drive charged substances across the skin [1,2]. The approach has been used for drug delivery and, in “reverse” mode, for clinical monitoring [1–3]. The principal mechanism of transport during iontophoresis is electromigration: the result of the direct interaction of the electric field with the ion of interest. In this case, the transdermal flux of ion “i” (J_i) is linked to the intensity of current applied (I) via Faraday’s law [4]:

$$J_i=\frac{t_i·I}{z_i·F}$$ (eq.1)

where t_i and z_i are the transport number and the valence, respectively, and F is Faraday’s constant. The transport number is defined as the fraction of the total charge transported by a specific ion during iontophoresis and is related to its effectiveness as a charge carrier, and to the presence of competitor co- and counter-ions and their corresponding charge-carrying abilities [1–4].

It is anticipated that the efficiency of an ion as a charge carrier will decrease with molecular weight, a hypothesis supported by experimental observations [5–10]. While this would seem to imply that iontophoresis would ultimately have no impact on large ions, a second mechanism of transport – namely, electroosmosis - assumes a dominant, although quantitatively smaller, role for cationic species [11]. Electroosmosis is a convective solvent flow in the anode-to-cathode direction induced by the fact that skin has a net negative charge under physiological conditions [12,13]. This phenomenon therefore leads to increased movement of neutral, polar substances (which have very low passive skin permeabilities) and supplements the electrotransport of cations [14–16]. While electroosmotic transport is less efficient than electromigration [15,17], it becomes progressively more important for larger cations, the transport numbers of which diminish eventually to very low values [11,18].

In vivo, the ubiquitous presence of endogenous ions at high concentration beneath the skin barrier means that the efficiency of iontophoretic drug transport by electromigration is limited to a maximum value which is significantly less than 100%. This maximum transport number (t_oC+) can be measured in so-called “single-ion” or “single-carrier” experiments, in which the drug is the only ion available for carrying the charge into the skin [19–23]. In this situation, competition comes only from counter-ions beneath the skin, principally chloride ions for a cationic drug, sodium ions for an anionic species. Thus, measurement of t_oC+ (using chloride as a counter-ion) constitutes the most straightforward procedure to test the feasibility of iontophoretic delivery of a cationic drug.

However, transport numbers in the single-ion situation (t_oC+) are seldom reported. Instead, the literature contains transport numbers which have been determined under a wide variety of experimental conditions, using electrodes and formulations comprising diverse background electrolytes and buffers. This is the case even in certain investigations which have attempted to identify the influence of molecular properties (such as molecular weight, logP, specific conductivity) on iontophoretic transport [5–10, 24–26]. That such studies have not been able to fully reveal fundamental patterns of behaviour can be explained by the significant presence of competing co- and counter-ions, which greatly affect the transport number of the drug of interest; the latter, under these circumstances, is no longer an intrinsic property of the ion itself. In contrast, drug delivery in the single-ion situation is primarily determined by the relative diffusivities of the drug and the principal counter-ion (chloride), and is independent of concentration. Thus, this is a much better parameter with which to build predictive models. The value of t_oC+ is available for only a few drugs in the 200–400 Dalton molecular weight range: lidocaine (0.16), ropinirole (0.10), hydromorphone (0.11), propranolol (0.04) and quinine (0.03) [20–23]. By comparison, small inorganic cations such as Li⁺, Na⁺, K⁺ and NH₄⁺ (6–39 Daltons), when iontophoresed as single ions, have transport numbers between 0.54 and 0.77, a range that must signify the maximum achievable for any cationic drug [27]. While these two sets of data suggest that t_oC+ (i.e., the efficiency of a cation as a charge carrier) decreases rather quickly with increasing molecular weight, the quantitative relationship between transport number and the physicochemical properties of the ion has not been characterized. The principal objective of the work described in this paper was to define this relationship, therefore. For this purpose, the transport numbers of a further series of cations (MW=74–223) in the single-ion situation were determined, and their dependence upon molecular weight, hydrodynamic radius and aqueous mobility was subsequently analyzed.

A second, important objective was to investigate further a previously suggested correlation 27 between the aqueous mobility of a cation and its transport number (again as a single-ion carrier) across the skin. Establishment of such a direct dependence would offer a potentially valuable tool with which to predict the feasibility of iontophoretic drug delivery.

Materials and Methods

1. Materials

Eight cationic halides were studied (Table 1), providing a third dataset of information to complement those from the two groups of ions already evaluated (Figure 1). Specifically: tetra-N-methylammonium chloride (TMA), tetra-N-ethylammonium chloride (TEA), tetra-N-propylammonium chloride (TPR), choline chloride (CHO), carbamoylcholine chloride (CBC) and magnesium chloride were purchased from Fluka (Saint-Quentin Fallavier, France); S-butyrylthiocholine chloride (BTC), neostigmine bromide (NEO), pyridostigmine bromide (PYR), silver chloride (99%) and silver wire (99.9%) were obtained from Sigma-Aldrich (Saint Quentin Fallavier, France). Deionized water (resistivity ≥18.2 MO cm) was used to prepare all solutions.

Table 1.

Chromatographic conditions employed for the analysis of compounds studied in this work.

N°	Compound	Detection mode a	Column b	Mobile phase c
5	Tetra-N-methylammonium Chloride	ED	CG14 + CS14	HMSA 5mM + ACN 5%
6	Tetra-N-ethylammonium Chloride	ED	CG14 + CS14	HMSA 30mM + ACN 5%
7	Tetra-N-proylammonium Chloride	ED	CG14 + CS14	HMSA 30mM + ACN 20%
8	Choline Chloride	ED	CG14 + CS14	HMSA 5mM + ACN 20%
9	Butyrylthiocholine Chloride	ED	CG14 + CS14	HMSA 30mM + ACN 20%
10	Carbamoylcholine Chloride	ED	CG14 + CS14	HMSA 5mM + ACN 20%
11	Neostigmine Bromide	UV (260nm)	Zorbax CN	[Acetate buffer pH=5.2 + HESA 10mM] 30% + ACN 70%
12	Pyridostigmine Bromide	UV (275nm)	Zorbax CN	[Acetate buffer pH=5.2+ HESA 10mM] 40% + ACN 60%

^aED = electrochemical detection; UV = ultraviolet detection.

^bCG = Column guard; CS = analytical column.

^cHMSA = Methanesulfonic acid, ACN = Acetonitrile, HESA = heptansulfonic acid sodium salt

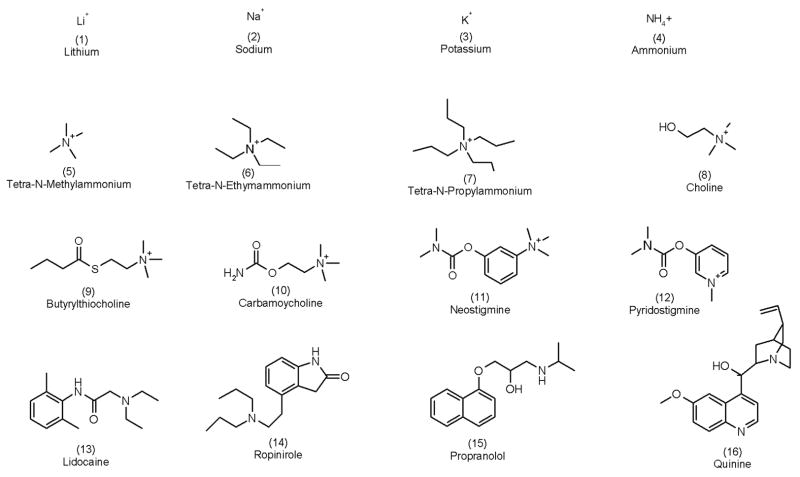
Figure 1.

The 16 cations analyzed in this work. The numbers in parentheses are used to identify the compounds in the text and in Figures 2 and 3.

2. Skin preparation

Porcine ears were obtained from the local slaughterhouse (Annecy, France) and cleaned under cold running water. Either the external or the inner ear surface was dermatomed to 750 μm with an air dermatome (Zimmer, Dover, Ohio). Pig skin is considered an excellent model for human skin in iontophoresis studies [28,29]. The pieces of skin were wrapped in Parafilm® and stored at −20°C for no longer than two months. Four to six replicates were performed for each condition using skin originating from at least four different animals.

3. Iontophoresis experiments

The skin was clamped between the two halves of side-by-side diffusion cells (transport area 0.78 cm²) with the stratum corneum facing the anodal chamber. Both the donor and the receptor chambers were filled with deionized water during two equilibrating periods of 30 minutes to verify that the cells were sealed correctly with no leaks. Subsequently, the cathodal compartment was filled with 3 mL of 5 mM MgCl₂ solution. This solution was chosen to provide a source of chloride, which is the principal endogenous counterion limiting iontophoretic cation delivery. The anodal chamber was filled (1.5 mL) with a 10 mM aqueous solution of the respective chloride or bromide salt of the cation. The pH of the unbuffered anodal solutions fell between 5 and 6; addition of very small amounts of 10 mM HCl was used to normalize all solutions to pH 5. The resulting H⁺ concentration was therefore on the order of 1/1000th of that of the cation of interest, and ensured > 99% ionization of all the cations considered. The pH of the solutions remained essentially constant throughout the experiments. To avoid depletion of the cation being delivered, the anodal chamber was continuously perfused (3 mL/h) with the donor solution via a syringe pump (Genie 8, Kent Scientific Corporation, Torrington, CT, USA).

A constant direct current (0.4 mA) was applied for 7 hrs via Ag/AgCl electrodes connected to a power supply (Kepco APH-1000DM, MB Electronique, France). In the case of neostigmine and pyridostigmine bromide salts, a silver wire was used as the anode. The entire cathodal solution was sampled every hour and the electrode chamber refilled with fresh MgCl₂ solution.

4. Sample analysis

Six of the eight compounds studied (Nos. 5–10; Figure 1) were assayed by ion chromatography (Dionex 600, Dionex, Sunnyvale, CA) equipped with a gradient pump (GP-50), a thermal compartment (AS-50), and an electrochemical detector (ED-50). Quantification was performed in the suppressed conductivity mode; the electric current applied to the suppressor was 50 mA. The regeneration of the suppressor was assured by an external supply of deionized water. The flow rate was fixed at 1 mL/min. Specific details for the analysis of each compound are shown in Table 1.

Neostigmine and pyridostigmine bromides (compounds 11 and 12; Figure 1) were assayed by HPLC-UV (Waters 600^(™) Controller, 486 Tunable Absorbance Detector, and a 717 autosampler, Waters Corporation, MA). The flow rate of the mobile phase was 1 mL/min. Other details of the analyses are specified in Table 1.

5. Data sets

The transport numbers of Li⁺, Na⁺, K⁺ and NH₄⁺ as single-ions have been published elsewhere [27]. Briefly: Ag/AgCl electrodes were used to deliver 0.4 mA across porcine ear skin. The cations were incorporated as chloride salts and the cathodal solution was 5 mM MgCl₂. The transport numbers of lidocaine (pKa=8.5), propranolol (pKa=9.1), quinine (pKa=9.3) and ropinirole (pKa=9.5) hydrochlorides (compounds 12–16; Figure 1) have been previously reported [20,21,23]. Again, Ag/AgCl electrodes were used to deliver 0.4 mA across porcine skin. The cathodal solution, for these cations, was 25 mM HEPES-buffered normal saline at pH 7.4.

6. Conductivity measurements

The specific conductivity (Ohm⁻¹ cm⁻¹) of aqueous solutions of the cation halides (with the exception of propranolol hydrochloride) spanning a wide range of concentrations (50, 25, 12.5, 6.25 and 3.125 mM) was measured with a conductimeter (Metrohm 712, Herisau, Switzerland) at 25°C. The results were used to estimate aqueous mobilities as follows. The molar conductivities (? m: Ohm⁻¹ cm⁻¹ mol⁻¹) (the specific conductivity normalized by the concentration) were plotted as a function of the square root of the concentration [30], and extrapolation to zero concentration allowed the molar ionic conductivity at infinite dilution for each salt (? °m; ohm⁻¹ cm⁻¹ mol⁻¹) to be estimated. The regression lines “molar conductivity as a function of the square root of the molar concentration” were linear, with r² values > 0.9 in all cases. The molar conductivity of the ion of interest was then obtained by application of Kohlrausch’s law of independent migration of ions [28], and the mobility (u: cm² s⁻¹ V⁻¹) was calculated by dividing the molar ionic conductivity by Faraday’s constant. For example, the molar conductivity of lidocaine as a function of the square root of the molar concentration (M) resulted in a straight line: ? m (Ohm⁻¹ cm⁻¹ mol⁻¹)= −115.7√M + 99 (r² = 0.9969), thus ? °m for LHCl salt was 99 ohm⁻¹ cm⁻¹ mol^−1. By substracting the contribution of chloride (76.3 ohm⁻¹ cm⁻¹ mol⁻¹ [30]), the molar conductivity of LH⁺ was obtained (22.7 ohm⁻¹ cm⁻¹ mol⁻¹⁾. LH⁺ mobility was 22.7/96500=2.3×10⁻⁴ cm² s⁻¹ V⁻¹). Finally, the hydrodynamic radius (a) was obtained via the Einstein relation (D=uRT/zF) and the Stokes-Einstein equation (D=kT/6Πηa) [30]. The mobility of propranolol, measured using capillary zone electrophoresis (CZE), has been recently published [31].

7. Transport numbers

Cationic transport numbers were calculated at the 6th hour of iontophoresis using equation 1 and are reported as the mean and standard deviation. The 6-hour iontophoretic fluxes of all the cations considered had reached steady-state by this time. Because of the contribution of electroosmosis to the total flux, the term transference number (which quantifies the moles of substance transported per mol of electrons independent of the mechanism of transport) would be more appropriate [32]. However, as transport number is the term typically employed in transdermal iontophoresis, its use has been maintained to describe the transport efficiency of the ion of interest.

Transport numbers in aqueous solution were estimated for each cation/halide pair via equation 2 [30]

$${\text{t}}_{\text{C}+}={\text{u}}_{\text{C}+}/({\text{u}}_{\text{C}+}+{\text{u}}_{{\text{Cl}}^{-}})$$ (eq.2)

where u_C+ and u_Cl⁻ are the mobilities of the cation and anion, respectively.

8. Statistical analysis

Non-linear and linear regressions, and correlation analysis of the data, used Prism 4 (GraphPad Inc. Software, San Diego USA). Linear regressions were followed by the corresponding ANOVAs to test the level of significance. The Pearson correlation test was used to evaluate the significance of the relationship between ionic transport numbers across the skin during iontophoresis and those in water [33]. The correlation coefficient (r) measures the intensity of association between two variables, and varies between zero (no association) and 1. The coefficient of determination (r²) was used as a measure of the strength of the regression line; briefly, it indicates the proportion of the total variation in the Y variable (cation transport number in the skin) that is accounted for by correlating it with the second variable (transport numbers in water). All correlations and regressions discussed in the text were significant at p < 0.05.

Results and discussion

A first objective of this work was to relate the physicochemical properties of a cation to its transport number in the single-ion situation. Molecular weight has been identified as an important determinant of iontophoretic flux in the presence of competing co- and counter-ions, and a distinct inverse relationship has been observed 5–10. In contrast with previous work, attention has been focused here on cation transport numbers measured in the single-carrier situation; in this case, only the diffusivities of the cation and the counter-ion determine the transport number [19]. All data were taken from experiments in which chloride, the principal endogenous counter-ions, was used. Thus, as the diffusivity of the counter-ion was kept constant, the value of t_oC+ depended solely on the intrinsic properties of the cation. Further, because Cl⁻ is the ubiquitous counter-ion in vivo, the results were expected to be predictive of behaviour in the “ practical world”.

Figure 2.a shows that t_oC+ decreases rapidly with molecular weight, with transport numbers approaching zero at 400–500Da. It is noted that the t_oC+ of small inorganic cations (Li⁺, Na⁺, K⁺ and NH₄⁺) were not well-correlated with their formula weights, leading us to examine more suitable molecular descriptors. In the single-ion scenario, with Cl⁻ as the counter-ion, the cation transport number may be theoretically predicted by equation 3 [19]:

Figure 2.

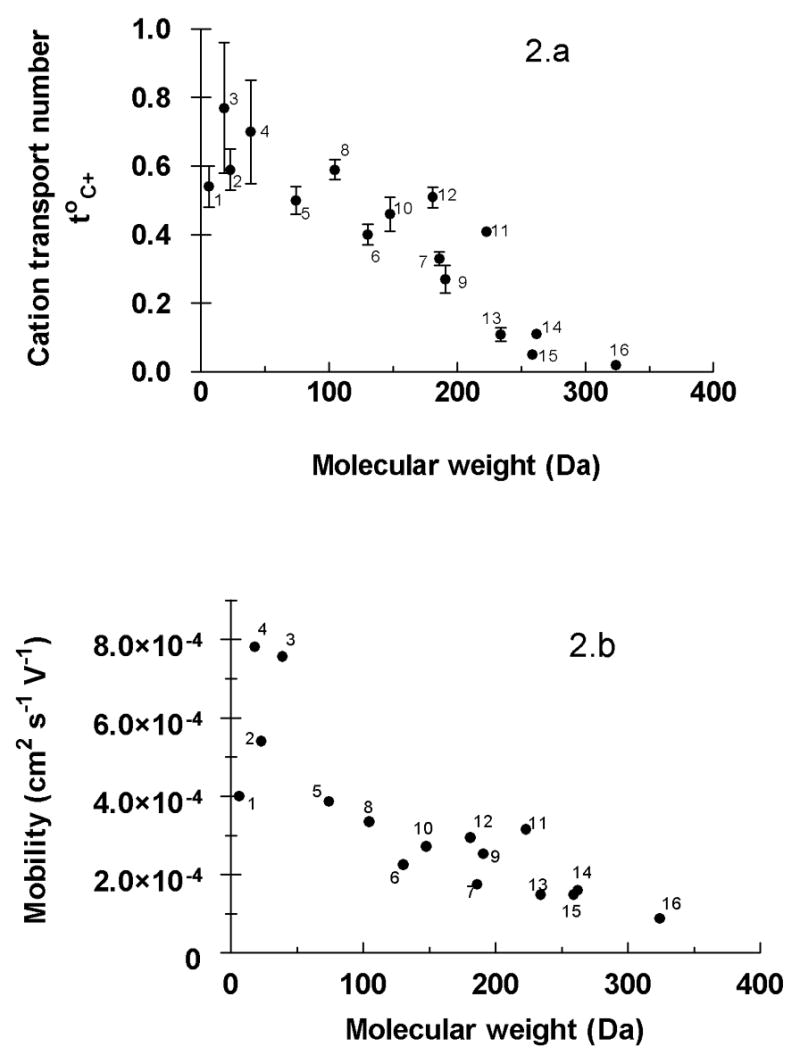
Cationic transport numbers (Figure 2.a) in the single-carrier situation and mobilities (Figure 2.b) as a function of atomic/molecular weight.

$${\text{t}}_{\text{oC}+}={\text{D}}_{\text{C}+}/({\text{D}}_{\text{C}+}+{\text{D}}_{{\text{Cl}}^{-}})$$ (eq.3)

where D_C+ and D_Cl⁻ are the diffusivities of C⁺ and Cl⁻ in the membrane, respectively. Unfortunately, these values are not easily measured. On the other hand, the Einstein relation (D=uRT/zF) links ionic mobility (u) to the diffusion coefficient [30]. The mobility of an ion describes its behaviour in a given solvent, under the influence of an electric field, and depends upon the charge and the hydrodynamic radius (i.e., the radius of the ion plus the surrounding sphere of solvent). While mobility generally decreases with molecular weight, lithium (the smallest of the cations considered here) is, in fact, a less mobile species because its hydrodynamic radius is larger – due to its considerable solvation sphere - than that of the other, small inorganic cations studied. This is clearly apparent upon inspection of Figure 2.b where ionic mobility, determined from conductivity measurements, is plotted as a function of the molecular weight.

The relationship between the cationic mobility and transport number across the skin as a single carrier was next examined (Figure 3.a). An exponential increase of the transport number with mobility towards a plateau or limiting value was observed. The physical significance of this limit is due to counter-ion (chloride) competition. It has been shown [34], that a total cationic transport number (St_oC+) of 0.65–0.85 is conserved for a series of anodal formulations containing Li⁺, Na⁺, K⁺ and NH₄⁺ over a total ionic concentration range from 125 to 200 mM. The best empirical fit to the data in Figure 3.a was the following equation:

Figure 3.

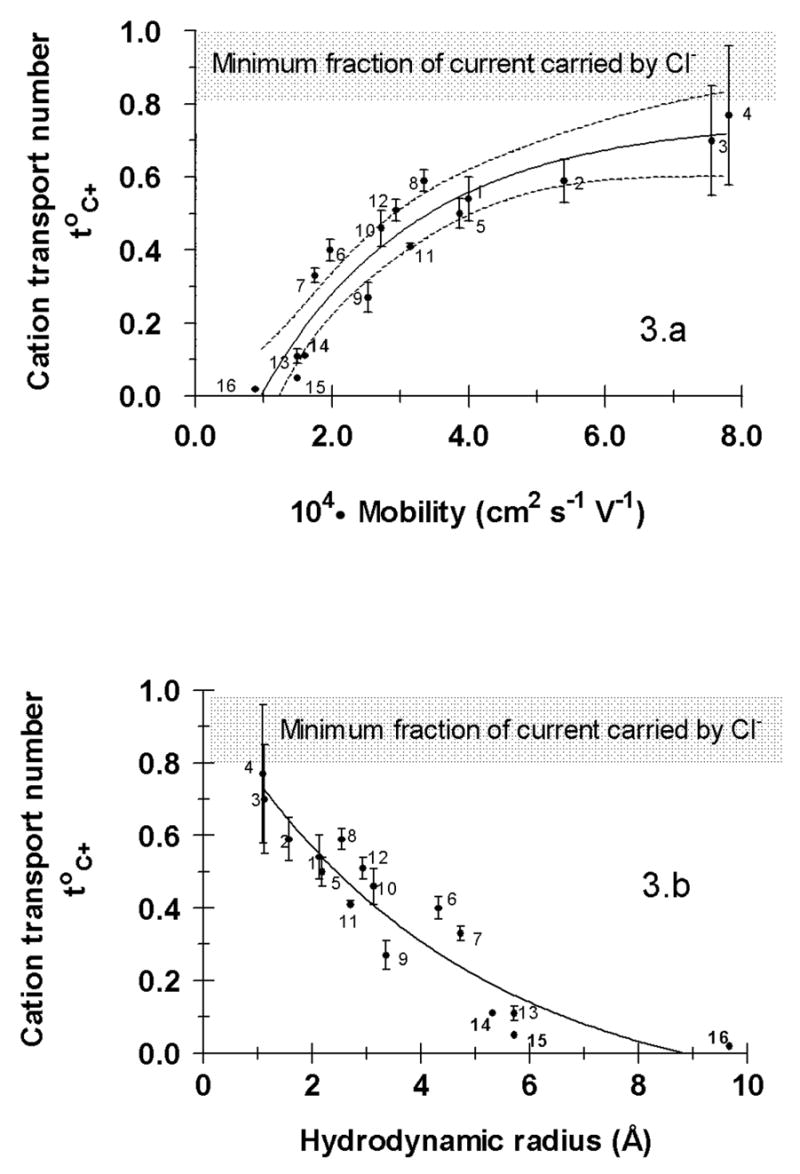
(a) The important dependence of cation transport number on mobility (u). The data were empirically fitted to the equation: t^o_C+= B + (A−B)(1−e^−kx) and the parameters (mean ± SE) estimated by non-linear regression were: B = −0.39 ± 0.17, A = 0.756 ± 0.08 and k = 4401 ± 1225 cm⁻².s.V (r²=0.887). The 95% confidence interval is indicated by the dashed lines. (b) The behaviour in the upper panel re-expressed in terms of the cation hydrodynamic radius; the smaller, more mobile ions show the highest transport numbers.

$${\text{t}}_{\text{oC}+}=-0.40+1.15\hspace{0.17em}(1-exp(-4401•\text{u}))$$ (eq.4)

with r² = 0.887. This regression predicts a limiting t_oC+ of 0.76 ± 0.08, a maximum imposed by the competition with chloride to carry current across the skin, and a value in excellent agreement with experimental data [34]. At the opposite extreme, equation 4 indicates that cations with mobilities less than 0.95.10⁻⁴ cm².s⁻¹.V⁻¹ will carry a negligible amount of current across the skin during transdermal iontophoresis (i.e., the t_oC+ for these species would be ~ 0). From the combined datasets examined, this would mean that cations having mobilities close to (or less than) that of quinine would be expected to be transported predominantly by electroosmosis, their electromigration contributions being indistinguishable from zero. However, the situation is in fact more complicated because quinine (and propranolol and, to a certain extent, ropinirole) are relatively lipophilic cations known to interact significantly with the net negative charge of the skin and to change its permselective properties [20, 21]. It is likely, therefore, that the limit on mobility may be somewhat (but not dramatically) lower than that predicted by equation 4. This hypothesis is discussed and illustrated further below.

Figure 3.b provides a different perspective on the same data and plots the transport number as a function of the hydrodynamic radius calculated using the Stokes-Einstein relation [30]. Broadly speaking, this approach suggests that t_oC+ becomes negligible for molecules whose hydrodynamic radii exceed about 8 Å. Two further points about Figure 3.b should be emphasized: First, the transport numbers of the small inorganic cations now align correctly (compare with Figure 2) as described above. Second, it is important to appreciate that this representation constitutes a simple arithmetical transformation of Figure 3.a given that the hydrodynamic radius is directly calculated from the mobility assuming that the ions are spherical [30]. For data-fitting and prediction, mobility, which is experimentally measured is therefore preferred; for illustrative purposes, on the other hand, graphical presentation as a function of hydrodynamic radius has its obvious advantages.

Further analysis of the data compared the cationic transport numbers in the skin to those in aqueous solution which were estimated from the measured mobilities via equation 2 [27]. Figure 4 shows the resulting correlation. A Pearson correlation test [33], which assesses the strength of association between the two variables, yields a correlation coefficient (Pearson r) of 0.91; that is, a strong and positive relationship. The coefficient of determination (r²) is 0.83, indicating that more than 83% of the variance in the two parameters is shared. In short, therefore, there is a strong correlation between ion transport numbers in the skin and those in aqueous solution. A subsequent linear regression analysis of the data was highly significant and yielded the following expression:

Figure 4.

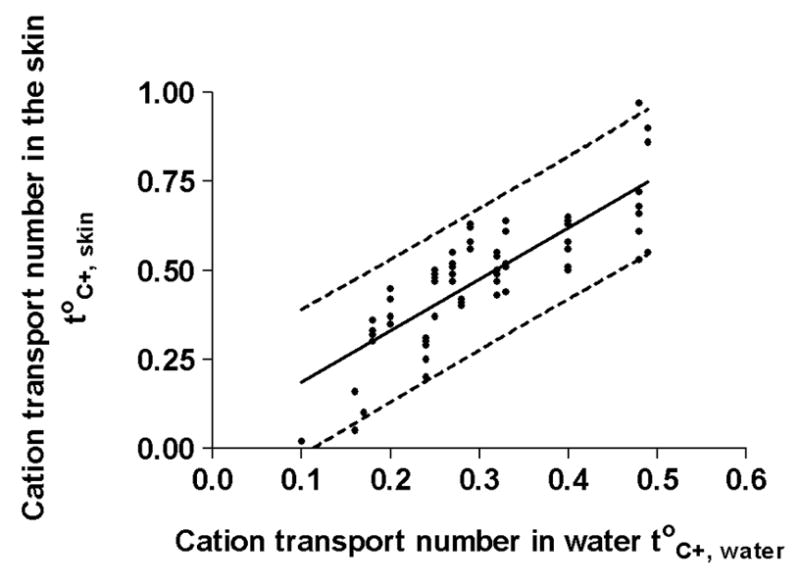
Correlation between cation transport numbers in skin with the corresponding values in water. A Pearson test shows the correlation to be strong and positive. Linear regression analysis confirms that the values in the skin are systematically higher than those in aqueous solution, a consequence of the membrane’s net negative charge and resulting cation permselectivity. The linear regression is characterized by equation 4 (see text); the dashed lines correspond to the 95% prediction interval.

$${\text{t}}_{\text{oC}+,\hspace{0.17em}\text{skin}}=1.446(\pm 0.119)\hspace{0.17em}{\text{t}}_{\text{oC}+,\hspace{0.17em}\text{water}}+0.041\hspace{0.17em}(\pm 0.037)$$ (eq.5)

with r² = 0.67. It follows that, in general, cationic transport numbers in the skin are 1.4 times those in water, a clear indication of the skin’s permselectivity. It is noticeable that the three lowest transport numbers in the skin (that is, those of ropinirole, propranolol, and quinine) are overestimated by equation 5, a finding that may be explained, at least in part, by the interaction of these drugs with the skin and their inhibition of electroosmotic flow [20,21].

Finally, it is appropriate to assess whether the structure-transport relationships developed here, and in related work [27,34], are broadly applicable, in particular to compounds from a distinctly different class. To illustrate this point, data on the iontophoretic delivery of cationic dipeptides (charge +2 at pH 7.4) [31] have been examined. In this case, mobilities were measured by capillary zone electrophoresis (CZE) and iontophoresis was not perfomed under single-carrier conditions. However, the molar fraction of each peptide in the anodal formulation was easily calculable and, using this known value (x_p+) together with the transport number (t_p+) deduced from the measured flux, it was possible to determine the peptide transport number under single-ion conditions (t_o,p+) from:

$${\text{t}}_{\text{op}+}={\text{t}}_{\text{p}+}/{\text{x}}_{\text{p}+}$$ (eq.6)

Data supporting the validity of this approach have been reported in the literature for small inorganic cations and for drugs such as lidocaine [23,28]. The cationic peptides considered here, their molecular weights and measured mobilities, their calculated t_op+ (from eq.6 and the experimentally determined t_p+ and x_p+), and the predicted values of t_op+ using equation 4 are in Table 3; comparative data for lidocaine assessed under exactly the same conditions as the peptides are also shown. The three peptides indicated were selected because their measured mobilities fell within the range of those exhibited by the cations studied in the present work. The agreement between the predictions of equation 4 and the experimentally deduced values of t_op+ is excellent, supporting the utility of the structure-transport relationships derived here and in related recent work. Furthermore, it is worth adding that the single-ion carrier transport numbers of three additional cationic peptides, whose mobilities were less than 1×10⁻⁴ cm²s⁻¹V⁻¹ (that is, outside the range of those used to develop the quantitative relationship in eq.4), were under-predicted by the model. This finding reflects two clear messages: first, that predictive equations work best only within the “boundary conditions” of the data used for their generation; and, second, that the results for the lipophilic cations identified earlier (in particular, propranolol, quinine and ropinirole) have skewed the predictions of the model to under-estimate transport numbers of larger cations which do not associate appreciably with the skin membrane. Additional work with such species having molecular weights ≥300 Daltons should clearly be undertaken to better characterize the structure-transport relationship at this limit.

Table 3.

Mobilities, and experimental and predicted “single-ion” transport numbers, of three cationic dipeptides [31] across the skin. Data for lidocaine, obtained under identical experimental conditions, are shown for comparison.

Cation	Structure	MW (Daltons)	104.Mobilitya (cm2.s−1.V−1)	t0P+ experimentalb	t0P+ predicted (eq.5)c
H-Lys-Lys-OH (KK)		274	1.67	0.20	0.20
H-Tyr-Lys-NH2 (YK-NH2)		308	1.46	0.16	0.14
H-Tyr-D-Arg-NH2 (YdR-NH2)		336	1.52	0.18	0.16
Lidocaine		234	1.38	0.11	0.12

^aExperimentally measured by capillary zone electrophoresis [31]

^bCalculated from iontophoretic flux measurements as described in the text.

^cPredicted from eq. 4 using the CZE mobilities in the Table.

Conclusion

The efficiency of iontophoretic delivery is reflected in the transport number of the ion across the skin. The maximum value of this transport number has been shown to be a sensitive function of the ion’s mobility. The limiting value of the transport number is about 0.75 for very mobile, small inorganic cations such as Na⁺ and Li⁺. The transport number falls off exponentially with decreasing mobility, such that its value is no more than 0.20 for a modestly-sized drug such as lidocaine. The empirical relationship derived, though not yet optimal, successfully predicts the efficiency of iontophoresis of structurally distinct cations, including some dipeptides. It has also been shown that cation transport numbers across the skin are highly correlated with those in aqueous solution. Taken together, therefore, the results from this work represent a useful step towards the development of a predictive model of iontophoretic transport.

Table 2.

Physicochemical properties of the cations evaluated.

Code	Cation	MW (daltons)	104.Mobility cm2.s−1.V−1	Transport number t°C+ (Mean ± SD)
1	Lithium	6	4.00	0.54 ± 0.06 a
2	Sodium	23	5.40	0.59 ± 0.06 a
3	Potassium	39	7.56	0.77 ± 0.19 a
4	Ammonium	18	7.81	0.70 ± 0.15 a
5	Tetra-N-methylammonium	74	3.90	0.50 ± 0.04
6	Tetra-N-ethylammonium	130	1.97	0.40 ± 0.04
7	Tetra-N-proylammonium	186	1.80	0.33 ± 0.02
8	Choline	104	3.35	0.59 ± 0.03
9	Butyrylthiocholine	190	2.53	0.27 ± 0.04
10	Carbamoylcholine	147	2.72	0.46 ± 0.05
11	Neostigmine	223	3.15	0.41 ± 0.01
12	Pyridostigmine	181	2.94	0.51 ± 0.03
13	Lidocaine	234	1.49	0.16 ± 0.02b
14	Ropinirole	262	1.60	0.10 ± 0.01c
15	Propranolol	259	1.49d	0.03 ± 0.01b
16	Quinine	324	0.88	0.02 ± 0.01b

^aData from [34]

^bData from [20]

^cData from [21]

^dMobility measured using capillary zone electrophoresis [31]