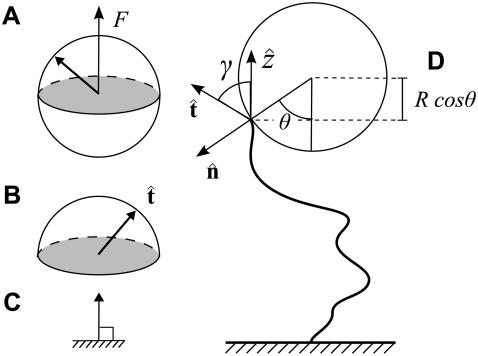
FIGURE 4.

Sketch of the boundary conditions. (A) Unconstrained boundary conditions. The tangent vector at the end of the chain (short arrow) points in any direction relative to the direction of applied force (notched arrowhead). (B) Half-constrained boundary conditions. Due to a constraint (such as the presence of a solid surface), the tangent vector at the end of the chain can point only in the upper half-sphere. (C) Perpendicular boundary conditions. The tangent vector is constrained to point only normal to the surface in the direction of the applied force. (Note that boundary conditions are necessary for both ends (s = 0 and s = L) of the chain.) (D) Variables used to describe bead rotational fluctuations. The vector 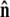points from the center of the bead to the polymer-bead attachment. The angle θ between the 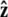direction and the bead-chain attachment is defined by 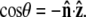The angle γ is defined by 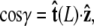where 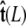is the tangent vector at the end of the chain. The bead has radius R.