Effects of Sustained Length-Dependent Activation on In Situ Cross-Bridge Dynamics in Rat Hearts

Abstract

The cellular basis of the length-dependent increases in contractile force in the beating heart has remained unclear. Our aim was to investigate whether length-dependent mediated increases in contractile force are correlated with myosin head proximity to actin filaments, and presumably the number of cross-bridges activated during a contraction. We therefore employed x-ray diffraction analyses of beat-to-beat contractions in spontaneously beating rat hearts under open-chest conditions simultaneous with recordings of left ventricle (LV) pressure-volume. Regional x-ray diffraction patterns were recorded from the anterior LV free wall under steady-state contractions and during acute volume loading (intravenous lactate Ringers infusion at 60 ml/h, <5 min duration) to determine the change in intensity ratio (I_1,0/I_1,1) and myosin interfilament spacing (d_1,0). We found no significant change in end-diastolic (ED) intensity ratio, indicating that the proportion of myosin heads in proximity to actin was unchanged by fiber stretching. Intensity ratio decreased significantly more during the isovolumetric contraction phase during volume loading than under baseline contractions. A significant systolic increase in myosin head proximity to actin filaments correlated with the maximum rate of pressure increase. Hence, a reduction in interfilament spacing at end-diastole (∼0.5 nm) during stretch increased the proportion of cross-bridges activated. Furthermore, our recordings suggest that d_1,0 expansion was inversely related to LV volume but was restricted during contraction and sarcomere shortening to values smaller than the maximum during isovolumetric relaxation. Since ventricular volume, and presumably sarcomere length, was found to be directly related to interfilament spacing, these findings support a role for interfilament spacing in modulating cross-bridge formation and force developed before shortening.

INTRODUCTION

The increase in left ventricle (LV) contractile force required to increase cardiac output after an acute increase in venous return is the basis of Frank-Starling's law of the heart. Many researchers have shown that there is a time-dependent increase in contractile force during the first minutes of volume expansion. Sustained stretch of the LV myofibers increases intracellular Ca²⁺ release when prolonged for more than a few minutes, resulting in an additive slow force response (1–3) and further enhancement of the initial force increase. Nevertheless, length-dependent activation (LDA) is the most important means of increasing contractile force that operates on a beat-to-beat basis, independent of changes in Ca²⁺ transients. Hence, this mechanism is distinct from changes in contractility (4).

Using sonomicrometry, Lew (1) has shown that across the LV free wall the initial increase in contractile force during stretch induced by volume loading results in an enhanced shortening of muscle with a gradual reduction in regional systolic LV segment length. More importantly, the enhanced shortening of muscle associated with stretch appeared to be uniform in response in the anterior, lateral, and posterior walls of the LV (1). Thus, there appears to be a high degree of correlation between regional and global function in response to stretch in the normal myocardium.

Stretch of the cardiac fibers at higher end-diastolic (ED) volumes increases myofilament Ca²⁺ sensitivity over the normal fiber operating range of 1.6–2.1 μm (5). In studies with skinned and intact cardiac fibers the maximal force that can be developed increases with sarcomere length up until 2.1–2.3 μm. However, the cellular mechanism of increased myofilament Ca²⁺ sensitivity during stretch remains unresolved. Increases in force development might be facilitated by an increase in cross-bridge kinetics and or an increase in the force developed per cross-bridge formed.

One frequently reported consequence of stretch is that the probability of cross-bridge binding and their transition to strong attachments (force-producing state) increases as the distance between myosin and neighboring actin filaments decreases (3,5–11), as sarcomere length increases within the normal operating range. There is no doubt that an increase in the affinity of troponin-I for Ca²⁺ promotes more rapid cross-bridge cycling (thin-filament activation). However, it is unclear whether cross-bridge binding to actin results in an increase in the affinity of troponin for Ca²⁺or increased binding of Ca²⁺ to troponin recruits more strong cross-bridges to actin (12). Many research groups have suggested that myofilament Ca²⁺ sensitivity is increased during stretch as a direct result of reduced interfilament spacing (7,12,13). Here, the assumption has been that intact cardiomyocytes maintain constant cell volume behavior, and therefore interfilament spacing is inversely related to sarcomere length.

Much of the evidence for a role of interfilament spacing in determining Ca²⁺ sensitivity stems from observations that Ca²⁺ sensitivity can be increased by controlled osmotic compression of the myofilament lattice (11,13,14). Others have suggested that interfilament spacing is poorly correlated with Ca²⁺ sensitivity (8,15). More recently, another study has shown that interfilament spacing alone cannot explain changes in Ca²⁺ sensitivity (16). It now seems more likely that Ca²⁺ sensitivity is determined by changes in the structure of myosin filaments (12,16).

One recent study of the length-tension relation in isolated cardiac muscle demonstrated with synchrotron x-ray diffraction that at longer sarcomere lengths there is proportional increase in the number of cross-bridge attachments, rather than a change in the average force produced by each myosin head (10). Nevertheless, it still remains to be investigated if there is an increase in myosin heads close to actin and presumably cross-bridges formed in association with an increase in cardiac force when cardiac muscle is stretched in the intact heart.

The aim of this study was to determine if sustained increase in venous return to the heart significantly decreases myosin interfilament spacing and increases cross-bridge formation within a localized region in the epicardium of anterior LV of rat hearts. We found that the relative mass of myosin heads in proximity to actin in systole, as estimated by the change in intensity ratio of the 1,0 and 1,1 equatorial x-ray reflection intensities (I_1,0/I_1,1), increased with global measures of contractile function. Since ED intensity ratio was unchanged by stretch, the proportion of myosin heads close to actin before activation was similar. Systolic intensity ratio was inversely correlated with the maximum and minimum of the first derivative of LV pressure (dP/dt_max) before and during volume loading. End-systolic (ES) LV pressure (LVP) was not significantly elevated by volume loading, but was correlated with the minimum intensity ratio. Therefore, the reduction in interfilament spacing caused by stretch initiated a greater activation of force-producing cross-bridges in early contraction. Volume loading did not result in increased interfilament spacing change during the cardiac cycle in direct proportion to stroke volume (SV) or cardiac output. This study demonstrates that acute volume increase in the intact heart evokes a proportional increase in the number of cross-bridges and rate of force generation that is the result of greater proximity of myosin filaments to actin during contraction.

METHODS

Animals and surgical preparation

Anesthetized (sodium pentobarbital 50 mg · kg⁻¹, intraperitoneal) male Sprague-Dawley rats aged 9–10 weeks (350–400 g, obtained from SLC, Kyoto, Japan) were artificially ventilated (O₂ enrichment 1l · min⁻¹, tidal volume 0.4 ml, ventilation rate 50 min⁻¹). In preliminary experiments we established that adequate pentobarbital anesthesia could be maintained if rats were given supplemental doses (30–40 mg · kg⁻¹ · h), as confirmed by the lack of withdrawal reflexes and the absence of rapid blood pressure fluctuations associated with pain (constant monitoring). However, pancuronium bromide was used in final experiments in addition to anesthesia to be certain that large fluctuations in venous return due to spontaneous ventilatory movements of the rat during diffraction recordings were prevented when the ventilator was briefly switched off during measurements. Rats were then thoractomized before muscular blockade with pancuronium bromide (Mioblock, Sankyo, Tokyo, Japan). The heart and lungs were continuously irrigated with a drip to prevent drying. A catheter in the right jugular vein was used for fluid replacement (lactate Ringers solution, Otsuka Pharmaceuticals, Osaka, Japan after initial 50 units of heparin), maintenance of pH balance (8.4% sodium bicarbonate, Meylon, Otsuka Pharmaceuticals), and drug delivery.

The apex was then raised and partly restrained by two superficial sutures in the LV to eliminate vertical movements during recordings and thus limit changes in myocardial depth. P-V loops were recorded from an apically inserted 1.4 F micromanometer (SPR-671, Millar Instruments, Houston, TX) and a 1.5 F conductance catheter (S-I Medico-tech, Osaka, Japan) with distal placement near the aortic valve (17). Body temperature was 36.5°C–37.5°C. Conductance volume (μl) recordings were calculated from LV blood volume as described elsewhere (17) and calibrated against a cuvette of known volumes filled with blood at 37°C–38°C to obtain an absolute LV volume (LVV, μl). At the synchrotron a parallel conductance correction for absolute LVV was not performed to determine the conductance due to LV mass (by subtraction of the conductance attributable to cardiac muscle). Heart rate (beats per minute (bpm)) was determined from the interval between ED events in the P-V loops. The investigations conformed with the Guide for the Care and Use of Laboratory Animals published by the U.S. National Institutes of Health (NIH Publication No. 85-23, revised 1996) and the guidelines of SPring-8 for the care and welfare of experimental animals.

X-ray source, camera, x-ray diffraction, and analyses

The third generation synchrotron radiation source SPring-8 in Harima, Japan (Japan Synchrotron Radiation Research Institute) produces highly collimated (high degree of parallelism) x-ray beams with sufficient photon flux to record diffraction patterns from muscle fibers within a much shorter exposure time than in the past (5–15 ms). All measurements in this study were conducted at the 40XU beamline (18) in SPring-8 (Hyogo Prefecture, Japan), available for public research use. A collimated quasimonochromatic beam (wavelength 0.08 nm) of dimensions 0.2 mm (horizontal) × 0.1 mm (vertical) was focused on the surface myocardium at an oblique angle to the LV long axis from the left thorax (rat ∼3 m from the detector) as described subsequently. Beam flux was reduced to ∼10¹² photons · s⁻¹ (15 keV and ring current 60–100 mA) by the front slits and a 3-mm aluminum attenuator during measurements, each lasting <2.1 s. Pentobarbital anesthesia was continued during experiments at supplemental rates of 40 mg · kg⁻¹ · h.

The ventilator was briefly stopped at end-expiration to reduce heart movements and large changes in venous return during recording. Image sequences (12 bit, 144 × 150 pixels) were collected at a sampling interval of 15 ms with the aid of an image intensifier (V5445P, Hamamatsu Photonics, Hamamatsu, Japan) (19) and a fast charge-coupled device camera (C4880-80-24A, Hamamatsu Photonics) and then digitally recorded using HiPic32 software (version 5.1.0 Hamamatsu Photonics). Simultaneously the P-V analog signals and the frame timing signal were recorded with an independent data acquisition system (1000 Hz sampling frequency). LV was positioned so the beam passed through the anterior myocardium midway between the apex and the leading edge of the left atrium (free wall between the distal ends of the descending branch of the left coronary artery and the posterior interventricular vein). Beam projection was perpendicular to the spiral fiber direction in the epicardium, as described by Streeter (20).

Diffraction patterns for all time sequences were analyzed using customized software (HDA version 3.0) designed by one of us (N.Y.). This program calculated the radial average line profile about the center of the spectrum, and the integrated intensity of 1,0 and 1,1 reflection intensities (defined as I_1,0 and I_1,1) (21) were determined from the areas under the reflections peaks. Background subtraction was made using a cubic spline function fitted between user-defined criteria for inner and outer limits of the background radiation distribution on either side of the 1,0 and 1,1 reflections. Averaging the integrated reflection intensities rather than summating them along the arcs underestimated the 1,1 intensity by √3 relative to the 1,0 reflection (22). Thus, the 1,1 intensity was corrected by multiplication by √3. During cardiac contractions the LV wall thickness and therefore the number of fibers that the x-ray beam passes through changes with muscle contraction. Since the absolute equatorial reflection intensities are dependent on the number of fibers in the beam path, we used the intensity ratio (I_1,0/I_1,1) for each data series as an index of the equatorial intensity change. Myosin mass transfer index was defined as the difference in intensity ratio between ED and the minimum ratio during systole. The 1,0 reflection lattice spacing (d_1,0) was automatically obtained from the center of gravity of the integrated 1,0 reflection. The lattice spacing of all patterns was calibrated using the 63.5-nm equatorial reflection of collagen present in a chicken tendon.

Heart orientation and fiber direction during recordings

Vertical alignment was made with the aid of a calibrated laser guide, and the first brief diffraction pattern was recorded. The patterns were then immediately inspected to verify if the beam passed through the uppermost surface fibers throughout the whole cardiac cycle. Subsequently, recordings were made deeper within the LV free wall at increments of 0.3 mm moving in a direction toward the LV chamber. In this study, analyses were limited to epicardial recordings obtained within 0.8 mm of the LV surface (epicardium and upper intermediate layers) with essentially uniform fiber orientations (20,22,23). Lactate ringers was administered (intravenous infusion at 2.0 ml · h⁻¹) and Meylon solutions given intermittently during baseline recordings to maintain blood volume and a stable LVV.

Sustained volume-loading protocol and statistical analyses

The intravenous infusion of lactate Ringer's solution was increased to 60 ml · h⁻¹ and the diffraction recordings commenced immediately. All recordings were complete within 3–4 min of infusion. During the first minute of loading the LVV of each rat was shifted rightward and SV increased by 50% or more. With further infusion SV and LVP increased more slowly with time. After cessation of the loading, LVP and LVV returned to baseline values within 5 min in all hearts. Data are expressed as mean ± SD, where appropriate. Responses to volume loading were compared between hearts with a repeated measures analysis of variance. Linear regressions were used to test for significant correlations. A value of P < 0.05 was considered significant.

RESULTS

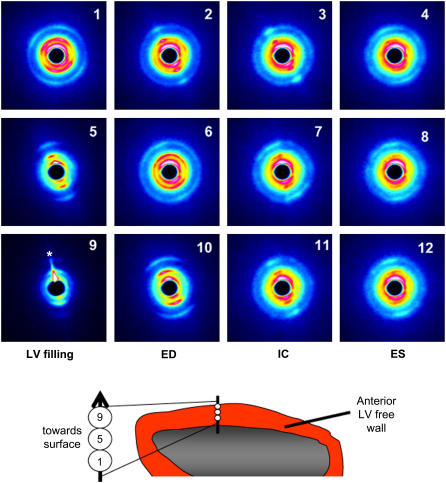
Fig. 1 shows the equatorial diffraction patterns recorded in vivo from the same heart under baseline steady-state conditions for a single cardiac cycle from each of three consecutively recorded sequences in the subendocardial layer (panels 1–4), upper intermediate layer (panels 5–8), and epicardial layer (panels 9–12), respectively. As illustrated in the schema of the same figure, with the vertical step-changes in x-ray beam penetration of the LV wall, the diffraction patterns obtained changed from broad reflection arcs to reflection bands or spots. In the last series of baseline recordings presented (Fig. 1), it can be seen that sagging of the heart during ventricular filling resulted in flaring of the diffraction pattern (indicated by the asterisk in panel 9). In the intervening 15-ms pattern (not shown) recorded between panels 9 and 10, the x-ray did not penetrate any muscle fibers; hence no diffraction pattern was obtained for one of the 11 recorded patterns in that cardiac cycle. Conversely, during systole, fiber-shortening caused the heart to lift particularly at the apex, and the x-ray beam penetrated deeper muscle layers than during diastole of each cycle. Nevertheless, despite this regular shift in the vertical position within the LV wall, the diffraction patterns presented in Fig. 1 demonstrate that this movement (<0.6 mm) was not large enough to cause a shift from one muscle layer to the next during the cardiac cycle. Thus, our diffraction patterns were obtained from the same layer during each recording.

FIGURE 1.

Sequences of pseudocolor diffraction patterns obtained from the same beating rat heart in situ. Each row of patterns illustrates the cyclic changes in reflections obtained from a single muscle layer when the horizontal x-ray beam penetrated the anterior LV wall perpendicular to the long axis of the heart. Diffraction patterns presented were recorded at a sampling rate of 15 ms for a 2-s period but presented here at 30-ms intervals from early diastole (LV filling phase, leftmost column), through to ED, isovolumetric contraction phase (IC) and ES (rightmost column). Every other pattern between the patterns presented here are omitted for clarity. Illustrated are panels 1–4 from the mid-wall (subendocardial layer), 5–8 from the upper-intermediate and epicardial layers, and 9–12 from the surface epicardial layer. Asterisk in panel 9 indicates a flare due to an edge effect. Although the spread of the reflections changes with depth in the LV wall, it is clear from these patterns that vertical restraint limited muscle movements to enable continuous records from the same muscle layer on each occasion.

In all heart experiments the diffraction patterns were recorded at multiple depths within the wall as the x-ray path was shifted from the surface to the center of the chamber or vice versa. The distribution of the equatorial reflections in the superficial myocardium to a depth of ∼0.9 mm consistently changed from a single arc or band about a single equatorial axis to two distinct reflection axes or a split band (an “X” pattern as seen in Fig. 1, panel 1). In beating ex vivo hearts a similar complex pattern was confirmed to originate due to differences in fiber inclination of the spiral epicardial fibers when the beam path passes through both anterior and posterior walls of the LV (22). In this study, however, two distinct spiral fiber inclinations most likely contributed to the X-patterns when the beam passed through both the epicardial and intermediate layers, based on the fiber architecture reported by Streeter (20,24); the axial fiber direction appears inverted at the beam path exit due to the curvature of the LV (22). At depths beneath 1 mm from the surface, the diffraction patterns changed to concentric circles as described for the endocardium (22). Therefore for the purpose of statistical comparisons, hereafter we limited our analyses to include only recordings from x-ray beam alignments that produced patterns confirmed to be derived from the epicardial and upper intermediate layers. Comparison of the diffraction patterns derived only from the epicardial layer was not possible as the epicardial diffraction patterns were lost for part of the cycle due to the heart dropping below the beam during either baseline or volume-loading treatments in some of the hearts investigated.

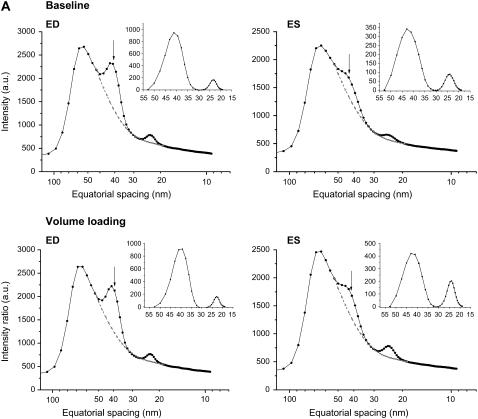
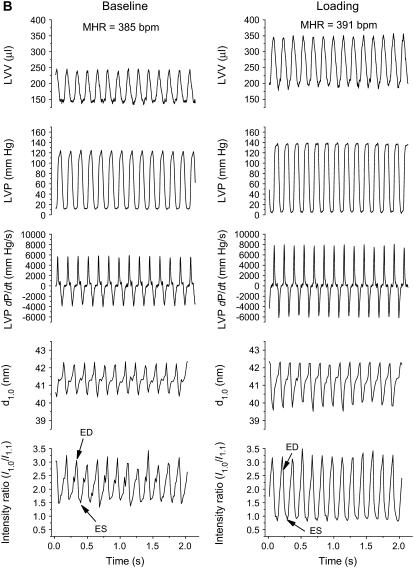
The average reflection intensity profiles and the integrated 1,0 and 1,1 reflection intensities obtained from the same representative heart under baseline conditions and volume loading are presented in Fig. 2 A for a single ED pattern and the ES of the next cardiac cycle. Aside from clear changes in reflection intensities during contraction, a shift in the average d_1,0 spacing was observed during the cardiac cycle (Fig. 2 A, inset panels). Data presented for this same heart over the entire diffraction recording periods demonstrate the beat-to-beat changes in diffraction intensity ratio and myosin interfilament spacing (d_1,0) simultaneous with LVV, LVP, and its derivative (dP/dt) (Fig. 2 B). During the acute volume-loading diastolic peak, LVV was increased by ∼100 μl and SV nearly doubled whereas LVP increased by <10 mm Hg in this heart. Mean LVP dP/dt maximum increased from 5963 mm Hg/s to 7810 mm Hg/s, and the minimum decreased from −4091 mm Hg/s to −5984 mm Hg/s. Taken together these indices suggest that global LV contractile and relaxation abilities were increased significantly by volume loading in this example, whereas ES pressure was unaffected.

FIGURE 2.

(A and B). Examples of changes in equatorial reflection intensities recorded during 15-ms diffraction patterns in a single cardiac cycle and the calculated beat-to-beat changes in intensity ratio (I_1,0/I_1,1), d_1,0, and hemodynamic variables over a series of heartbeats in the same heart. (A) Intensity profiles derived from cardiac diffraction patterns recorded in vivo during baseline and volume-loading conditions illustrate 1,0 (indicated by arrows) and 1,1 intensity peaks at ED and ES. Dashed lines indicate fitted background relations. Inset panels of A indicate integrated reflection intensities. Arrows show the center of the 1,0 peak (d_1,0). (B) Volume loading by intravenous infusion resulted in a significant increase in LVV and SV (maximum LVV − minimum LVV), but a minor change in LVP developed and there was no change in MHR. These global LV functional changes correlated with increased systolic change in intensity ratio and a slightly greater cyclic change in d_1,0.

The regional changes in equatorial intensity ratio and myosin spacing during the cardiac cycle were both amplified by volume loading. The diastolic maximum intensity ratio did not always correlate with ED in all hearts; however, in the example presented in Fig. 2 B the maximum intensity ratio coincided with ED during baseline conditions and oscillated over time between 2.5 and 3.3 (mean 3.05 ± 0.19 SD). Likewise, the baseline minimum intensity ratio occurred generally before ES in each cycle (isovolumetric contraction phase), varying between 1.4 and 1.75 (mean 1.57 ± 0.13 SD). Minimum intensity ratio more or less oscillated in synchrony with the fluctuations in ED intensity ratio on a beat-to-beat basis. Average mass transfer index was 1.54 ± 0.18 (n = 13 beats) under baseline steady-state contractions in this heart. The beat-to-beat changes for the same heart under volume loading showed significant reductions in variability of the intensity ratio at ED and ES between heartbeats (3.24 ± 0.11 and 0.86 ± 0.04, respectively) and to a lesser extent in mass transfer (2.39 ± 0.13).

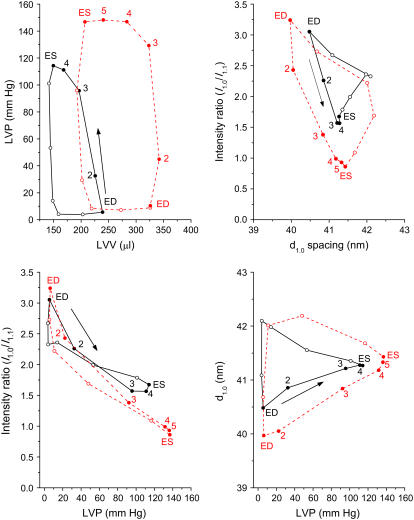
From the LVP, LVV, and x-ray diffraction recordings, such as that presented in Fig. 2, the mean values were determined in relation to the average cardiac cycle for each heart. One such example is presented in Fig. 3. Consistent loops were obtained for the intensity ratio d_1,0 spacing relation, just as LVP and volume always form stable loops, with three or four distinct phases, when ventilatory arrhythmias are eliminated. In some hearts, the distinction between isovolumetric relaxation and filling phases was not obvious (not shown). In all hearts, the systolic intensity ratio decrease after ED (point 0) was mostly completed within the isovolumetric contraction phase. The data presented show that cross-bridges were being formed as LVP and d_1,0 spacing increased with initiation of contraction (Fig. 3). Only a minor secondary increase in intensity ratio during the ejection phase is evident in the example presented in Fig. 3 (0.10 change between points 4 and 5, including ES). Hence, these data suggest that in contrast to skeletal muscle, myosin heads remain in the vicinity of actin filaments during fiber shortening of cardiac muscle.

FIGURE 3.

Mean cyclic changes in LV pressure, volume-intensity ratio (I_1,0/I_1,1) and myosin interfilament spacing (d_1,0) in the same heart during baseline (black solid lines) and volume-loading (red dashed lines) conditions. Data presented are the average loops derived from the time series of Fig. 2. Direction of the cardiac loops is indicated by an arrow in each panel for baseline loops (not different from volume loading). In each cardiac cycle, filled symbols indicate the systolic phase of contraction (ED to ES) and numerals the sequence of data points recorded from ED (point 1) to ES.

In all cases, d_1,0 spacing continued to increase after ES as LVP decreased and intensity ratio increased. A further ∼1 nm myosin spacing increase occurred with little or no LVV change between ES and the start of the diastolic filling phase (point 7 of the cycle from ED in Fig. 3). During volume loading the same interrelationships between d_1,0 spacing, intensity ratio, and LVP were observed during systole and diastole (red lines in Fig. 3). However, ED d_1,0 was 0.5 nm smaller and the systolic intensity ratio change increased by 0.9 (minimum intensity ratio shifted from 1.57 to 0.86) with a mean 22 mm Hg increase in ES LVP relative to the baseline treatment in this heart.

Effect of volume loading on cross-bridge dynamics

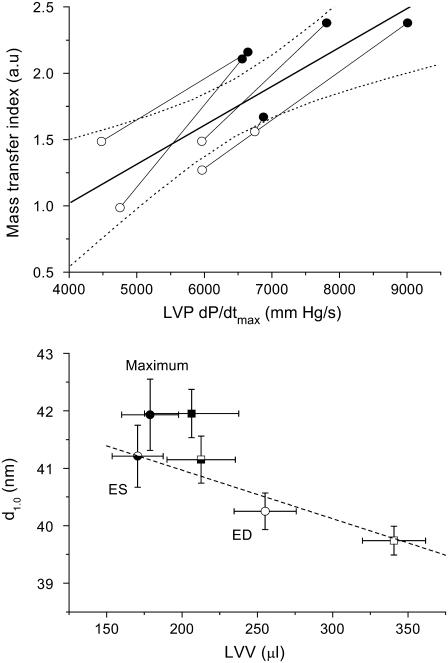
In considering the responses of all hearts in this study, mean heart rate (MHR) and LVP at ED and ES were not significantly changed by the volume expansion (Table 1). Nevertheless, the rates of LVP change during isovolumetric contraction and relaxation periods were increased by 27% and 36%, respectively (dP/dt maximum and minimum, P < 0.05). Consequently, both SV and ejection fraction (EF) were increased in all rat hearts. These changes during volume expansion were paralleled by an increased myosin mass transfer index (Table 1, P < 0.026), as a result of a larger reduction in the minimum systolic intensity ratio (P < 0.048). Although there was a trend for maximum systolic d_1,0 change to increase during volume expansion, this was not significant, as one heart showed a decrease in d_1,0 during systole. When the between heart variability in response to volume loading was examined, we found that the rate of LVP increase during contraction was significantly correlated with myosin mass transfer index (Fig. 4, top panel). An ∼50% increase in the rate of pressure development correlated with a doubling of myosin heads in proximity to actin and presumably the number of strong cross-bridges formed.

TABLE 1.

Summary of mean hemodynamic variables, intensity ratio (I_1,0/I_1,1), and d_1,0 during steady-state contractions before and during volume loading

	Baseline	Volume loading
MHR (bpm)	353.5 ± 34.5	359.5 ± 30.1
EDLVP (mm Hg)	9.2 ± 2.7	10.4 ± 2.4
ESLVP (mm Hg)	113.5 ± 20	132.5 ± 14.1
LV dP/dt maximum (mm Hg/s)	5582 ± 943	7380 ± 1036	P < 0.019
LV dP/dt minimum (mm Hg/s)	−3521 ± −865	−5073 ± −954	P < 0.007
Peak LV pressure/volume ratio (mm Hg/ml)	615.3 ± 164.3	629.9 ± 85.4
SV (μl)	88.7 ± 7.1	139.2 ± 4.3	P < 0.001
EF (%)	34.9 ± 3.5	41.0 ± 2.4	P < 0.014
CO (ml/min)	31.4 ± 4.9	50.0 ± 3.3	P < 0.001
ED intensity ratio	2.64 ± 0.38	3.06 ± 0.40
Minimum intensity ratio	1.29 ± 0.35	0.96 ± 0.28	P < 0.044
Mass transfer index (a.u.)	1.36 ± 0.23	2.14 ± 0.29	P < 0.013
Maximum d1,0 change (nm)	1.65 ± 0.38	2.19 ± 0.50

FIGURE 4.

Relation between the number of cross-bridges (mass transfer) developed locally in the anterior wall and the rate of pressure development during contractions of the beating rat hearts (upper panel) and myosin spacing (d_1,0) changes in relation to LVV of the hearts (lower panel). In the upper panel, baseline means (open circles) are connected with volume-loading means (solid circles) for individual rat hearts (n = 5). A significant direct relation between mass transfer index and LVP dP/dt_max is presented for the group (thick line y = 0.00029x − 0.153, P < 0.004; dashed lines indicate 95% CI of mean). In the lower panel, the relation between d_1,0 spacing during systole (interval between ED and ES) for baseline (circles) and volume-loading (squares) treatments and LVV is significant (dashed line y = 42.65 − 0.0084x, P < 0.0001), but on average 1 nm less than the maximum d_1,0 recorded shortly after ES in each cycle. Open symbols indicate ED, half-closed ES and closed symbols the average recorded maximum d_1,0 ± SD in all hearts (typically mean of 8–12 consecutive cardiac cycles).

Interestingly, we found that there was an inverse linear relation (P < 0.019) between d_1,0 and LVV over the systolic phase of the cardiac cycle under baseline and volume-loading conditions between ED and ES (Fig. 4, lower panel). Diastolic relaxation caused an increase in intensity ratio (shown in Fig. 3, top right panel) with little change in LVV, but a further ∼1 nm increase in d_1,0 (Fig. 4). Despite the significant increase in LVV at ED (mean 26%, t-test P < 0.0001) during volume loading there was no significant change in ED intensity ratio (mean 2.64 ± 0.38 vs. 3.06 ± 0.40). In this study, intensity ratio was independent of d_1,0 at ED (P < 0.626 NS). Hence, our results suggest that a similar proportion of myosin heads were positioned close to actin filaments before contraction, but a greater proportion of cross-bridges were activated when the interfilament spacing was reduced during stretch in the dynamically beating heart.

In earlier studies the range of recorded d_1,0 in intact isolated cardiac fibers was 3–4 nm over a sarcomere length of 1.8–2.3 μm (9,10). In this study sarcomere length was not measured in vivo, but our data clearly show that myosin interfilament spacing in the anterior wall of the beating heart is constrained during systole and the filling portion of diastole to a range of <2 nm, under a wide range of filling conditions. Nevertheless, constant lattice volume behavior was observed during fiber shortening and in the resting state.

DISCUSSION

This study is the first to show that regional cross-bridge formation increases in direct proportion with global ventricular pressure development in the intact heart. Therefore in normal myocardium, regional and global mechanisms regulating cardiac contractions are tightly correlated. More importantly, we show that throughout most of the cardiac cycle in vivo interfilament spacing maintains a direct inverse relation to LVV during volume loading. Stretch of the LV wall fibers reduced interfilament spacing as predicted. However, ED intensity ratio was unchanged by fiber stretch, which implies that a similar proportion of myosin heads must have been in proximity to actin filaments at ED. Since stretching the muscle fibers increased systolic intensity ratio (I_1,0/I_1,1) change in proportion to the rate of LVP change (dP/dt_max), we suggest that the rate of local force development was enhanced by increased strong cross-bridge formation in the isovolumetric contraction phase. Taken together our findings suggest that LDA is determined by the number of cross-bridges formed early during contraction and that myosin interfilament spacing plays a direct role in determining the number of cross-bridges that can form attachments at the beginning of a contraction.

Experimental considerations

In all the diffraction patterns analyzed, the scattered reflections consisted of two bands that we attribute to the uniform myofiber orientation of the epicardial layer (20,24). Recently, the change in distribution of reflections in diffraction patterns was described in detail in relation to muscle layers of the LV free wall and confirmed by a model based on reported muscle fiber orientations (22). Since the diffraction patterns are unique to each layer, we used only the recorded patterns that were the same during baseline and loading conditions to ensure that the same muscle layer was used for comparisons. The number of fibers exposed to the x-ray beam during contractions is not constant between cardiac phases, and so statistical comparisons were limited to the intensity ratio of the two equatorial reflections (I_1,0/I_1,1). Nevertheless, as shown in Fig. 2 there was no obvious qualitative difference in reflection intensity profiles between treatments. Finally, the heart rate of the spontaneously beating rat hearts was not changed by the volume-loading protocol. Thus, we are confident that the observed changes in cross-bridge formation are not confounded by changes in the cardiac force-frequency relation.

Cross-bridge formation is directly related to LDA

ED intensity ratio did not show any consistent trend for change with the rightward shift in LVV (40% increase), but on average it was higher during volume loading (3.06 ± 0.40), achieving a value similar to that reported for cardiac muscle under relaxing conditions (3.07 in Matsubara et al. (25)). In an early study of papillary muscle it was shown that myosin heads do not return completely to the resting state close to the myosin backbone when cyclically contracting at a fixed sarcomere length (25–28). However, when papillary muscle is stretched intensity ratio increased under dynamic conditions (29). The minor elevation of ED intensity ratio during volume expansion was not significant (P < 0.057) in this limited study, but would be consistent with changing sarcomere length and improved fiber relaxation. During in vivo contraction, myosin head proximity to actin increased during volume loading, as the minimum intensity ratio was significantly decreased and hence, mass transfer index significantly increased in the same hearts.

Using an alternative approach of recording myocyte enthalpy during contraction, Widén and Barclay showed that under basal steady-state conditions cardiac muscle uses as few as half of the available cross-bridges during a single submaximal contraction (30). More importantly, these authors also demonstrated that the number of cross-bridge attachments is determined early in contraction and is independent of shortening velocity and dependent on calcium release and preload conditions. The lack of change in the intensity ratio during the ejection phase of beating hearts is consistent with the conclusions of Widén and Barclay. Furthermore, our results also support their conclusion that during the sliding of myosin filaments in cardiac muscle, under basal or volume-loading conditions, there is no promotion of further cross-bridge cycling as seen in skeletal muscle.

In contrast to this study of LDA, one study of working papillary muscle at least, has shown that positive inotropy mediated by β-adrenergic stimulation involved increases in the force generated per cross-bridge as a result of calcium-calmodulin kinase-II activation (31). This finding, however, does not preclude cross-bridge number as the principal determinant of cardiac force development in LDA, since LDA is independent of the β-adrenergic pathway (4). We therefore conclude that in the beating heart, LDA-mediated increases in contractile force development are the result of increased cross-bridge recruitment rather than force developed per cross-bridge. This is consistent with an earlier study of intact cardiac fibers (10).

Relations between d_1,0 spacing and sarcomere length

Rodriguez and colleagues (32) provided the first evidence of the normal sarcomere operating range in beating canine hearts using a cineradiography approach. Transmural gradients in sarcomere length were reported in the same study. However, it is less clear if significant gradients exist in the LV free wall of rodent hearts. Grimm et al. (33) found no gradient in arrested rat heart sarcomeres (mean 2.04–2.08 μm at normal EDLVP). On the other hand, fiber shortening was reported to be ∼0.3 μm during systole in the anterior wall, irrespective of muscle layer in the canine heart (32). More recently, the sarcomere length operating range of the endocardial muscle layer in the closed chest mouse was estimated to be 1.9–2.1 μm (34), based on assumptions of constant myosin lattice volume behavior and similar inverse relations between d_1,0 spacing and sarcomere length in both intact isolated cardiac muscle (10) and the in situ beating heart.

In our study, myosin spacing cycled between 39.5 nm and 42.5 nm under steady-state contractions (Fig. 4). Using the same approach of Toh et al. (34) we estimate the ED sarcomere operating range as 1.75–1.90 μm in the epicardial layer over the range of LVV examined. This ED value agrees well with previous reports based on histological inspection of perfusion-fixed myocardial samples (1.96 μm (33) and 1.83 μm (35) in the rat and between 1.82–1.95 μm in the rabbit (36)) but is shorter than the closed chest murine heart (endocardium ∼2.1 μm (34)) and the canine heart (2.13 μm (37)). Direct measurement of sarcomere length in the beating heart is required to determine if real differences exist between species and if in vivo sarcomere length is affected by open-chest conditions.

Interfilament spacing change during the cardiac cycle

Farman and colleagues (38) have now demonstrated that during isometric contractions myosin interfilament spacing is the same during diastole and systole after taking into account sarcomere length. A carefully planned protocol employed gated x-ray diffraction recording during sarcomere length clamping at rest (ED) and peak force (isovolumetric contraction). However, interfilament spacing during the relaxation phase was not explored. In support of that study, we show here for the first time to our knowledge that force generation in the LV free wall results in a linear increase in myosin interfilament spacing during systole (Fig. 4). This relation appears to be dependent solely on sarcomere length, since the same relation held during LDA.

An important question arises from this study as to whether in vivo interfilament spacing increases at a lower than expected rate during sarcomere shortening on the basis of sarcomere length, when compared to the sarcomere length-d_1,0 relation of relaxed muscle. We cannot directly answer this question without first measuring in vivo sarcomere length. Nevertheless, the findings of our study suggest that myosin interfilament spacing is constrained by strong cross-bridge attachments during sarcomere shortening. First, the cyclic changes in myosin interfilament spacing we recorded suggest that peak myosin lattice spacing, and presumably the shortest sarcomere length, occurred after ES when LVP was on the decline (Figs. 3 and 4). Although we found that myosin spacing was inversely related to ventricular volume throughout systole, a further 1-nm expansion occurred during the isovolumetric relaxation phase of the PV cycle. It is unlikely that the timing of the d_1,0 peak recorded in the anterior wall is attributable to a regional difference in the velocity or extent of fiber shortening relative to global LVV change in the normal heart (32).

Lew and Le Winter have shown that longitudinal subepicardial fibers do not shorten more in anterior wall than elsewhere (39). Rather, the same diffraction patterns we used to derive myosin spacing changes over the cardiac cycle show us that myosin interfilament spacing was continuing to increase whereas intensity ratio rapidly increased after ES. This can only be interpreted to mean that myosin spacing increased as a consequence of detachment of the cross-bridges after blood ejection is completed. Elastic recoil of fibers due to the laminar sheets of extracellular matrix between the fibers would be expected to reduce myosin spacing when cross-bridges detach during the relaxation phase. Thus extracellular elasticity cannot explain the continued lattice expansion beyond ES, but it might contribute to a reduced cyclic change in interfilament spacing during stretch associated with volume loading if the coiled perimysial collagen fibrils in between the myocardial sheets stretch more than the myocytes (40). On the other hand, many research groups have demonstrated that radial cross-bridge forces compress lattice spacing during contraction (41–44).

Based on data presented by Toh and colleagues (34) the same spacing increase seen in this study of rat hearts appears to be true of murine hearts as well, since the maximum d_1,0 spacing was generally recorded ∼90 ms after ED, subsequent to the minimum systolic intensity ratio (presumed to be ES) that was reached at 50 ms. We therefore suggest that in rodent hearts at least, myosin spacing is constrained by the attached cross-bridges during steady-state contractions. Thus, although an inverse linear relation between myosin interfilament spacing and LVV (and possibly sarcomere length) exists, we suggest that constant lattice volume in the intact heart is only restored after systole by the yet unexplained increase in spacing. The large radial stiffness of the myosin heads at large d_1,0 is predicted to cause lattice expansion upon deactivation (41,42). Spring-like release of the cross-bridges might therefore explain the post-ES interfilament spacing increase of ∼1 nm. Having shown that cross-bridge formation is essentially determined by the preload conditions and therefore independent of shortening velocity, it will be possible to evaluate how genetic manipulations of contractile proteins or disease states influence local muscle contractility during LDA. Further work is required to establish how myosin interfilament spacing relates to sarcomere length over the entire cardiac cycle in the intact heart.