Phenotypic variability of growing cellular populations

Abstract

The dynamics and diversity of proliferating cellular populations are governed by the interplay between the growth and death rates among the various phenotypes within a colony. In addition, epigenetic multistability can cause cells to spontaneously switch from one phenotype to another. By examining a generalized form of the relative variance of populations and classifying it into intracolony and cross-colony contributions, we study the origins and consequences of cellular population variability. We find that the variability can depend highly on the initial conditions and the constraints placed on the population by the growth environment. We construct a two-phenotype model system and examine, analytically and numerically, its time-dependent variability in both unbounded and population-limited growth environments. We find that in unbounded growth environments the overall variability is strictly governed by the initial conditions. In contrast, when the overall population is limited by the environment, the system eventually relaxes to a unique fixed point regardless of the initial conditions. However, the transient decay to the fixed point depends highly on initial conditions, and the time scale over which the variability decays can be very long, depending on the intrinsic time scales of the system. These results provide insights into the origins of population variability and suggest mechanisms in which variability can arise in commonly used experimental approaches.

Cellular populations are rarely collections of homogeneous cell types, even when the cells share the same genetic makeup. Differences in cell size, growth rate, and morphology are common and greatly contribute to the overall variability of the population. Often, these variations are due to stochastic fluctuations that can occur at many different scales (1–4). For instance, noise contributes to the traversal of start and progression of yeast cells into the cell cycle (5) and can limit the precision of circadian clocks (6). Furthermore, noise plays an important role in determining the phenotype of cells that exhibit epigenetic multistability. In such cases, the same set of genes can lead to drastically different phenotypic expression depending on the current state of the genes. Epigenetic multistability has been found to play a role in many gene networks including metabolic systems (7–9) and bacterial persistence (10–12). Similarly, noise also appears to underlie the emergence of neural precursor cells from an initially homogeneous population during the development of Drosophila melanogaster (13), and random fluctuations influence the fates of cells infected with HIV (14).

Noise occurring at both the genetic and molecular level has been intensively studied in the past few years (1–3, 15,16–18), and multiple sources can contribute to the observed variability (19). Researchers have classified noise into two general classes: intrinsic noise, which stems from the low numbers of reactants involved in gene expression and regulation, and extrinsic noise, which arises from all other sources such as environmental fluctuations (20, 21). Noise in gene expression can be propagated through network cascades, and the corresponding amplitude of the fluctuation (as measured by a protein concentration, for instance) is affected by the details of the network (22–26). However, variability at the molecular level is often not the sole consequence of stochastic fluctuations. Genetic noise can lead to macroscopic level fluctuations of entire cellular populations because different types of cells usually have distinct responses to various environments and will therefore have different growth rates and survival capabilities (20, 21, 27–29). Additionally, the switching of individual cells from one epigenetic phenotype to another can lead to dramatic changes in the overall variability of an entire population (30). Diversity of cellular populations, as measured by the overall numbers of specific phenotypes (31–33), is therefore expected to be affected by the stochasticity inherent to gene regulation.

In this article, we study the effects of epigenetic multistability on population diversity. We first introduce a generalized form of the relative variance (the square of the coefficient of variation), which is closely related to Simpson's index (34) and takes into account the variability both within a single colony and between multiple, distinct populations. Next, using a two-phenotype community as an example, we analytically and numerically investigate the propagation of the relative variance in different environments. We find that the variation in a population depends highly on its initial state and corresponding environments: Different initial conditions result in permanent differences of variation in unbounded growth environments, whereas variability arising from initial conditions in growth-limited environments (such as logistic growth or microfluidic chemostats) eventually decays away. However, this transient decay of the variability can occur on time scales that are longer than the typical duration of many experimental procedures. Furthermore, the type of growth limitation placed on the population can affect the final steady-state variability. Therefore, our findings suggest that care must be taken when designing experiments to measure the variability of multistable cellular populations. If the transients are not given a sufficient amount of time to decay or the type of growth limitation is not taken into account, then conclusions drawn from such experiments may be faulty.

Results

Generalized Relative Variance.

To illustrate the effects of stochasticity on cellular population variability, we examined the simple two-phenotype community shown in Fig. 1a. Each type of cell can divide, die, and switch to the other type. We assume that the cells grow in an idealized microfluidic chemostat-like environment (35) in which there is a maximum possible number of cells (N_max, say) but that the growth rates of the cells are not limited by the overall population. In such an environment, once the population maximum is reached, subsequent cellular divisions are still possible, but this population growth begins to push cells out of the chemostat. To simulate this, we used a modified version of Gillespie's algorithm (36). Each time the total population reached N_max + 1, one cell (chosen at random) was taken out of the population. The simulations were run for a finite amount of time, representing six doubling times of the fastest growing phenotype, which is typical for experiments performed in microfluidic chemostats. At that time, the numbers of each type were recorded, and the trial was started anew. Fig. 1b shows the coefficient of variation (CV) for the number of each phenotype versus the number of trials averaged for two different initial conditions. When the initial conditions are such that there is only one cell of each type present in the system, the CV for each type is very large when compared with the corresponding CVs for large starting numbers (100 cells of each type). Also note that the number of trials necessary for the CV to converge to its true average is very large. This last point leads us to examine a generalized form of the relative variance, which measures the variability of the overall diversity of population and takes cross-colony variability into account.

Fig. 1.

Variability in bistable cellular populations. (a) A two-phenotype community. Each phenotype (green and red) has its own birth rate (γ₁, γ₂) and death rate (δ₁, δ₂). They are able to switch from one phenotype to the other with the transition rates τ₁₂ and τ₂₁. (b) Coefficient of variation (CV) versus sample number. A two-phenotype community (illustrated by a) grows in a microfluidic chemostat, which can contain a maximum of 200 cells. Green and red curves are the CVs of phenotype 1 and 2 with the initial state 1:1, respectively, whereas blue and magenta curves are for the initial state 100:100. Here, γ₁ = 1.0, γ₂ = 0.5, δ₁ = δ₂ = 0.01, and τ₁₂ = τ₂₁ = 0.01. Time is in units corresponding to the number of deterministic generations of the fastest growing phenotype. Each trial was simulated for six generations of the faster growing phenotype (t ∈ [0,6]).

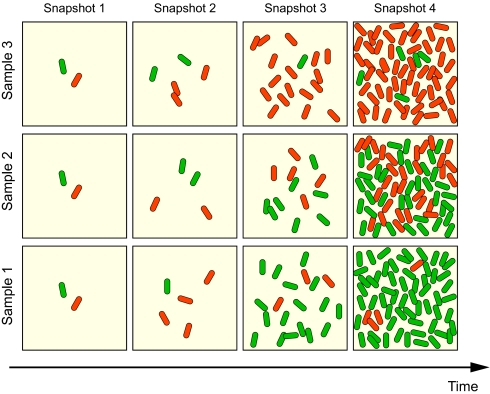
For the simple system depicted in Fig. 1, the overall variability measured arises from the stochastic nature of the growing system. Even with the same initial conditions, different trials may lead to drastically different outcomes. For instance, consider the initial condition in which there is only one cell of each type. Some random trajectories may lead to the dominance of one phenotype or another, or neither may dominate. Snapshots of possible trajectories with the same initial condition are shown in Fig. 2.

Fig. 2.

An illustration of the ensemble population diversity. The initial state 1:1 is the same for each set of snapshots. Here, the colors represent distinct phenotypes. Cells grow, divide, and die according to the dynamics shown in Fig. 1. Four snapshots are taken at specific times for each trial.

One way to measure the diversity of a cellular population was first introduced by Simpson (34). For a community with S cellular types (either genetic or phenotypic) and n_i cells for phenotypes i ∈ {1, 2, …, I}, Simpson proposed a “concentration,” θ, to measure the diversity, where θ = 1/N²Σ_i=1^Sn_i², and N = Σ_i=1^Sn_i is the overall population of the community. Similar quantities have been introduced in the study of spin glass dynamics and in the interpretation of single-molecule dynamics (37, 38). Quantitatively, Simpson's concentration describes the probability that any two randomly chosen individuals from a community are of the same type. Therefore, the complement of the concentration, 1 − θ, termed the Simpson index, describes the probability that two randomly picked individuals are different types of cells. Thus it is a measure of the population diversity of a particular community. However, the population for each phenotype can vary from one trial to the next, and the index proposed by Simpson does not account for this. This cross-colony variability has long been known to exist in genome diversity (39), and the effects it has on various measures of population diversity have been studied (40). Here, we investigate population variability, taking into account variability between colonies by introducing a generalized relative variance [detailed in supporting information (SI) Text]:

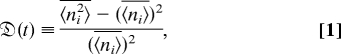where n_i = n_i(t) is an element of the S-dimensional vector n(t) and represents the population of phenotypes i at time t; the bracket operator, 〈(·)〉 ≡ 1/S(Σ_i=1^S)(·), represents averaging over cell type within a given population; and the bar operator, (·) ≡ Σ_nP(n, t|n₀, t₀)(·), is the ensemble average over the population distribution of possible communities. Here, P(n, t|n₀, t₀) is the probability that the colony has a population n at time t, given that it initially started with population n₀ at time t₀ < t. Experimentally, one can estimate P(n, t|n₀, t₀) by performing multiple trials with the same initial condition. Theoretically, however, the moments of P(n, t|n₀, t₀) required to calculate (t) can sometimes be calculated analytically, even if the entire distribution itself cannot.

The relative variance, (t), is in a convenient form, because it can be separated into two terms that measure the variability due to intracolony and cross-colony contributions. In particular, we write

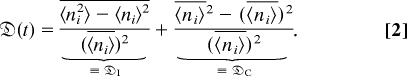The first term, _I, the intracolony variance, measures the mean population variation, averaged over all trials. It is analogous to the ensemble averaged Simpson concentration and plays a similar role: It is 0 when the population is evenly distributed among phenotypes, increases with the unevenness of population distribution, and reaches its maximum when the entire population belongs to a single phenotype [note that this is the opposite of the definition of species diversity (34)]. The second term, _C, termed the cross-colony variance, measures the population variation among colonies. It goes to 0 when the overall population is the same from colony to colony and becomes large when the variation in population size is large among colonies. These two variances have some analogy to the notations of intrinsic and extrinsic contributions to the noise in gene expression (19). Here “intrinsic” refers to the intracolony variance, whereas “extrinsic” refers to cross-colony variance. The generalized relative variance is simply related to Simpson's index when we neglect population dispersion, i.e., when the distribution of population size is a δ-function. In such cases, _C = 0 and _i = (〈n_i²〉 − 〈n_i〉²)/〈n_i〉² = Sθ − 1, where θ is the Simpson concentration (34).

Unbounded Growth Environments.

To examine the dynamics of the generalized relative variance in more detail, we study the variability of our simple model in two different environmental settings. We first investigate the variation of populations growing in an ideal case in which there are no constraints on nutrition or space. We use the two-phenotype community as an example to explore the variation as shown in Fig. 1. The population dynamics can be described by the following master equation:

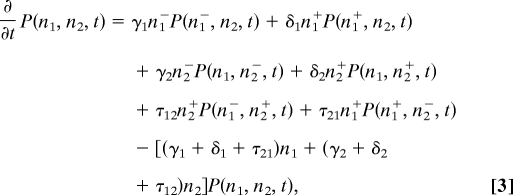where γ_i and δ_i are the rates of birth and death for phenotype i respectively, τ_ij is the transition rate from type j to type i, and n_i^± = n_i ± 1 for i ∈ {1, 2}.

As it turns out, the expression for the relative variance, Eq. 1, can be recast into a function of the first two moments of P(n, t) (see SI Text). Therefore, it is only necessary to calculate these moments, instead of P(n, t) itself. In most cases, exact equations describing the evolution of the first two moments cannot be derived analytically from the master equation. However, for our simple two-phenotype model, they can be derived, and they furthermore decouple from all higher moments. By constructing a vector consisting of the first and second moments as M(t) = (n̄₁(t), n̄₂(t), n₁²(t), n₂²(t), n₁n₂(t))^T, we may write

where the matrix Q is given by

and σ₁ = γ₁ − δ₁ − τ₂₁, σ₂ = γ₂ − δ₂ − τ₁₂, ρ₁ = γ₁ + δ₁ + τ₂₁ and ρ₂ = γ₂ + δ₂ + τ₁₂.

Exact expressions of the first moments, M⁽¹⁾(t) = (n̄₁(t), n̄₂(t))^T, and second moments, M⁽²⁾(t) = (n₁²(t), n₂²(t), n₁n₂(t))^T (detailed in SI Text) allow us to study the temporal behavior of the relative variance, which can be expressed as a function of M(t) as

where M_j⁽ⁱ⁾(t) is the jth element of the ith moment at time t. This variation expression is characterized by five exponents, (θ, ν, θ+ν, 2θ, 2ν), where θ = 1/2(σ₁ + σ₂ + Δ), ν = 1/2(σ₁ + σ₂ − Δ), and $\Delta =\sqrt{{\left({\sigma }_1-{\sigma }_2\right)}^2+4{\tau }_{12}{\tau }_{21}}$. The exponent θ is the largest eigenvalue that asymptotically approaches the Lyapunov exponent for the deterministic exponential growth of the dynamic systems at the long-time limit (21).

We also studied the propagation of the population variation in an unbounded growth environment for different initial states (see SI Text). The result shows that the population variability depends highly on the initial conditions. The total variance approaches an asymptotic value that depends on the initial conditions, even though the rate constants remain the same. The long-time asymptotic behavior of the population is dominated by the largest exponent, 2θ, and the individual contributions in that limit are

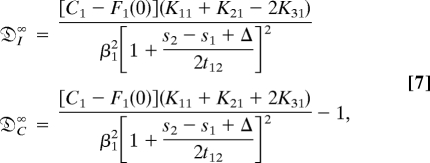where the detailed expressions of C₁, F₁(0), and K_ij are given in the SI Text.

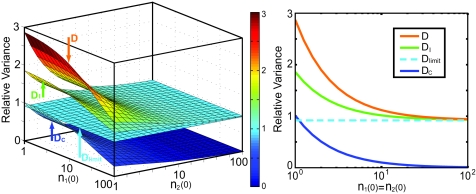
Fig. 3 explicitly shows the effects of the initial states of a cell population on the long-time limit of the relative variance. Fig. 3 Left illustrates the dependence of the variance on its initial population. From bottom to top, the four surfaces correspond to cross-colony (_C), deterministic (_lim), intracolony (_i), and overall population variance (). Here, the variance _lim was calculated from the corresponding mass action (mean-field) dynamics. This relative variance, _lim, is not 0, even though there exists no stochasticity in the equations. The reason is that our definition of the variance requires only that the numbers of each phenotype differ for there to be a nonzero variability. Fig. 3 Right shows a cross-section of the individual contributions to the variability along the diagonal. As shown in both Fig. 3 Left and Fig. 3 Right, smaller initial populations result in larger final population variations. As the size of the initial population increases, the asymptotic value of the overall variance decreases, limiting to the deterministic result, which is independent of the initial conditions. The dependence of the overall variance on the initial population is analogous to the variability seen in gene regulatory networks. In those systems, the small numbers of molecules gives rise to variability in the concentrations of each reactant. The magnitude of this type of variability depends highly on the total number of molecules—small numbers lead to high variability, whereas large numbers lead to low variability (41). Such history-dependent variability has been shown to exist experimentally by Fukami and Morin (42), who studied the diversity of growing aquatic microbial communities with various histories. Fukami (43) later showed that smaller ecosystems resulted in greater diversity, just as our simple model predicts.

Fig. 3.

Asymptotic (t→∞) relative variance with respect to different initial distributions. (Left) The four surfaces correspond to cross-colony, deterministic, intracolony, and total population variance, from bottom to top, respectively. (Right) A cross-section of the variation indices along the line n₁ (0) = n₂ (0). The asymptotic variance differs from the deterministic prediction but approaches it when the initial numbers of cells are large. Initial phenotypes are assumed to be δ-distributed, and parameters are the same as those in Fig. 1b.

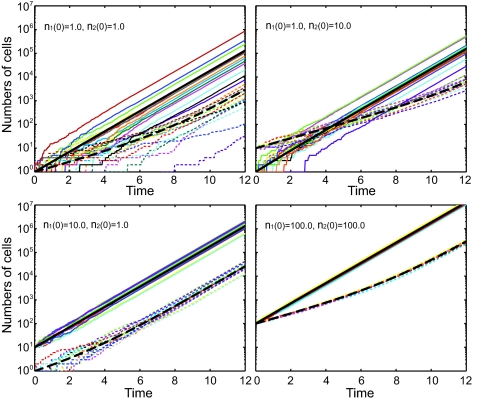
To test our analytical results, we performed numerical simulations (Fig. 1a) using the Gillespie algorithm (36). We averaged 10⁵ trials for each of several different initial conditions. The results show that both the ensemble averaged means and variances of each phenotype agree well with those from analytical solutions. Fig. 4 is a direct illustration of population variability with sample trajectories. It is clearly shown that a community with a small initial population has large variability that persists indefinitely. Communities with larger initial populations have less population variability. To better understand the physical meaning of the variability, we also examined a completely symmetric situation in which the growth, death, and transitions rates were the same between the two phenotypes (see SI Text).

Fig. 4.

Simulation of cellular population dynamics. The upper left, upper right, lower left and lower right images correspond to different initial conditions [(n₁ (0),n₂ (0)) = (1, 1), (1, 10), (10, 1), and (100, 100)]. In each image, the black bold solid and bold broken lines are the mean numbers of phenotypes 1 and 2 from analytical solutions. Each pair of a solid line and a broken line with same color are the two trajectories of phenotypes 1 and 2, respectively, from a single simulation. There are 14 pairs of trajectories shown in each image.

Bounded Growth Environments: Microfluidic Chemostats and Logistic Growth.

Realistic environments in which cellular populations grow generally impose limitations on the cells because of finite nutrients (as in flask cultures or agarose plates) and/or space [as in microenvironments or microfluidic chips (44)]. These limitations can have important consequences on the long-time limit of the population dynamics, and we now examine two specific realizations of bounded growth environments: an idealized microfluidic chemostat model and a logistic growth model.

Ideally, growth in microfluidic chemostats will have an endless supply of nutrients but a capped population. Once the overall population has filled the chemostat, new growth pushes older cells outside the boundaries of the chemostat, where they are flushed away. On average, this means that for every cell grown above the maximum, one cell will be randomly taken out of the population.

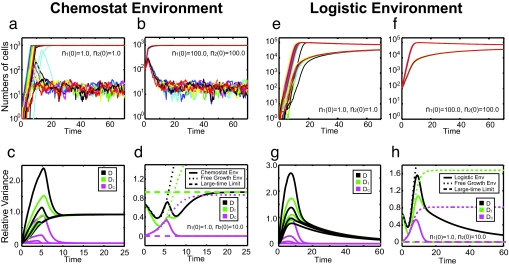
To examine the effects of this type of limited population growth, we performed numerical simulations using the modified version of the Gillespie algorithm. Fig. 5 a and b shows typical trajectories from these simulations for populations with the initial conditions (n₁ (0), n₂ (0)) = (1, 1) and (100, 100), respectively. Trajectories from different runs are represented by different colors. Now, the variance reaches a unique long-time limit, independent of the initial conditions. However, the transient variability still depends highly on the initial conditions and can persist for many generations. Also, depending on the initial population size, the transient variability can become quite large, especially when the initial population is small. When the initial population is near the maximum allowed by the chemostat (N_max = 1,000, here) the transient variability is much smaller.

Fig. 5.

Relative variances in chemostat and logistic environments. (a and b) Typical trajectories of cell populations obtained from Gillespie simulations. In a, the initial state is n₁ (0) = n₂ (0) = 1, and in b, it is n₁ (0) = n₂ (0) = 100. The different colors of the curves represent trajectories from different runs. The maximum population here is 1,000, and other parameters are the same as those in Fig. 1b. (c) The relative variances converge in chemostat environments. Green, magenta, and black sets of curves correspond to intracolony, cross-colony, and overall variances, for different initial conditions [from top to bottom: (n₁ (0),n₂ (0) = (1, 1), (3, 3), (10, 10), and (100, 100)]. After a transients decay, the cross-colony variance goes to 0, whereas the intracolony variance asymptotically approaches a fixed point, regardless of initial condition. (d) Comparison of the relative variances in chemostat environments to those in unbounded growth environments. The solid curves were from direct simulation of the system in Fig. 1b using the modified version of Gillespie's algorithm for chemostat-like environments. The dotted lines are the short time (t 0) limit predicted from the unbounded growth environment, and the dashed lines are the theoretically predicted long-time limits. The corresponding results of the logistic growth are displayed in e–h. The coloring and the symbol scheme of the lines have the exactly same setup as those of the chemostat case. Parameters are chosen: γ₁⁰ = 1.0, γ₂⁰ = 0.5, τ₁₂ = τ₂₁ = 0.01, δ₁⁰ = δ₂ = 0.01, λ₁ = λ₂ = 1.0, and N_equ = 10,000. Again, the dynamics of the cell numbers are shown in e and f, whereas the variances are shown in g and h for initial conditions (1, 1) and (100, 100), respectively.

Fig. 5c shows the dynamics of intracolony, cross-colony, and overall variances in microfluidic chemostat environments. All of the relative variances starting from different initial states converge to the same asymptotic values. Moreover, cross-colony variations go to 0. This is consistent with the previous statement that cross-colony variation goes to 0 when the population is the same from colony to colony because the overall populations here are constrained to be identical in chemostat environments.

For the relative variance of the chemostat environment, asymptotic expressions for both t → 0 and t → ∞ can be calculated, and match well with simulations. For instance, the steady-state (t → ∞) distribution for the number of type 1 can be written as

where P(0) is a constant determined by normalization. From this, and a similar expression for P(n₂), one can then derive a theoretical estimate of the overall relative variance (see SI Text for details).

For short times, and particularly when the overall population is still much smaller than N_max, the population variability is very close to the variability that would occur for the same colony under unbounded growth conditions, as shown in Fig. 5d. Also shown are the long-time limits of the intracolony and cross-colony contributions (Fig. 5d, dashed lines). Initially the variations for the chemostat and the unbounded growth environment are identical, because the initial population in the chemostat is small and the population cap is not a factor. Once the chemostat culture has had time to grow, however, the population maximum begins to affect the dynamics, and the variability diverges from those in the unbounded growth environment. Finally, the variance of the chemostat population converges onto its steady-state value.

For populations of cells that are limited in their overall population maximum (because of either nutrient or spatial limitations), the final variability will eventually converge to a steady-state value. However, the value of the final variability will depend on the type of limitation placed upon the population. To illustrate this point, we examined the same population of cells as above but now in a logistic growth environment (45). In other words, we make the substitution γ_i → γ_i⁰[1 − (n₁ + n₂)/N_equ] for the growth rates, where γ_i⁰ is the maximum growth rate of phenotype i, and N_equ is the overall population maximum. As we show in Fig. 5 e–h, the resulting logistic growth variability is drastically different from that found in microfluidic chemostats. Although the transient variability (i.e., when n₁ + n₂ ≪ N_equ) is still governed by the free growth limit, the asymptotic values of the variability have changed.

This qualitative change in the asymptotic behavior of the variability can be understood by examining the dynamics of the system once the population has reached the maximum. In the chemostat environment, the overall population size ceases to increase, but the cells themselves can still grow and divide (resulting in random cell loss). This means that the final variability will depend on both the growth and transition rates. In contrast, the logistic growth environment essentially stops growth altogether once the population has reached its maximum. There will still be some growth that occurs to replace dying cells, but to first order this can be ignored (see SI Text). Therefore, the asymptotic variability in the logistic case will be determined only by the transition rates. In the case that the transition rates are symmetric (i.e., τ₁₂ = τ₂₁) the population will consist of N_equ/2 cells of each phenotype, meaning that the intracolony variability will go to 0 (as shown in Fig. 5 g and h).

Conclusions and Discussions

Using a two-phenotype community as a generic example, we examined the propagation of population variations in different environments and with different initial conditions. We found that the initial state can greatly affect the overall variability of a population, especially in unbounded growth environments. In general, we found that the dependence of the relative variance on the initial conditions persists indefinitely. When there exists a constraint on the overall number of cells, such as in microfluidic chemostats and logistic growth environments, we found that the overall variance converges to a unique fixed point, regardless of the initial conditions.

Although any conceivable experimental situation must have some limitations on the growth of cells, the transient variability induced by the initial conditions can still play a major role. Depending on the transition rates between phenotypes, the decay time of the transient can be much longer than the rate of population growth. This means that it is possible to have, for instance, a chemostat that has become completely filled with cells yet has not reached equilibrium in terms of its diversity. One may have to wait an extremely long time for the steady state to be reached, and this might not be practical.

These issues are particularly important when dealing with cellular populations in microfluidic devices. Although many of these devices are designed to work as chemostats, clogging and cellular crowding are still common, and it is rare that healthy cellular growth continues once the chamber has been filled. For this reason, it is often preferable for experimenters to begin with just a few cells (even as few as one), to maximize the amount of time available for imaging. Therefore, the transient variability can be quite large in these situations. Furthermore, because most experimental trials using microfluidic devices end once the chamber has been filled, the diversity of the population may never equilibrate. Therefore, care must be taken when designing experiments to measure cellular diversity so that the initial condition dependence of the variability is taken into account.

To further complicate matters, the dynamics of the system at the population maximum can have a large affect on the measured variability. Depending on how much growth occurs at the population maximum (to replace cells that have either died or been washed away), the variability will change. As mentioned above, experiments run in microfluidic devices tend to overgrow the imaging chamber, even when they are designed to expel excess cells. In this situation, the dynamics of the population may be a mixture of our idealized chemostat and logistic growth environments—meaning that the true growth characteristics of the population at its maximum will be very complicated. Therefore, it may be preferable to start experiments from an initial population of one cell, even though such colonies have a large transient variability (see SI Text). If colonies started from single cells can be grown for a sufficient amount of time before the growth limitations begin to take effect, the measured variability will be independent of the type of growth limitation.

Materials and Methods

The stochastic simulations in this study were performed with the Gillespie algorithm (36) and consisted of the six events shown in Eq. 2, where G and R represent the two different phenotypes (green and red in Fig. 1).

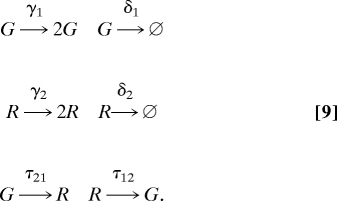For simulations involving unbounded growth environments, the populations were allowed to change freely. Simulations of populations in idealized chemostat environments were subjected to a maximum population constraint, limiting the total number of cells to N_max. These simulations were run in the same manner as the unbounded-growth environment simulations, except that each time the total number of cells reached N_max + 1, a single cell was removed from the population. The type of cell removed was chosen randomly, with the probability of a cell of type i being removed given by n_i/Σ_in_i, where n_i is the number of cells of type i. Simulations of populations in logistic environments were performed in the same manner as the unbounded growth environments except that growth rates depended on present populations, i.e., growth rates can be expressed by γ_i = γ_i⁰ (1 − Σ_iλ_in_i/N_equ), where γ_i⁰ and λ_i are the corresponding rate and relative weight, and N_equ is the overall equilibrium population. Growth rates therefore are updated in the simulation once the populations change. Simulations for each initial condition were performed 10⁵ times, and the populations of each type were recorded after each trial. The various measures of variability (CV and relative variance) were calculated according to their definitions.