Skeletal muscle resists stretch by rapid binding of the second motor domain of myosin to actin

Abstract

A shortening muscle is a machine that converts metabolic energy into mechanical work, but, when a muscle is stretched, it acts as a brake, generating a high resistive force at low metabolic cost. The braking action of muscle can be activated with remarkable speed, as when the leg extensor muscles rapidly decelerate the body at the end of a jump. Here we used time-resolved x-ray and mechanical measurements on isolated muscle cells to elucidate the molecular basis of muscle braking and its rapid control. We show that a stretch of only 5 nm between each overlapping set of myosin and actin filaments in a muscle sarcomere is sufficient to double the number of myosin motors attached to actin within a few milliseconds. Each myosin molecule has two motor domains, only one of which is attached to actin during shortening or activation at constant length. A stretch strains the attached motor domain, and we propose that combined steric and mechanical coupling between the two domains promotes attachment of the second motor domain. This mechanism allows skeletal muscle to resist external stretch without increasing the force per motor and provides an answer to the longstanding question of the functional role of the dimeric structure of muscle myosin.

Skeletal muscle primarily acts as a machine that uses metabolic energy to drive macroscopic movements of the body. When an active muscle shortens, the force decreases, mechanical work is done, and ATP is hydrolyzed at a faster rate. However, skeletal muscle can also act as a brake to resist a sudden increase in load. When an active muscle is lengthened, the force increases (1), work is done on the muscle, and the rate of ATP hydrolysis decreases (2–4). The braking action of muscle is a matter of everyday experience, for example, when the extensor muscles of the legs have to oppose the momentum of the body when walking downstairs or landing at the end of a jump.

The molecular basis of the braking action of muscle is unknown. Muscle fibers become stiffer during a stretch (5), provided that the length change is distributed uniformly along the fiber (6–9), suggesting that force enhancement by stretch is related to the presence of an additional elastic structure. Because fiber stiffness during isometric contraction depends on myosin motors cross-linking the arrays of myosin and actin filaments in each muscle sarcomere, the stretch response might be due to recruitment of additional myosin motors. Alternatively, resistance to stretch could be due to other protein components; cytoskeletal proteins, for example, might become taut during the stretch. Whatever its molecular basis, the response must be activated during the stretch itself, i.e., on the millisecond timescale in the case of an extensor muscle during landing of the body after a jump. We therefore focused on the mechanical and structural changes in the muscle within the first few milliseconds after a rapid (120 μs) stretch imposed on an isolated intact muscle fiber during isometric contraction. Using a combination of x-ray and mechanical measurements, we show that such a stretch induces fast attachment of additional myosin motors to actin. The mechanism is related to the long established but previously unexplained fact that each molecule of muscle myosin contains two identical motor domains. During isometric contraction, only one of these motors is attached to actin and senses the applied stretch. Steric and mechanical coupling between the two motors leads to attachment of the second motor to actin to resist the stretch.

Results and Discussion

Mechanical Response to a Step Stretch.

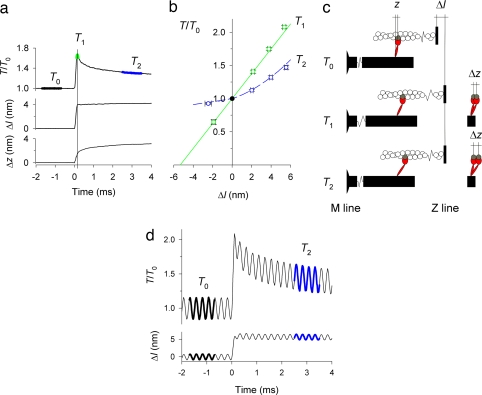
When a muscle fiber that has been activated at fixed length is suddenly stretched, the force increases during the stretch and then partially recovers in the next few milliseconds (Fig. 1a). The increase in force from the isometric value T₀ to the peak value T₁ during the stretch, which is called phase 1 of the force transient (10), corresponds to the undamped elasticity of the half-sarcomere, the effective functional unit joining the M line and Z line (Fig. 1c). This elasticity resides in the actin filaments, the myosin filaments, and the myosin head domains that cross-link them (11). The recovery of force from T₁ to T₂ in phase 2 (within the first 3–4 ms after the stretch) is due to reversal of the myosin motor stroke that drives muscle shortening (10, 12, 13).

Fig. 1.

Mechanical response to a step stretch imposed during isometric contraction. (a) Time course of force (T) relative to isometric force (T₀), length change of the half-sarcomere (Δl), and axial motion of myosin motors (Δz); time of x-ray exposures at T₀, T₁, and T₂ indicated on the force trace. (b) T₁ (green) and T₂ (blue) plotted against Δl (mean ± SEM, n = 19 fibers); data for shortening steps, here and elsewhere, are from ref. 25. The green straight line was obtained by regression of the T₁ data for ≈2-nm shortening and stretch steps and the isometric point (T₀, black circle); the blue dashed line was drawn through the T₂ points by eye. T₀ was 285 ± 90 kPa (mean ± SD). (c) (Left) Myosin motor (red) with its catalytic domain attached to a monomer (gray) in the actin filament (white) and light-chain domain (LCD) attached to the myosin filament backbone (black). Axial motion after a stretch is accompanied by tilting of the LCD and quantified by the axial separation z between the two ends of the LCD. (Right) Motor conformations at T₁ and T₂ superimposed on that at T₀. (d) Force response (upper trace) to a 5.7-nm stretch with superimposed 4-kHz oscillations (lower trace). Force and length oscillations used for the analysis are indicated by thickening of the traces. Black indicates T₀; blue indicates T₂.

The compliance of both the myosin and the actin filaments is 0.26%/T₀ (14–19), corresponding to a total filament compliance of 0.013 nm/kPa (20). T₀ is 285 kPa in the present experiments, and thus the contribution of the filaments to the compliance of the half-sarcomere is 3.7 nm/T₀. During a 3.8-nm stretch of the half-sarcomere, the force increases by 0.75 T₀ (Fig. 1a), and the increase in strain of the filaments is (0.75 × 3.7) or 2.8 nm. Thus, of the 3.8-nm stretch, only (3.8 − 2.8) or 1.0 nm is associated with the elastic distortion of the myosin motors (Δz). During the phase 2 recovery, after the 3.8-nm stretch, the force decreases by 0.43 T₀ (Fig. 1a), so the filaments shorten by (0.43 × 3.7) or 1.6 nm. The length of the half-sarcomere is almost constant during phase 2, so filament shortening takes place at the expense of additional distortion of the myosin motors (Δz) by 1.6 nm (Fig. 1 a and c).

Both T₁ and T₂ have a nonlinear dependence on the size of the stretch, Δl (Fig. 1b). The T₂ nonlinearity has been extensively characterized (10, 12, 13), whereas the smaller T₁ nonlinearity has received much less attention. The present results show that T₁ for large stretches is reproducibly above the straight line (Fig. 1b, green) obtained by linear regression of the data for small stretch or shortening steps and the isometric point (black circle). These results show that stiffness increases significantly during a large stretch. An increased stiffness 4 ms after a 4-nm stretch was reported in ref. 13. We measured stiffness after three sizes of stretch by imposing a small length oscillation at 4 kHz (Fig. 1d). With this protocol, the increased amplitude of the 4-kHz modulation of force indicates a 22% higher stiffness measured 3 ms after the stretch. The increase in stiffness after a stretch indicates either an intrinsic nonlinearity of the elasticity of the filaments or motors or the contribution of additional elastic structures recruited by the stretch. These could either be additional myosin motors or cytoskeletal proteins.

X-Ray Diffraction Changes After Step Stretch.

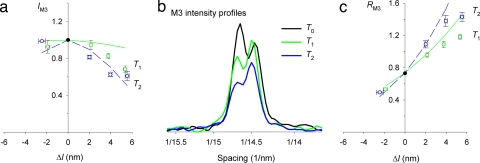
We investigated the contribution of myosin motors to the stretch-induced force and stiffness increase by x-ray interferometry, an in situ structural technique that can be applied to intact single muscle fibers with submillisecond time resolution. The regular 14.5-nm repeat of motors along the myosin filaments produces an x-ray reflection called the M3, the intensity of which (I_M3) depends on the number and mass distribution of the motors along the filament axis. I_M3 decreased during a step stretch (Fig. 2a, T₁, green circles) and decreased further during the phase 2 force recovery (T₂, blue circles). The width of the intensity distribution of the M3 reflection along the axis perpendicular to the muscle fiber was not affected by the stretch by >10%, as shown previously for releases (21), confirming that the I_M3 changes after a step are not influenced by changes in lateral filament alignment. The intensity profile of the M3 reflection along the axis parallel to the muscle fiber (Fig. 2b) is split into two major peaks by interference between x-rays diffracted by the two arrays of motors in each myosin filament (22). During isometric contraction, the ratio of the intensities of the higher and lower angle peaks (R_M3) is ≈0.75 (Fig. 2 b and c, T₀, black). R_M3 increases substantially during a step stretch (Fig. 2 b and c, T₁, green) and increases further during the phase-2 force recovery after a stretch (T₂, blue).

Fig. 2.

Structural response to step stretch. (a) Intensity of the M3 x-ray reflection (I_M3). Symbols are the same as in Fig. 1b. Lines are from the structural model in ref. 18. Green indicates T₁; blue indicates T₂. (b) Intensity profiles of M3 reflection along the meridional axis. Colors are the same as in Fig. 1. (c) Changes in the relative intensity of the two major peaks of the M3 reflection (R_M3). Symbols and lines are the same as in a.

These changes in I_M3 and R_M3 are due to stretch-induced structural changes in the actin-attached myosin motors. The decrease in I_M3 is caused by tilting of the motors, which broadens their mass distribution along the filament axis (21, 23, 24); the increase in R_M3 results from the increase in the interference distance between the two arrays of motors in each filament as they tilt away from the sarcomeric M line (18, 25) (Fig. 1c). This motion continues in the same direction during force recovery after the stretch (Figs. 1c and 2 a and c), as already inferred from the mechanical results as a cumulative change in motor distortion (Δz) during phases 1 and 2 of the stretch response (Fig. 1a). Structurally, this is signaled by both I_M3 (Fig. 2a) and R_M3 changes (Fig. 2c).

Asymmetry Between Structural Responses to Step Stretch and Release.

The mechanical analysis of stretch-induced motor distortion can be extended to the structural regime by using a simple model in which both the elasticity and working stroke of the motor are due to tilting of its light-chain domain (Fig. 1c), to calculate the expected values of I_M3 and R_M3 at T₁ and T₂ (25). The model parameters are further constrained by measurements of I_M3 and R_M3 during phase-2 shortening at constant load, conditions in which the effects of filament compliance are eliminated (18), effectively providing an in situ calibration of I_M3 and R_M3 in terms of the axial motion of the myosin motors. As for the shortening steps, this model fits the observed changes of I_M3 (Fig. 2a) and R_M3 (Fig. 2c) after the small stretch but clearly fails to reproduce the response to large stretches. The model generally underestimates the experimental changes in I_M3 (Fig. 2a) and overestimates those in R_M3 for large stretches (Fig. 2c).

The Second Myosin Motor Domains Attach Rapidly to Actin After a Stretch.

The discrepancies described above arise from the assumption that the number of actin-attached motors is constant, which is valid to a first approximation for shortening steps (20) and small stretches, but not for large stretches, as suggested by the mechanical data (Fig. 1 b and d). Although each molecule of muscle myosin has two motor domains, the low fraction of motors attached during isometric contraction [≤30%, or ≤88 of the 294 motors present in each myosin half-filament (20, 26–28)] makes it likely that most myosins are attached to actin by a single motor domain. We propose that a step stretch induces rapid attachment of the second motor domain of some of these myosin molecules and that this is responsible for the braking action of muscle.

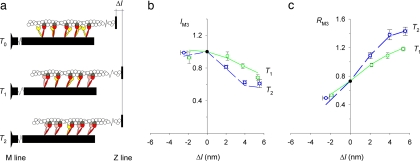
The details of the proposed mechanism are diagrammed in Fig. 3a, which for simplicity shows only myosins that have at least one motor domain attached to actin. During isometric contraction (Fig. 3a Top, T₀), the red motors are attached to actin, and their partners (yellow) in the same myosin molecule are detached, with greater axial disorder. By the end of phase 1 (Fig. 3a Middle, T₁), some of the partner motors (pink) have attached to the adjacent monomer (light gray) closer to the M line, and this process continues during phase 2 (Fig. 3a Bottom, T₂). This model reproduced the observed values of both I_M3 (Fig. 3b) and R_M3 (Fig. 3c) after a stretch, both at T₁ (solid green line) and T₂ (dashed blue line). The details of the modeling are described in supporting information (SI). Two features of the model were shown to be essential to reproduce the experimental x-ray data. First, the newly attached motors must be displaced M-wards with respect to those attached during isometric contraction (Fig. 3a); without this constraint, the new attachments increase the discrepancy between the calculated and observed values of I_M3 after a stretch, and the observed saturation of the R_M3 response to larger stretches cannot be reproduced. Second, there are two populations of detached motors with different axial dispersions during isometric contraction, and the additional attachments promoted by a stretch come from the population with lower axial dispersion; without this constraint, the progressive reduction of I_M3 during stretches of increasing size cannot be reproduced. Both of these features are simply explained by the partner motor hypothesis.

Fig. 3.

Structural model including stretch-induced attachment of myosin motors. (a) Structural model of motors and filaments modified from Fig. 1c. Red indicates motors attached to actin monomers (dark gray) at T₀, yellow indicates detached partner motors, and pink indicates partner motors attached to the next actin monomer on the M-ward side (light gray). (b and c) I_M3 (b) and R_M3 (c) data from Fig. 2 a and c, respectively. Lines are from the model with the stretch-induced attachment described in the text. Symbol and color codes are as in Fig. 2a.

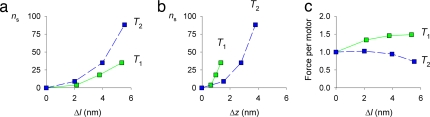
The number of motors attached to actin (n_s), as determined by fitting the data in Fig. 3, continues to increase during the phase-2 force recovery after a stretch (Fig. 4a). Eighty-eight new motors had attached to actin at the end of phase 2 after a 5.3-nm stretch (Fig. 4a, blue), the same as the number already attached during isometric contraction at T₀ (20, 28). The increase in n_s during phase 2 is as large as that during the stretch itself. This behavior also follows naturally from the partner head attachment model, in which the continuing increase in motor distortion (Δz) during phase 2 (Fig. 1 a and c) is expected to further increase the probability of attachment of the partner motor to the next M-ward actin by a simple steric mechanism. These results demonstrate that active muscle resists a sudden increase in load by recruitment of new myosin motors triggered by the distortion of the motors that were attached to actin during isometric contraction.

Fig. 4.

Number (n_s) of additional myosin motors attached to actin after a stretch and the force per motor. (a) n_s plotted against stretch size (Δl). (b) n_s plotted against axial motion of motors (Δz). (c) Average force per myosin motor plotted against Δl. Green indicates T₁; blue indicates T₂.

The steric mechanism described above does not completely determine the extent of recruitment of new motors. For a given value of motor distortion Δz, n_s is larger at T₁ than at T₂ (Fig. 4b). It is therefore likely that the elastic strain in the attached motor, which is larger at T₁ than at T₂, also plays a role in promoting attachment of new motors. These results provide further support for the proposal that the newly attaching motors are the partners of those already attached to actin during isometric contraction (Fig. 3a). The partner motors are mechanically coupled by their shared attachment to the myosin tail; the attached motor is the strain sensor that rapidly detects an external stretch, and the mechanical link between the two motors in one molecule constitutes the signaling pathway that controls rapid attachment of the second motor.

Mechanics and X-Ray Diffraction Give Similar Estimates of Motor Recruitment.

The number of additional myosin motors attaching to actin during a stretch can be estimated independently from the difference between the observed T₁ relation (circles in Fig. 1b) and the line corresponding to the stiffness of the half-sarcomere during isometric contraction (green line in Fig. 1b). The details of the calculations are presented in SI. The resulting increase in the stiffness of the array of motors attached to actin in each half-sarcomere was 23% and 32% for stretches of 3.8 and 5.3 nm, respectively, corresponding to attachment of 20 and 28 new motors in each myosin half-filament.

The stiffness of the motors at the end of the quick force recovery (T₂) can be calculated from the synchronous 4-kHz force and length changes during the time window used for the x-ray measurements (Fig. 1d). Again stiffness increased with stretch size (see SI), indicating attachment of 17, 62, and 78 additional motors at T₂ for stretches of 2, 4, and 5.7 nm, respectively.

The general agreement between the mechanical and x-ray estimates (Fig. 4a) of the number of newly attached myosin motors demonstrates that the increase in stiffness elicited by stretches of 2–6 nm is not due to an increase in the stiffness of any element contributing to half-sarcomere elasticity (actin filament, myosin filament, or individual myosin motors) or to recruitment of a parallel elasticity in another structural component. The finding that the stiffness of the individual myosin motor is the same for stretches and step releases also indicates that the compliant structural element in the myosin motor (29) has the same elastic properties when it acts as a motor and as a brake.

The Second Motor Domain of Skeletal Muscle Myosin Limits the Force per Motor Under Stretch.

The average force per motor can be calculated as the total force per filament divided by the number of attached motors per filament (Fig. 4c). It is notable that by the end of phase 2, when the force per filament is up to 1.5 times greater than that during isometric contraction (Fig. 1b, blue), the force per motor is never greater than that during isometric contraction (Fig. 4c, blue). Attachment of partner motors acts in a fast negative feedback loop to resist external forces of twice the isometric force while minimizing the stress on an individual motor.

Many members of the myosin family have two motor domains. For some myosins, such as myosin V, the function of the two domains is clear. Single molecules of myosin V travel for large distances along an actin filament via a processive motion, and at any time at least one of the motors is attached to actin (30, 31). Muscle myosin II is not processive, and the functional significance of its dimeric structure was previously unknown. The present results show that the dimeric structure is essential for the braking action of skeletal muscle, allowing muscle to rapidly detect and resist an external stretch. A similar mechanism, operating on a slower time scale, was recently proposed for nonmuscle myosin II (32). Thus, coupling between the two motors in dimeric myosins has a broader functional role than was previously appreciated.

Methods

All experiments were performed at the ID02 beamline of the European Synchrotron Radiation Facility on single intact fibers from the skeletal muscle of the frog (Rana temporaria). Frogs were cooled to 2–4°C and killed by decapitation followed by destruction of the brain and spinal cord in conformation with European Union Directive 86/609/EEC and the U.K. (Scientific Procedures) Act of 1995. Single fibers, dissected from the lateral head of the tibialis anterior muscle, were transferred to an experimental chamber containing Ringer's solution [115 mM NaCl, 2.5 mM KCl, 1.8 mM CaCl₂, and 3 mM phosphate buffer (pH 7.1)] and mounted at sarcomere length 2.1 μm between a capacitance force transducer and loudspeaker-coil motor by means of aluminum foil clips to minimize the compliance of tendon attachments (6). The temperature of the bathing solution was set to 4°C by feedback to a thermoelectric module.

Mechanical Protocol.

The mechanical protocol was first tested using a striation follower (33) that measured the sarcomere length in a 1- to 1.5-mm segment of the fiber continuously during the contraction with 5-μs time resolution. The fiber and mechanical apparatus were then mounted vertically on the x-ray beamline, and the same mechanical protocols were repeated in combination with x-ray measurements. Fibers were electrically stimulated at 4-min intervals for periods of 0.5–1.35 s, with a stimulus frequency of 18–25 Hz. After 0.35 s of isometric contraction, when force had attained the isometric tetanus plateau (T₀), 5–50 stretch/shortening cycles of 20-ms periods were imposed on the fiber. Each cycle consisted of a stretch, followed after 4 ms by a release of the same size; the cycle was repeated after 16 ms, a time long enough to ensure that the repriming of the force response is complete and that the response to each stretch in the train is the same as that to the first stretch (24). Stretches larger than 6 nm per half-sarcomere were not used because they induce fast detachment of the myosin motors attached to actin in isometric contraction (13). A total of 19 muscle fibers with a cross-sectional area of 22,400 ± 6,600 μm² (mean ± SD) and an isometric force (T₀) of 285 ± 90 kPa were used. In one experiment, before mounting on the x-ray beamline, the stiffness of the active fiber before and after 2- to 6-nm stretches was determined by imposing small length oscillations at 4 kHz. The mechanical responses in two 1-ms time windows (Fig. 1d), corresponding to the two time windows of x-ray exposure at T₀ and at T₂ (Fig. 1a), were analyzed by means of the fast Fourier transform (FFT) routine provided by LabVIEW software (National Instruments) to estimate the in-phase and quadrature stiffness.

X-Ray Data Collection and Analysis.

The x-ray path in the physiological solution surrounding the fiber was minimized by two moveable mica windows 600 μm apart on either side of the fiber that also carried the platinum wire electrodes for electrical stimulation of the fiber. The x-ray beam had a FWHM of ≈0.1 mm vertically and 0.3 mm horizontally; the flux at the fiber was ≈2.10¹³ photons per s, and the wavelength was 0.1 nm. The x-ray diffraction patterns were recorded with a FReLoN CCD detector with image intensifier, placed at 10 m from the fiber. Data were corrected for dark current, flat field, and spatial distortion as described by Narayanan et al. (34). The 2,048 × 2,048 pixels of the CCD were binned by factors of 2 in the axial direction, parallel to the fiber axis, and by 16 in the radial direction before the readout. The axial point spread function of the detector had a FWHM of 250 μm.

X-ray exposure was controlled using two electromagnetic shutters in tandem and was monitored with 10-μs resolution using a pin diode. Radiation damage of the fiber was minimized by translating the fiber vertically by ≈100 μm between x-ray exposures, and data could typically be collected from ≈40 activations without effect on fiber function.

X-ray data were recorded during the isometric period just preceding the step stretch (T₀), at the end of phase 1 of the response to the step stretch (T₁), and at the end of the quick force recovery after the step stretch (T₂) (Fig. 1a). To isolate the short-lived transient conformations generated by the step stretch, x-ray exposure was limited to 100 μs for the T₁ response (from 90 to 190 μs after the start of the step, green) and to 1 ms for the T₂ response (from 2.5 to 3.5 ms after the step stretch, blue). The time exposure for T₀ was also 1 ms (from 1.7 to 0.7 ms before the step stretch, black). For each tetanus, data for only one of the three time windows were accumulated on the CCD from a series of stretch/release cycles (24). To achieve the total x-ray exposure of 5 ms per tetanus required for adequate signal-to-noise ratio, T₁ time frames (100 μs) were added from 50 cycles, and T₂ and T₀ time frames (1 ms) were added from 5 cycles. The first stretch–release cycle started 0.35 s after the first stimulus, and the tetanus duration was adapted to the number of cycles in the train: 1.35 s for 50 cycles and 0.5 s for 5 cycles, as in the contractions used for sarcomere length measurements. X-ray data were also recorded using the acquisition protocols described above but in the absence of imposed length steps and in a single 5-ms window in isometric tetani. There were no significant differences between these data and those acquired in a series of five 1-ms windows in the isometric periods preceding a stretch.

The distribution of diffracted intensity along the vertical axis of the x-ray pattern, parallel to the muscle fiber axis, was calculated by integrating the 2D data from 0.012 nm⁻¹ on either side of the axis. Background intensity was subtracted after straight-line or smooth-convex hull fitting. The interference components of the M3 reflection during the three different phases of the contraction (T₀, T₁, and T₂) were extracted by fitting multiple Gaussian peaks to the axial intensity distribution under the constraint that they had the same axial width, and the total intensity of the reflection was calculated as the sum of the component peaks. The spacing of each reflection was determined from the weighted mean of the component peaks and was calibrated by that of the M3 reflection in the isometric tetanus, 14.573 nm (22). X-ray data were analyzed using the software packages Fit2D (provided by A. Hammersley, European Synchrotron Radiation Facility) and Peakfit (SPSS Science).