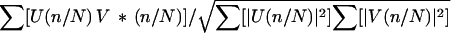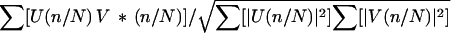Figure 4.

In the heavily overdamped environment of an optically trapped bead, the equation of motion is F_u(t) − αu(t) − b du(t)/dt + [w(t) − u(t)]γ_u = 0, where F_u(t) refers to thermal forces upon the bead, α is trap stiffness, u(t) refers to bead position relative to trap position, b is the coefficient of viscous drag, w(t) is the position of the myosin-binding site on the actin filament relative to its equilibrium value, and γ_u is the stiffness of the bead/actin connection. A similar equation governs movement of the second bead with position v(t). A third equation reflects balance of tension among the compliant bead/actin connections and the surface myosin connection. [w(t) − v(t)]γ_v + [w(t) − u(t)]γ_u + Mw(t) = 0, where γ_v is the stiffness of the bead/actin connection at the end of the actin filament corresponding to v(t) and M is the stiffness of the linkage between the surface and the actin filament, through a single myosin molecule. After using the third equation to eliminate w(t) from the first two, we Fourier transform and solve for U(f) and V(f), each in terms of F_u(f) and F_v(f). These resulting equations are linear with complex, frequency-dependent coefficients. We wish to compute the correlation coefficient between sampled signals u(n) and v(n) reflecting u(t) and v(t) in the time domain. We can compute the Discrete Fourier Transform U(n/N) and V(n/N) by sampling the continuous U(f) and V(f) at fine intervals and extending this by symmetry. Using Parseval’s Theorem, we relate the linear correlation coefficient between u(n) and v(n) to the Discrete Fourier Transform

The latter expression can be expanded in terms of F_u(n/N) and F_v(n/N). Because thermal forces acting upon the two beads cannot be correlated, cross-terms like Σ[F_u*(n/N) F_v(n/N)] can be dropped. Moreover, because the pattern of heated water molecule collisions with the beads changes faster than all relevant time scales here, F_u(n/N) and F_v(n/N) at every frequency are both equal on average to the same constant, and thus they cancel. The resulting expression is a complex sum over digital frequency involving only known parameters, aside from γ_u, γ_v, and M. In the upper graph, we set M = 0. The diffusion correlation coefficient now depends on γ_u and γ_v only through a series combination of the two, as expected. The solid line is computed with a solution viscous drag coefficient of 9.42∗10⁻⁶ g/s. The dotted line is computed with a coefficient twice this value, to account roughly for surface proximity effects on Stoke’s Law. As shown, the mapping of stiffness-to-diffusion correlation coefficient does not depend sensitively on the drag coefficient, so surface proximity effects are not significant. The fine, straight lines map the measured diffusion correlation coefficient of 0.45 to a predicted bead-to-bead stiffness of 0.025 pN/nm, which can be compared with the 0.027 pN/nm expected on the basis of position variance measurements. In the lower graph, we use the γ_u and γ_v measured by position variance and allow M to vary between 0 and 1 pN/nm. Inset is an expanded area of the marked section on the plot of diffusion correlation coefficient versus M (pN/nm). The fine, straight lines in the Inset map the center of the measured diffusion correlation coefficient distribution to 0.65 pN/nm and the extrema of the error range (uncertainty, 0.01; see Fig. 3 legend) to 0.53 and 0.83 pN/nm.