Figure 3.
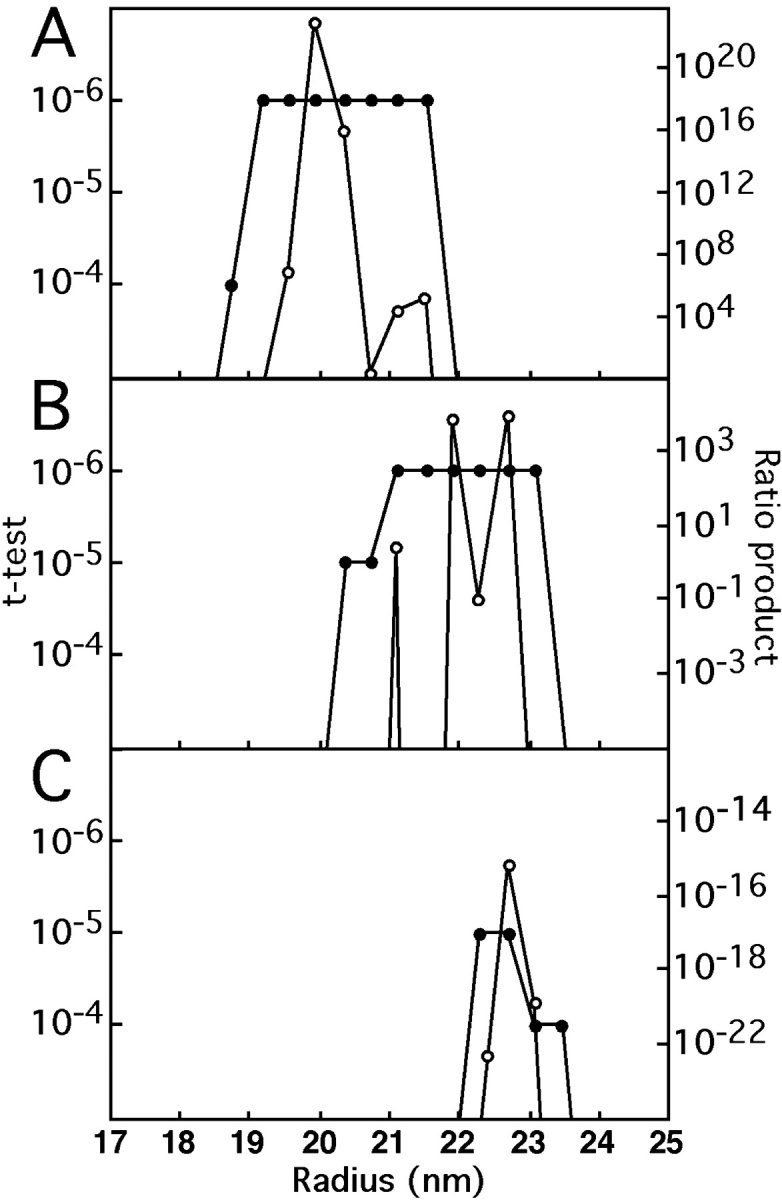
Detection of rotational symmetries in RTTs as a function of radius. Two measures of significance, Student's t test and the ratio product (Kocsis et al. 1995), were applied to two subsets of images, comprising 167 smaller rings and 256 larger rings, respectively. For polar-sampled images, the t test assesses at each radius and for each potential order of symmetry, whether that symmetry is significantly represented in the data set as a whole. The only significant symmetries detected were 28-fold (A) in the smaller set, and 30-fold (B), and 32-fold (C) in the larger set. For instance, in A, 28-fold symmetry is detected at the P < 10−6 level at radii of 18–22 nm. N-fold symmetry at radius R corresponds to an azimuthal spacing of 2πR/N in the specimen. For a given candidate symmetry at a given radius, the ratio product is the product of the corresponding Fourier amplitudes from all the images, normalized against the average amplitude from the background images. This product converges rapidly to zero except when a certain symmetry is significantly present. The relative proportions of particles with different symmetries may be estimated from the product ratios when both saturate the t test–calculated limit of P < 10−6. In this case, it may be estimated that 30-fold rings are three- to fourfold more abundant in the large subset than are 32-fold rings.
