Sexual reproduction prevails in a world of structured resources in short supply

Abstract

We present a model for the maintenance of sexual reproduction based on the availability of resources, which is the strongest factor determining the growth of populations. The model compares completely asexual species to species that switch between asexual and sexual reproduction (sexual species). Key features of the model are that sexual reproduction sets in when resources become scarce, and that at a given place only a few genotypes can be present at the same time. We show that under a wide range of conditions the sexual species outcompete the asexual ones. The asexual species win only when survival conditions are harsh and death rates are high, or when resources are so little structured or consumer genotypes are so manifold that all resources are exploited to the same extent. These conditions, largely represent the conditions in which sexuals predominate over asexuals in the field.

1. Introduction

The question of why most species reproduce sexually despite the ‘twofold cost of males’ is one of the most discussed but not yet satisfactorily answered ones in evolutionary biology (West et al. 1999). Explanations range from the ability of sexual species to evade parasites or predators (the Red Queen hypothesis; Hamilton 1980; Otto & Nuismer 2004) and the advantage of producing genetically different offspring in a capricious or heterogeneous environment (the lottery model and the tangled bank hypothesis; Williams 1975; Bell 1982) to avoid the accumulation of deleterious mutations (Muller's ratchet; Muller 1964; Keightley & Otto 2006).

While all these effects may have played a role in the evolution and maintenance of sexual reproduction, we focus here our attention on the role of resource availability in determining the mode of reproduction. The availability of resources is the strongest factor affecting the growth of populations, and the mode of reproduction that allows for a better use of the resources should therefore dominate. This is the main ingredient of the tangled bank models mentioned above (Bell 1982; Case & Taper 1986) and of closely related species competition models (Pound et al. 2002). In these models, sexual species have a larger niche width than asexual clones and can therefore exploit a wider range of resources if the environment is heterogeneous. Tangled bank models typically lead to the coexistence of sexual species with an asexual clone. The sexual species cannot completely displace an asexual clone owing to its larger growth rate. If several asexual clones are present, they can displace the sexual species if they can together exploit the same range of resources as the sexual species. The persistence of sexual reproduction in tangled bank models is therefore dependent on a rare production and an eventual extinction of asexual clones.

In this paper, we suggest a model different from conventional tangled bank models and with larger explanatory power. This model predicts that sexual species outcompete asexual species under a wide range of conditions. Like the tangled bank models, our model assumes that there exists a broad spectrum of resources that cannot all be exploited by one genotype. Indeed, experiments show that genetically diverse populations can better exploit resources than genetically homogeneous populations (Doncaster et al. 2000). The model contains three key features that are crucial to the outcome. First, the timing of sexual reproduction depends on the scarceness of resources. Second, resources that have been exploited in one season will not be available to the same extent or of the same quality in the next season, and third, locally only a few genotypes can be present at the same time.

The first feature is characteristic of species that can switch between the two modes of reproduction. For instance, phytophagous insects (Normark 2003) and aquatic filter feeders, such as water fleas and monogonont rotifers (King 1980), grow and reproduce asexually on their food resources until they become limiting and then produce offspring sexually, which disperse and start a new asexual cycle in the next season. Reviewing parthenogenetic reproduction in the animal kingdom and in the protists, Bell (1982, 1988) concluded that the best predictor of the initiation of sexual reproduction in species with intermittent mixes is scarcity of resources. There thus is ample evidence that resource availability determines the timing of sexual reproduction.

The second requirement mentioned above for our model is that resources grow slowly or regrow in a different way and therefore are not present to the same extent or in the same form for the consumers of the next generation. For the consumer–resource pairs that inspired our model, such as herbivore insects and plants or parasites and hosts, this requirement is fulfilled because the generation time of the resource is often much larger than the generation time of the consumer. Furthermore, exploited resource individuals and populations may change chemically or anatomically due to induced defence which usually persists over a considerable time span during which the consumer can use this resource less or not at all (Dicke & Hilker 2003; Laforsch & Tollrian 2004). We would like to point out that all these mechanisms are different from lottery models (Williams 1975; Bell 1982), where resources vanish completely, and different (new) resources appear stochastically. In our model, the same set of resources is present all the time, but availability changes are dependent on consumption.

The third feature of our model is that locally only a few genotypes can be present at the same time. This is the case in r-selected species, such as many insects and aquatic species with planktonic larval phase, where the number of individuals present in the next generation is determined predominantly by abiotic density-independent factors and by predation on early developmental stages, i.e. is essentially independent of the number of eggs deposited by the previous generation (Chesson 1998). It is important to realize that the mentioned factors determining the number of genotypes that are locally present are independent of the resources. The number of these genotypes is therefore much smaller than the number of genotypes that would be needed to cover the entire spectrum of resources if this spectrum is broad. If there could be enough genotypes present to cover the entire spectrum of resources, a sufficient number of asexually reproducing clones would be as effective at consuming the resources as the same number of sexual genotypes. However, if the number of genotypes is less than needed to cover the entire spectrum of resources asexually reproducing consumers have a disadvantage. They have offspring that are genetically identical to the parent generation and that will again exploit the same resources in exactly the same way. In contrast, the offspring of sexually reproducing consumers can exploit the resources in a different way and can therefore use a part of the resources that has not been used by the parent generation.

2. Model

Resources are arranged in a two-dimensional trait space with trait values ranging from 1 to L in both dimensions. For L=20, which is the value we used often, there are 400 different types of resources. The trait space of the consumers is also two-dimensional and is scaled such that the resource which can be consumed best is the one that has the same trait values as the consumer. Therefore, the consumer trait values also range from 1 to L in both dimensions. There are as many possible consumer genotypes as the resource types.

The dynamics of resource and consumer populations is divided into two stages. First, there is the stage of rapid asexual consumer growth and fast resource consumption, until consumer growth rates become negative because resources become limiting. Then sexual consumers mate and the offspring genotypes which start the growth cycle in the next season are calculated. Resources recover partially until the beginning of the next season.

The consumer growth stage is described by the following set of equations:

$${\dot{P}}_j=f\sum _i{a}_{ji}{P}_j{R}_i-\text{d}{P}_j,$$

$${\dot{R}}_i=-\sum _j{a}_{ji}{P}_j{R}_i,$$ (2.1)

where P_j denotes the biomass of consumer number j (characterized by a genotype (x_j, y_j)) and R_i the biomass of resource number i (with trait values x_i, y_i). The ecological efficiency f had the value 0.2 in all our simulations (Stephens & Krebs 1986). d is the death rate, and the coupling a_ji is given by

$$a_{ji}=a_0{\text{e}}^{-\alpha |i-j{|}^2},$$

where |i−j| denotes the Euclidean distance between genotype i and genotype j in the two-dimensional genotype space, and α⁻¹ is a measure of the range over which a species can take resources. Consumers can exploit best the resource that agrees with their own genotype, but they can also use to some extent neighbouring resources. In our simulations, we chose a₀=α=1. Every consumer grows until the growth rate drops below zero. Then the growth of this consumer ends. When all consumers have finished growing, the starting configuration for the next season or the next generation is calculated.

The resources recover partially until the beginning of the next season according to the equation

$$\mathrm{\Delta }{R}_i=G(1-R_i/R_{\text{max}}),$$ (2.2)

with constants R_max and G≤R_max that were for simplicity chosen identical for all resources, which means that the edge in resource space is abrupt. R_max is the maximum resource biomass and G the maximum amount by which the resource can grow from one season to the next.

The number of consumer individuals that start the new generation (with population size one each) is determined by factors other than the resources. We assume therefore that each of the eggs laid has the same chance of giving rise to an adult individual in the next generation, and that the number of consumer individuals that start the new generation is of the same order of magnitude each time. Since the number of eggs is much larger than the number of individuals surviving to the reproduction stage, and since the product of the number of eggs and the survival probability is roughly the same in each generation, we choose the number of consumer individuals from a Poisson distribution with a mean value n, which is another model parameter. The genotypes of the individuals starting the new generation are determined in the following way. For each individual, we first decided whether it will be sexual or asexual. It is sexual with probability

$$p_{\text{s}}=\frac{{\sum }_{j\text{sexual}}{P}_j}{{\sum }_{j\text{sexual}}{P}_j+2{\sum }_{j\text{asexual}}{P}_j},$$ (2.3)

and asexual otherwise. This means that asexuals have laid twice as many eggs per individual as sexuals, because half of the sexual individuals are males. The genotype of an asexual individual is chosen at random among the genotypes of all asexual individuals of the previous generation, with weights proportional to the population sizes. This means that every egg laid by asexuals has the same chance of giving rise to an adult individual of the next generation. If a considerable proportion of eggs have the same genotype, several of the individuals starting the new generation may also have the same genotype. The genotype of a sexual individual is determined by choosing at random two parent individuals among all sexual individuals at the end of the previous generation, and by assigning to the offspring a genotype chosen from a (discretized) Gauss distribution of variance V_g (chosen to be 1) around the midparent value in both dimensions of genotype space. This means that every sexual individual at the end of the previous generation has the same chance of becoming the parent of an individual in the new generation.

Finally, there is a small probability (chosen to be 1%) that a sexually produced individual is asexual. This ingredient of the model allows sexuals to win only if they cannot be invaded by asexuals. It implements Vrijenhoek's (1979) ‘frozen niche hypothesis’ that asexual clones arise in a sexual population with genotypes frozen to those of the progenitor parent.

3. Results

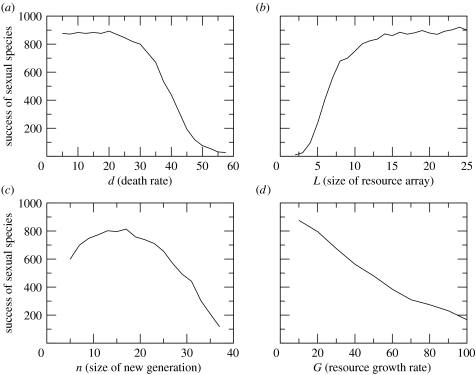
The model is initiated with all R_i=R_max (chosen to be 100) and with randomly chosen consumer genotypes, each of them being sexual or asexual with probability 0.5. The simulation continues until there are only sexual or only asexual individuals left. We did 1000 runs for the same values of the parameters and recorded how often the asexuals and sexuals won. The sexuals usually do not win in 100 per cent of the simulations because there is a non-vanishing probability that initially there are no or almost no sexuals, in which case the asexuals are likely to win. The simulation lasted typically a few generations, usually in the two-digit range. We varied the four parameters d, L, G and n and plotted the results in figure 1. The results can be readily understood: whenever sexual individuals can exploit new, unused resources, they have an advantage over the asexual ones and win the majority of the simulation runs. This advantage vanishes in the following situations: (i) when the death rate is so large that hardly any resources are consumed. In this case there is no advantage in taking a new resource compared to taking the same resource as in the last season, (ii) when the number of different resources is so small, or (iii) the number of genotypes is so large that all possible resources are exploited to the same extent. This happens when L is small and when n is large, (iv) when resources recover so fast that they are fully regrown at the beginning of the next season. In this case there is again no advantage in switching to different resources. (The decline of sexuals for small n is due to the fact that the initial number of sexual consumer individuals can be very small due to statistical fluctuations.)

Figure 1.

Number of times (out of 1000) the sexuals won as function of the parameters (a) d, (b) L, (c) n and (d) G. In simulations where these parameters are not varied, their values were chosen to be L=10 (only for varying n, where larger L require too long simulation times), d=5, G=10, and n=10.

We performed our simulations also with different values of the parameters and the results were essentially the same. This means that the results are robust features of the model.

In order to obtain an idea of the breadth of genotype or trait values present in the winning mode of reproduction, we evaluated the variance $\overline{x^2}-{\overline{x}}^2+\overline{y^2}-{\overline{y}}^2$ of the winning species and averaged over all runs (out of 50 000) where the same mode of reproduction won. We only counted runs where it took more than 10 seasons before a mode of reproduction won. The results for varying parameter d are shown in figure 2. The variance of the winning species decreases with increasing d both for sexuals and for asexuals. We ascribe this decrease to the fact that for larger d survival is more difficult and therefore fewer genotypes are present. The decrease of the asexual variance is initially steeper, and the two curves cross at a value of d where the sexuals still win most of the runs. We conclude that for small d, where the advantage of sexuals is largest, the asexuals can only win if they succeed in maintaining a particularly large genetic variance, while for large d the sexuals can win if they succeed in maintaining a genetic variance somewhat larger than that of asexuals.

Figure 2.

Variance in trait value of the winning mode of reproduction for the simulations shown in the first graph of figure 1. plus, asexuals; cross, sexuals.

4. Discussion

We have presented a model that applies to species that multiply asexually during the season and that lay eggs which survive conditions when resources are vanishing during winter or periods of drought. The eggs may be produced sexually or asexually. This scenario applies not only to taxa which alternate between sexual and parthenogenetic reproduction (intermittent mixes) such as cladocerans (Hebert et al. 1993; Hebert & Finston 2001), monogonont rotifers (King 1980) and aphids (Simon et al. 2002; Halkett et al. 2004), but also to other groups with multiple parthenogenetic generations per season and potentially competing sexual and parthenogenetic lineages such as cecidomyiid dipterans (Suomalainen et al. 1987), collembolans (Chahartaghi et al. 2006), millipedes (Enghoff 1994; Jensen et al. 2002), isopods (Fussey & Sutton 1981; Fussey 1984), oribatid mites (Palmer & Norton 1991; Cianciolo & Norton 2006), gastropods (Jokela et al. 1997; Neiman et al. 2005), earthworms (Jaenike & Selander 1979; Viktorov 1997), enchytraeids (Christensen 1980; Christensen et al. 2002), nematodes (Cable 1971; Tirantaphyllou & Hirschmann 1980) and flatworms (Weinzierl et al. 1999; D'Souza et al. 2004). The advantage of sexual reproduction at the end of the season consists in being able to use different resources in the next season. The twofold cost of sex due to producing males is incurred only once per season. We found that over a wide range of parameters the sexual species displace completely the asexual species in the majority of cases. The parameter ranges where asexuals tend to win are when death rates are high; when resources are little structured or when they are replenished fast; or when a sufficient number of clones can persist that cover the entire spectrum of resources.

As stated above the model applies to taxa with intermittent mixes such as cladocerans and aphids. In aphids, however, only sexuals lay cold-resistant eggs, while asexuals produce offspring by vivipary. All species reproduce parthenogenetically during the season, but the sexual species can produce sexual, egg-laying offspring some time in fall. Since the production of cold-resistant eggs is coupled to sexual reproduction, sexual reproduction is maintained due to the harshness of at least some winters (Simon et al. 2002; Halkett et al. 2004). However, this does not explain why the production of eggs came to be coupled with sexual reproduction in the first place. Here, our model might give an explanation: it predicts that egg-laying asexuals would be outcompeted (or possibly have been outcompeted in the past) by egg-laying sexuals. Fitting with this scenario there still exist some primitive lineages of aphids, Adelgidae and Pylloxeridae, also producing eggs parthenogenetically (Simon et al. 2002).

Although the model was tailored to describe the life cycle of seasonally parthenogenetic species, we believe that the ideas underlying the model and the conclusions resulting from it range much farther. Indeed, the three key features of the model characterize, in modified form, many other species. Certainly, all multicellular organisms alternate between phases of asexual growth (growth in body size and asexual reproduction; Hughes 1989) and a stage of sexual reproduction producing offspring that is genetically different from its parents. Of course, the type of equation characterizing the growth process can be different in different types of species. Furthermore, it appears that the number of asexual reproductive events between sexual reproductive events depends on the amount of food available. This holds also for large animals, where individuals are smaller and may reproduce earlier in environments where food is scarce (Begon et al. 2005). Interestingly, in unitary organisms (cf. Begon et al. 2005) the onset of sexual reproduction coincides with the termination of somatic cell proliferation (growth). One might conclude that scarcity of resources must also have been a driving factor for the evolution of sexual reproduction. In large animals as well as in the types of species discussed in this paper, sexual reproduction is organized such that the new generation starts feeding at a time of (relative) plentiness of food.

The second key feature, that resources are not available in the same form for the consumers of the next generation, seems also to be rather universal. When the predator is much larger than the prey and when the prey has a shorter generation time, prey genotypes suffering from severe predation will have less offspring than other genotypes and will therefore need several generations to recover.

The third key feature, that locally only a few genotypes can be present at the same time, is also true for territorial species, such as many vertebrates. Here, the number of successful recruits in the following generation essentially relies on the death rate of the previous generation rather than on the number of offspring produced (Begon et al. 2005). More generally, considering that sexual populations consist of a vast number of genotypes with presumed differences in resource utilization spread over the whole range of the species, it is obvious that locally only a small fraction of these genotypes can be present.

Clearly, the details of the model would be different for each system considered but the outcome should be similar. Indeed, the four scenarios for which the asexuals win correspond generally well to those where asexuals occur in nature. Cases (i) (large death rate) and (iv) (little resource exploitation) correspond to the situation at the limits of the range of species where survival is hard and driven in large by density-independent factors rather than by the amount of available food resources which recover quickly from consumption (DeAngelis & Waterhouse 1987). In fact, the puzzling situation of geographical parthenogenesis (Peck et al. 1998) where parthenogenetic lineages dominate at boundaries of ranges (Hebert & Finston 2001) fits this scenario, as has been proposed early by Glesener & Tilman (1978) in an intuitive way. Furthermore, the scenario may explain why there are many parthenogenetic species in harsh environments, such as deserts (Kearney 2003) and ephemeral habitats colonized e.g. by bdelloid rotifers, the most famous group of parthenogenetic multicellular animals (Mark Welch & Meselson 2000). High mortality or slow growth of resources implies also that there is less asexual growth between two sexual reproductions, increasing the average cost of males per generation. Despite this increased cost, the advantage of sexuals increases when resources grow slower. Case (ii) (narrow resource spectrum) may explain why asexual reproduction is so widespread in soil, where the available food is detritus, which is consumed by a large number of primary decomposers, including fungi, micro- meso- and macrofauna species. Each of these groups consists of a substantial number of asexual or parthenogenetic species. Decomposer fungi in litter materials typically are dominated by imperfect species with infrequent or entirely lacking sexual stages (Dix & Webster 1995). In the most abundant soil protists, flagellates, naked and testate amoeba, sexual processes are unknown (Bell 1988). In soil decomposer invertebrates, virtually any larger taxon contains various parthenogenetic species, e.g. in earthworms (Terhivuo & Saura 1996), isopods (Christensen et al. 1987) and collembolans (Chahartaghi et al. 2006); the most striking group being oribatid mites with an estimated 10% of all species reproducing via parthenogenesis (Palmer & Norton 1992; Maraun et al. 2003; Heethoff et al. 2007). The large numbers of parthenogenetically reproducing decomposer species, all of which ingest the same resource, suggests that they extract different types of nutrients from the resource, which is indeed confirmed by recent studies based on stable isotope and fatty acid analyses (Schneider et al. 2004; Ruess et al. 2005; Chaharthagi et al. 2006). Such complications are not included in our model. Case (iii) (many consumer genotypes at the same place) may apply to saprophytic as well as arbuscular mycorrhizal fungi. Owing to parasexual processes in imperfect fungi (Ascomycota; Pontecorvo 1956), the number of genotypes is likely to match the number of resources exploited (different types of dead organic matter). A similar scenario may apply to arbuscular mycorrhizal fungi living on (uniform) carbon resources provided by plant roots (Gandolfi et al. 2003).

The major advantage of sexuality according to our model is the production of offspring able to exploit additional resources in a local community. Indeed, sexual processes such as outcrossing are abandoned in favour of inbreeding and parthenogenesis if resources are in ample supply (Hamilton 1967, 1993; Bell 1982; Knowlton & Jackson 1993), in agreement with situation (iv) for our model. The recent discovery of ant colonies consisting of parthenogenetically produced queens but sexually produced workers also support the view that sexual reproduction allows a more efficient exploitation of local resources (Pearcy et al. 2004). Further support for our model comes from studies suggesting that the invasion of local communities by genetically diverse invaders is more successful indicating that they are more successful in exploiting limited resources (Doncaster et al. 2000; Tagg et al. 2005). Therefore, the advantage of sex is most likely to occur if different genotypes, e.g. of different geographical regions, are blended. In fact, outcrossing is one of the most striking but also most puzzling phenomena of sexual reproduction since it results in the break-up of locally adapted genotypes (Bell 1982). The explanation favoured by many is the Red Queen model (Ebert & Hamilton 1996); but see the article by West (West et al. 1999). According to our model outcrossing is readily understood. In fact, the Red Queen model may be seen as one case of our model in that individuals being attacked by parasites may experience this as limitation of resources, because parasites draw on the resources taken up by the individual. This can initiate sexual reproduction, allowing to escape from the parasite by producing genetically different offspring experiencing less resource shortage.

Finally, let us extrapolate our findings to spatially extended systems. We consider the case that sexuals have the larger chance to win in each spatial region and that they are initially present in sufficiently many regions, such that they are not lost to demographic stochasticity. Since neighbouring regions are coupled through migration, sexuals can invade a region where the asexuals happened to win and take over also this region. The opposite may also happen but less frequently. If the number of regions is sufficiently large and time sufficiently long, the average number of regions occupied by sexuals will increase with time. We therefore conclude that in spatially extended systems there should exist a broad parameter region where asexuals will be almost non-existent. Preliminary computer simulations of a spatial model confirm this intuitive argument.