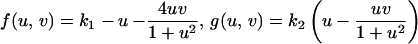Figure 8.
Transformation from juvenile to adult pigment markings in the angelfish P. semicirculatus, for a logistic-type growth. We use L1(t) = L2(t) = 
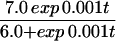
to model a domain growing exponentially initially and approaching a constant size at large time. Simulation results for the cell density show the slow insertion of new stripes as the domain grows during initial stages (a and b), followed by a breakup into a pattern of spots as the domain approaches its maximum size. During the breakup into spots, an intermediate phase can be seen where the pattern is a combination of stripes and spots (d and e). We use the Lengyel–Epstein model of the (chloride/iodide/malonic acid reaction for the chemical kinetics,
with parameter values k1 = 10.0, k2 = 17.6, Du = 0.01, Dv = 2.0, Dn = 5.0 ×10−5, χ0 = 2.5 × 10−5, and an initial domain of dimensions [0,1.58] × [0,1.58]. To force a pattern of regular stripes, we have selected initial conditions of the form shown in Fig. 6d for the morphogens.
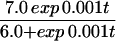to model a domain growing exponentially initially and approaching a constant size at large time. Simulation results for the cell density show the slow insertion of new stripes as the domain grows during initial stages (a and b), followed by a breakup into a pattern of spots as the domain approaches its maximum size. During the breakup into spots, an intermediate phase can be seen where the pattern is a combination of stripes and spots (d and e). We use the Lengyel–Epstein model of the (chloride/iodide/malonic acid reaction for the chemical kinetics,  |